基于无监督深度学习的线谱增强算法
鞠东豪,迟骋,李宇,张春华,黄海宁
(1. 中国科学院声学研究所,北京 100190;2. 中国科学院大学,北京 100039;3. 中国科学院先进水下信息技术重点实验室,北京 100190)
0 引 言
水下无人航行器由于平台体积小、能耗低以及无人等特点近年来被广泛应用于军民各个领域[1-2]。水下无人航行器搭载被动声呐探测水下目标也成为了近年来的一个研究课题。而对于被动声呐探测技术而言,往往关注接收信号中的低频线谱分量,这些线谱分量主要由于目标螺旋桨转动和内部的机械往复运动产生,并且线谱分量往往比接收信号中的宽带分量具有更高的功率和稳定性[3]。对于UUV 这样的小型平台而言,要提升对目标的检测性能,对这类线谱分量进行增强就显得尤为重要。
常规的自适应线谱增强器(ALE)已经被广泛地应用与被动声呐系统中[3-4],ALE 算法应用了线谱分量和宽带噪声分量之间的相关性差异进行线谱增强,是自适应滤波器的一个重要应用,除此之外ALE 算法还被广泛应用于语音校正以及生物医学信号处理等领域。在利用最小均方误差(LMS)迭代算法的线谱增强器中,由于存在迭代噪声,系统的增益和输入信噪比有关,当输入信噪比低于某一阈值时,系统增益迅速下降[4-5],因此,期望设计一种对输入信噪比有更强鲁棒性的线谱增强算法。
近年来深度学习算法在声学领域得到广泛的应用[6],但使用深度学习算法构建被动声呐的线谱增强器这一领域还未有人进行研究。本文尝试将深度学习算法应用于被动声呐线谱增强技术当中,提出基于无监督深度学习的线谱增强器。该方法同ALE 一样可以实时自适应的进行线谱增强,且不需要预先收集大量数据训练模型,相比较于传统的深度学习算法具有更强的环境鲁棒性。
仿真结果表明,本文提出的深度学习线谱增强器算法在输入信噪比为-30 dB 的情况下,该方法仍然可以实现约20 dB 的信噪比增益,这意味着本文算法可以更好地应用于被动声呐探测中,具有一定的优越性。
1 常规自适应线谱增强算法
1.1 信号模型
为简化分析,本文假设被动声呐接收信号由宽带白噪声分量和线谱分量构成,信号模型如下式:
其中: M 为线谱分量的个数; k 为时间索引; Ai, fi以及 φi分别为第i个线谱分量的幅度、频率以及初始相位;n(k)为宽带噪声分量。为了便于推导,本文假设M=1。
1.2 自适应线谱增强器
ALE 是一种自适应的窄带滤波器,ALE 算法可以从数据当中自动发现线谱所在的位置并增强线谱分量抑制宽带噪声分量,但常规的ALE 算法在低信噪比输入的情况下难以正常工作。本文主要介绍在极低输入信噪比条件下对线谱分量进行增强,选用常规ALE 算法作为参考算法,下面对常规ALE 算法及其输入信噪比限制进行描述。
常规ALE 算法的流程框图如图1 所示,常规ALE算法利用了线谱分量和宽带噪声分量在相关长度上的差异性进行线谱的增强。ALE 算法中使用了自适应滤波器,原始的输入信号x(k)作为自适应滤波器的参考输入。延时输入为x(k-Δ),其中 Δ表示延时的长度。
假设自适应滤波器抽头长度为 L,那么权值向量w可以表示为:
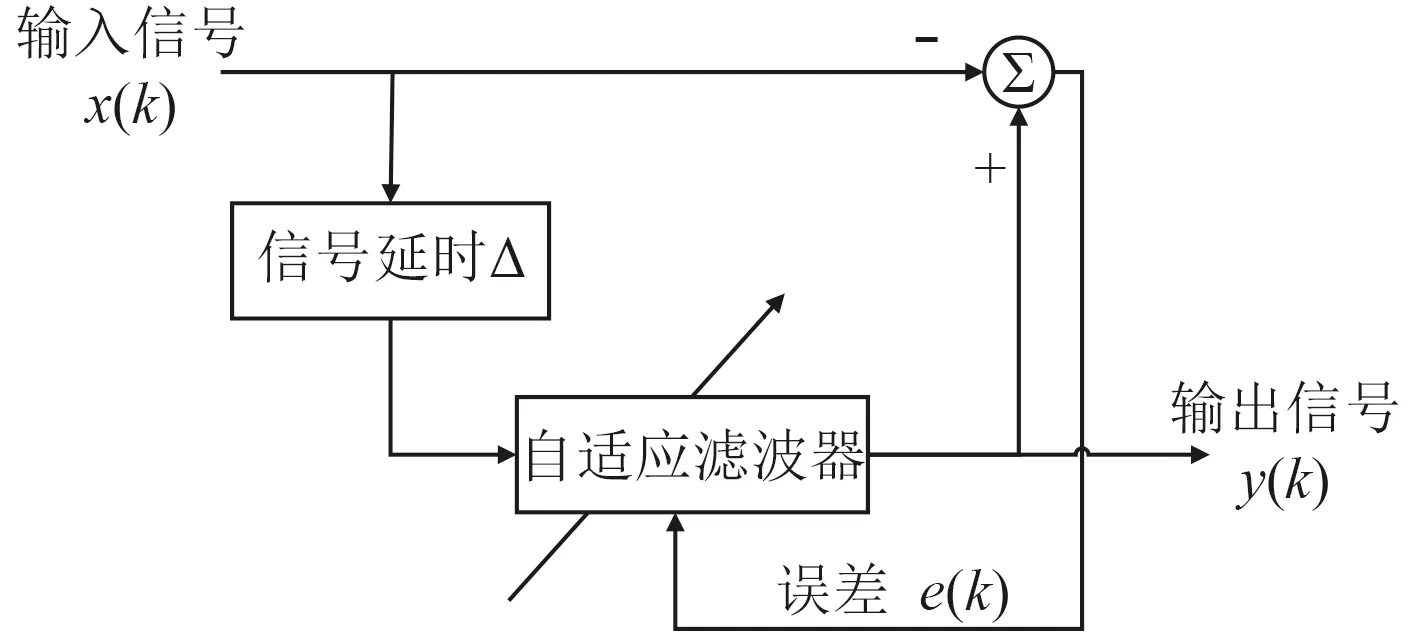
图 1 常规ALE 算法框图Fig. 1Schematic of the conventional ALE
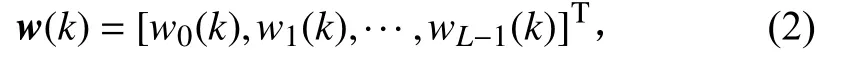
其中,[·]T为矩阵转置, k为时间索引。图1 中的输出信号 y (k),则可以通过式(3)得到:

LMS 算法是基于梯度下降算法,在LMS 自适应算法中,损失函数可以记为:
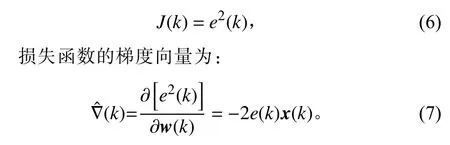
在LMS 自适应算法中,损失函数的梯度向量用于调整权重系数向量。ALE 中权重系数向量的更新公式可以表示为:
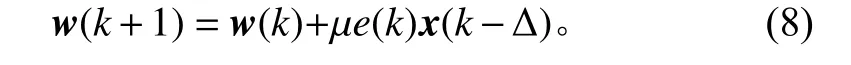
ALE 算法通过不断更新权值系数直至收敛,即可达到对线谱分量进行增强的目的。
与此同时有学者指出当ALE 的输入信噪比低于某个阈值时系统的增益会急剧下降。定义ALE 系统的信噪比增益 G(dB)为[6]:
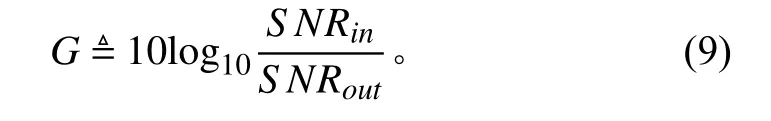
S NRin和 SNRout分别表示输入输出信噪比。当滤波器抽头长度L >>1时存在一个信噪比临界值[3]:
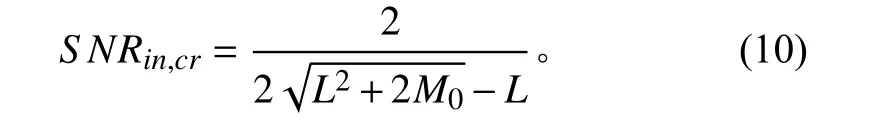
式中,M0=1/是以自适应周期为单位的迭代时间常数。
在水下微弱目标被动探测的应用中,被动声呐的接收信号信噪比可能会低于ALE 输入信噪比的最低要求,如何在极低信噪比下增强线谱信号已经成为被动探测领域不可忽视的一个问题。
2 基于无监督深度学习的线谱增强算法
ALE 利用了输入和延迟输入中只有线谱分量的输入是相似的这一特点,本文提出的无监督深度学习线谱增强算法同样也利用了输入和延迟输入之间的关系。受ALE 算法的启发,无监督深度学习线谱增强器算法使用延时输入来训练神经网络。在使用经过训练的神经网络进行线谱的增强,同传统的神经网络信号增强模型相比,本文所提出算法可以自适应的对线谱进行增强,并且可以实时处理数据,无需事先训练。同时与传统的ALE 算法相比,无监督深度学习线谱增强算法利用了神经网络的非线性能力,提升了系统在低输入信噪比下的增益。本文所提算法由训练和增强2 个步骤组成。
无监督深度学习线谱增强算法使用经过 x预处理后的数据x′(k)以及延时数据x′(k-Δ)作为训练数据,将神经网络模型的推测用函数形式表示为yˆ=h(x),最小化目标函数为:
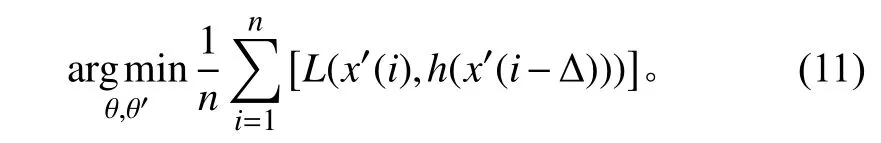
式中: θ, θ′表 示神经网络模型参数集合; n为输入层神经元个数; L表示目标函数,一般使用平方误差,即L(x,z)=‖x-z‖2。当输入到神经网络的数据量变大时,计算速度变慢。为了实现实时处理,选择小批量梯度下降法(Mini-batch Gradient Descent, MBGD)法来更新权值:
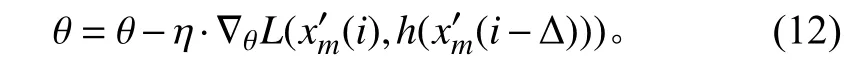
其中 η表示神经网络的学习率, xm表示第 m 批数据。通过上述方法对无监督深度学习线谱增强器模型进行训练,最终得到经过训练后的模型参数集 θ*, θ′*。再将经过预处理后的数据直接输入模型中,即可得到增强以后的数据,这一过程也等同于传统神经网络算法处理流程中的测试阶段,数学表达式如下式:
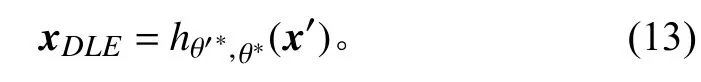
xDLE表示系统的输出结果。基于深度学习的线谱增强算法的实现流程如图2 所示。
无监督深度学习线谱增强器算法并不需要大量的数据进行模型的预先训练,同ALE 算法一样无监督深度学习线谱增强算法是在线对模型进行调优,因此线谱分量可以几乎实时的被增强。
3 实验与分析
3.1 仿真数据实验
仿真数据试验中使用式(1)中指出的信号模型,参数设定如表1 所示。
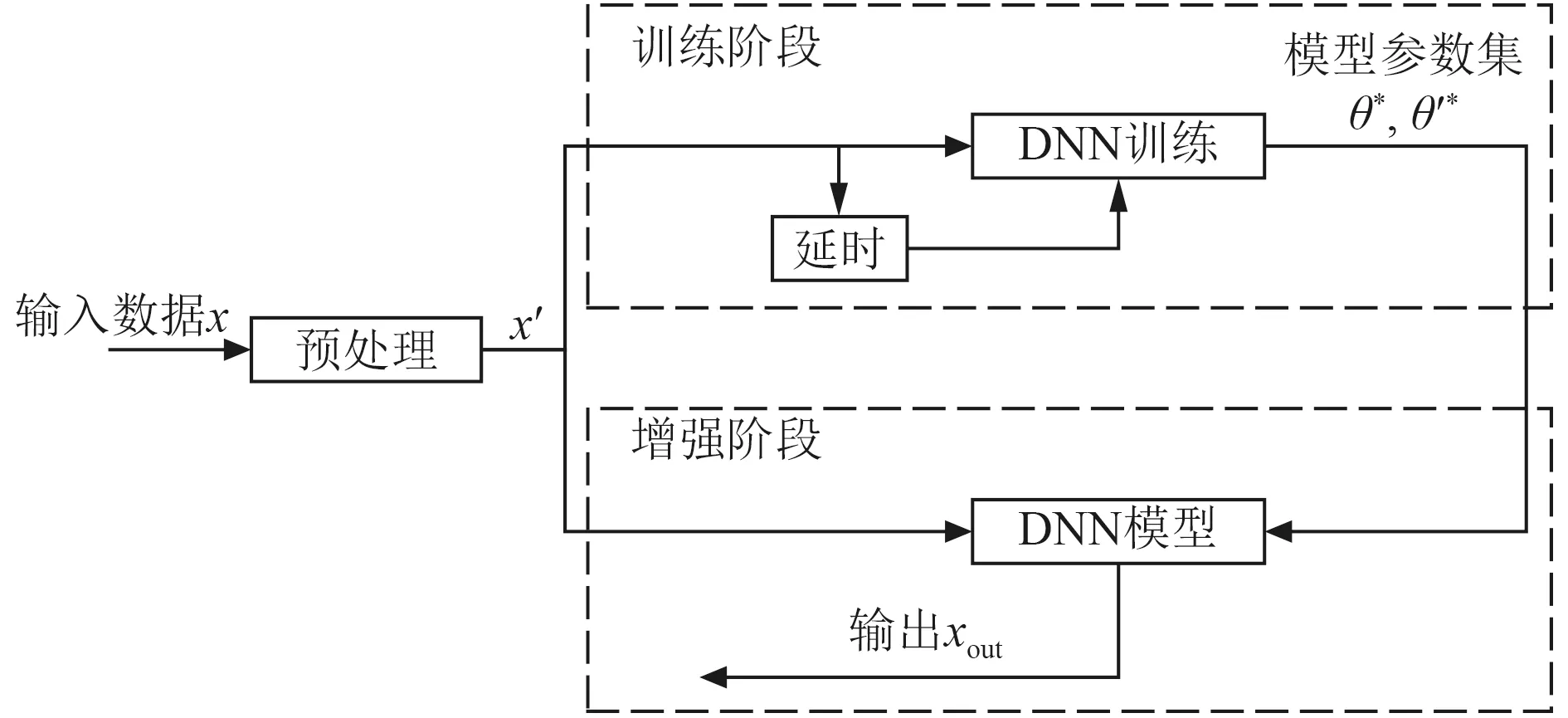
图 2 无监督深度学习线谱增强器算法框图Fig. 2Schematic of the proposed algorithm

表 1 仿真数据参数Tab. 1 Simulation data parameters
本文实验使用常规ALE 作为对比,ALE 及无监督深度学习线谱增强器算法参数如表2 和表3 所示。

表 2 ALE 算法参数Tab. 2 ALE algorithm parameters

表 3 无监督深度学习线谱增强器算法参数Tab. 3 ALE algorithm parameters
使用上述参数的2 种算法对比在低信噪比(-30 dB)情况下各自的线谱增强结果,如图3 所示。
对比2 种方法的处理结果,从图3(b)可以看出,当信噪比为-30 dB 时,在LOFAR 谱中难以观察到线谱的存在。对于传统ALE,图3(c)显示300 Hz处的线谱几乎没有增益。而对于本文提出的无监督深度学习线谱增强器算法,可以在图3(d)中清晰地看到300 Hz 处的线谱分量。
3.2 实际数据实验
为了更好地验证本文所提出的无监督深度学习线谱增强器算法,于渤海使用水下无人航行器舷侧阵采集水面合作渔船辐射噪声数据进行线谱增强实验。为了验证在低信噪比情况下的算法性能,在原有数据基础上加入了10 dB 宽带噪声。实际数据采样率为10 kHz,算法参数同表2 和表3,处理结果如图4 所示。
从图4 可以看出,2 种方法在应用于实际数据时都具有增强音调的能力。传统ALE 算法对53 Hz 处的线谱有较好的增强效果,但对于低信噪比的线谱,如300 Hz 处的线谱增强效果较差,对不可见的线谱难以增强。而无监督深度学习线谱增强器算法对310 Hz,320 Hz,340 Hz 甚至更低信噪比的线谱都有增强效果。
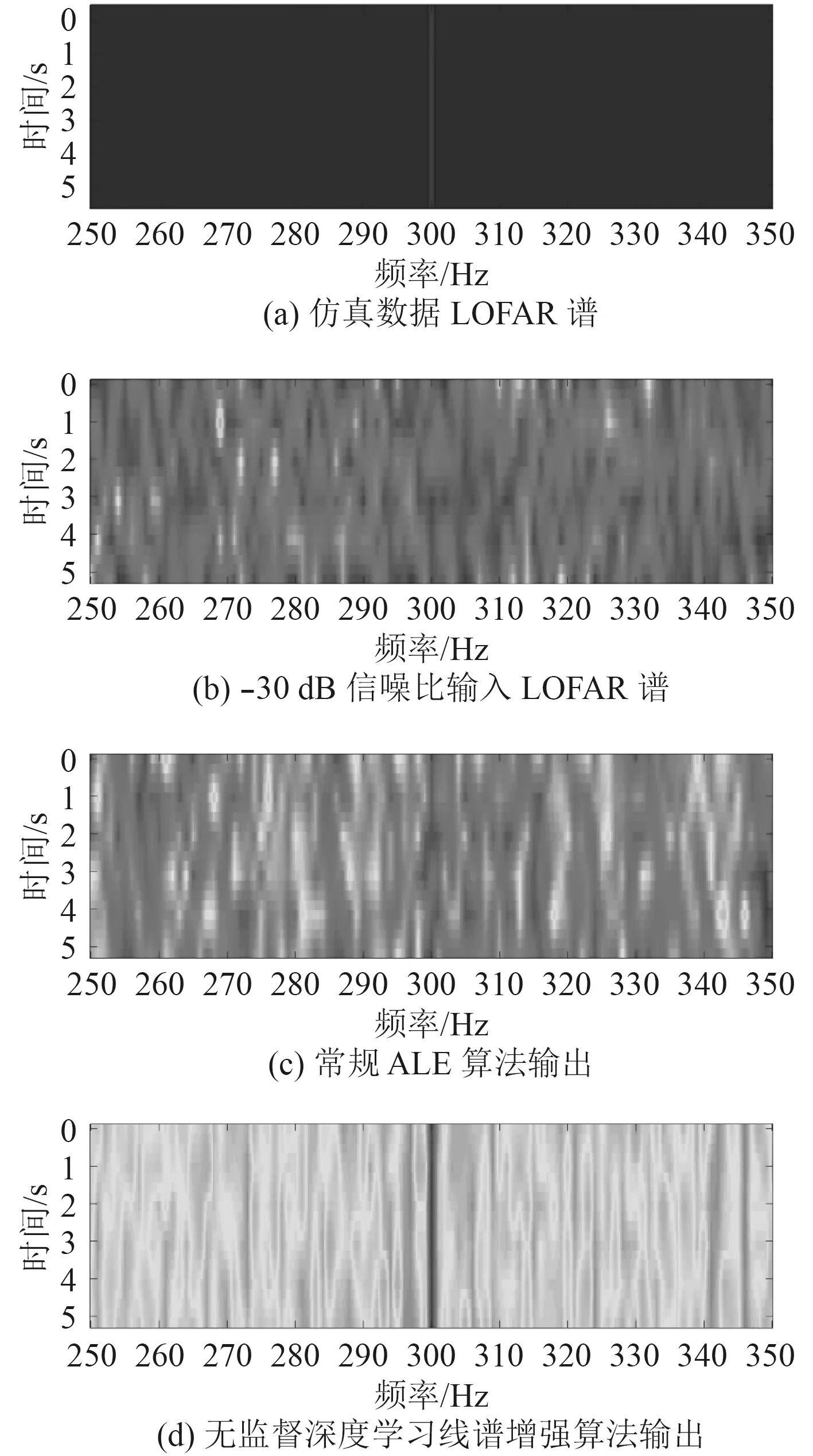
图 3 两种方法线谱增强结果Fig. 3LOFAR of two mathods
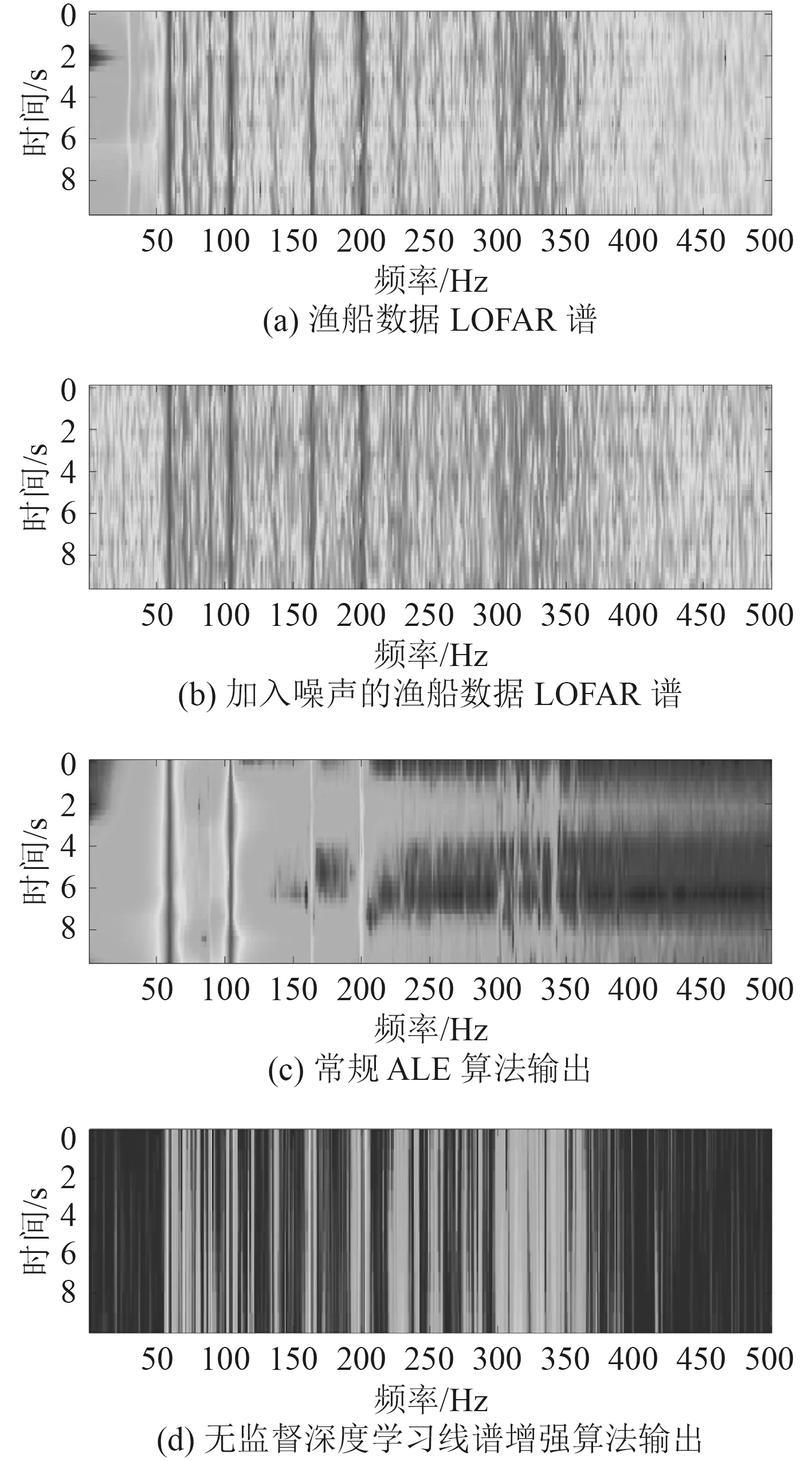
图 4 两种方法的处理结果Fig. 4The lofargrams of two mathods
4 结 语
本文受到了传统ALE 算法的启发,利用神经网络较强的非线性能力提出一种基于深度学习的线谱增强算法。仿真实验表明,无监督深度学习线谱增强算法能显著提高信噪比增益,当信噪比低于-30dB 时,无监督深度学习线谱增强器算法仍能获得较高的增益,而ALE 算法很难获得增益。实验表明,无监督深度学习线谱增强器算法可以增强低信噪比的线谱成分。与传统ALE 算法相比,本文提出的无监督深度学习线谱增强算法在低信噪比条件下具有更好的增强效果。本文所提算法可应用于无人航行器搭载的被动声呐,提高其探测性能。

