基于钟差预测的铯原子钟频率异常检测算法及性能分析

伍贻威

北京卫星导航中心，北京 100094

守时试验室和全球导航卫星系统(GNSS)都需要利用多台原子钟组成钟组，建立和保持一个时间基准[1-4]。守时本质上是个预测问题，即需要通过原子钟的历史表现来预测其未来表现[5-8]。国际上已经达成共识[8]：一个好的钟应该是一个可预测的钟(a good clock is a predictable clock)。可预测性的一个重要体现是原子钟信号没有异常[8]。建立一个实时的、可预测的纸面时间，需要在异常发生后尽可能短的时间内检测出异常；根据异常的严重等级，合理降低其权重甚至剔除出钟组，尽可能降低异常对于纸面时间的影响[8]。

频率异常检测的性能是与原子钟的噪声水平高度相关的。典型氢钟的闪烁底(flicker floor，即Allan偏差最小值)一般在10-15～10-16量级，而典型铯钟的闪烁底只能达到10-14～10-15量级。这就导致相对于氢钟，铯钟10-14量级的频率异常可能淹没在噪声之中，从而更不容易检测，因而其对纸面时间的影响也更大。

国内外检测频率异常的研究方法包括：动态Allan方差法[9-11]、时-频谱分析法[9,12]、假设检验法[11,13-16]。动态Allan方差法对微小频率异常的反应时间较长；时-频谱分析法比较适用于检测时变信号或是周期性波动等在频谱上出现明显谱线的异常；假设检验法较适用于频率异常的检测。

假设检验法的核心是设计合理的检验统计量和相应的检测门限值。检测门限值是由检验统计量的统计特性以及虚警概率(PFA)决定的。进一步，可以推导出检测概率(PD)和PFA、平均频率跳变幅度(|Ya|)之间的函数关系。一般认为检验统计量的统计特性是先验已知的，这在大部分情况下都是可行的。因为对于某一台原子钟，其噪声的统计特性一般不会发生很大的改变。当检验统计量的统计特性未知，可以采用广义似然比(generalized likelihood ratio test，GLRT)的方法，在检验统计量的分布函数中用最大似然估计结果代替未知参数。因此，GLRT法[11]可以看成是假设检验法的特例。

目前的研究中，文献[13]只分析了不同PFA的试验效果，也就是只进行了第一步，没有从理论上进一步推导不同|Ya|对应的PD；包括采用GLRT法在内的大部分假设检验法的检验统计量都是频差[11,14-16]，例如文献[14—15]采用的检验统计量分别为Kalman滤波器输出的频差的一步和多步预测误差，没有充分利用频率异常在时差上的积累效应。

本文基于文献[17—18]等描述的典型铯钟的钟差预测不确定度的解析表达式，将时差的预测误差作为检验统计量，这一点与文献[11，14—16]有所不同。本文认为原子钟的噪声特性可以先验得到，所以在算法中是已知的，不需要再采用GLRT法来估计参数。进一步，按照文献[19—20]的思路，结合预测误差的概率分布函数，推导了不同PFA对应的检测门限和PD的计算公式，并总结了提高PD的方法。根据本文的理论分析结论，只要给出PFA和|Ya|的值，即可计算得到PD，这为铯原子钟的频率异常检测提供了理论支撑。后续还可以将本文算法的性能与大部分采用频差作为检验统计量的算法[11,14-16]进行对比分析，进一步优化算法设计。

1 基本原理

1.1 原子钟信号

典型铯钟的时差表示为[21-24]

X1(t)=x0+y0t+σ1W1(t)+

(1)

式中，等号右侧前2项为一次多项式表示的确定性分量，后2项为随机性分量，即原子钟噪声；X1代表原子钟时差；x0和y0分别代表时差和频差的初值；W1(t)和W2(t)分别代表2个独立的维纳过程，并且有W(t)～N(0,t)，即每个维纳过程服从数学期望为0，方差为时间t的正态分布；σ1和σ2分别是这2个维纳过程的扩散系数(diffusion coefficients)，用于表明噪声的强度；第3项代表调频白噪声(white frequency modulation noise，WFM)；第4项代表调频随机游走噪声(walk random frequency modulation noise，RWFM)，即W1(t)、W2(t)的积分在X1上分别表现为WFM和RWFM。

WFM和RWFM都是有色噪声[25]，一般采用Allan方差来表征频率稳定度[26]。Allan方差表达式为[21-23]

(2)

式中，τ为平滑时间。式(2)等号右侧第1项为WFM分量，第2项为RWFM分量，表明WFM和RWFM在对数Allan方差图中的斜率分别为-1和1。

式(1)中的原子钟噪声服从正态分布，数学期望为0，方差为[19,21]

(3)

式中，等号右侧第1项是WFM的方差；第2项是RWFM的方差，它们都随时间的变大而变大。观察式(2)和式(3)，得到

(4)

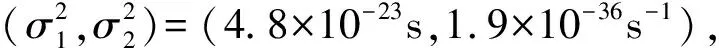
图1展示了这100台仿真铯钟的时差(绿色曲线)，以及式(3)的1倍和2倍平方根计算得到的1σ和2σ噪声标准差(黑色加粗曲线)。从图1清楚地看出噪声标准差随时间的变大而变大。

1.2 钟差预测基本原理

观测钟差可以认为是时差叠加上观测噪声，表示为[17-18]

Z(tk)=X1(tk)+σ·ξ(tk)

(5)

式中，Z(tk)是在tk时刻的观测钟差；ξ(tk)是在tk时刻的观测噪声，一般认为是调相白噪声(white phase modulation noise，WPM)；σ代表观测噪声的强度。

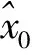
(6)

预测误差由[预测值-真实值]来表示。由式(1)和式(6)，预测误差表示为

(7)

(8)

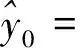
[W1(t0)-W1(t0-T)]+

(9)

维纳过程具有以下性质

cov[W(s),W(t)]=min(s,t)

当t≥s时

式中，cov代表协方差；min代表最小值。当t=s时，协方差实际上就是方差。

根据维纳过程和白噪声的性质，推导得到

(10)

(11)

(12)

于是得到

(13)

同理，根据维纳过程的性质，推导得到

(14)

(15)

将式(13)—(15)代入式(8)，得到

(16)

预测不确定度u(tp)为式(16)的平方根。1σ预测不确定度和2σ预测不确定度从统计意义上分别代表了预测误差的68%和95%的置信区间。

1.3 观测间隔选取

本地的钟差测量不确定度可做到优于0.1 ns(σ2=1×10-20s2)，当预测时间tp不是太短时，其影响基本可以忽略。假设σ2=0，将式(2)代入式(16)，得到

(17)

式中，u2(tp)包含2项；对于给定的tp，第2项的值不变；当选择观测间隔T等于Allan方差曲线(一般为V字形)取最小值对应的平滑时间值(记为Tmin)时，第1项取最小值，于是u2(tp)取最小值。对于与图1相同参数的典型铯钟，使第1项取最小值的T约等于100 d。

图1 100台仿真铯钟的时差、1σ和2σ噪声标准差Fig.1 Time differences and 1σ and 2σ noise standard deviation of the 100 simulated cesium clocks

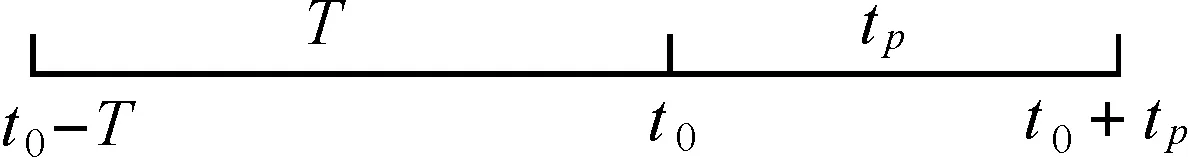
图2 钟差预测Fig.2 Diagram of clock prediction

从图3得出结论：预测时间较短即当tp≪T时，u(tp)仅略大于σy(tp)tp；这时预测性能主要由原子钟噪声决定。

从直观上理解：假设时差和频差的估计误差都一直为零，这相当于估计值与真实值完全相同(实际上是不可能的)，此时按照式(7)，如果忽略观测噪声，预测误差完全就是原子钟噪声，噪声方差随时间变大，如图1所示。

图3 预测不确定度及其前3项和第4项平方根的值Fig.3 Prediction uncertainty and its first three terms and the fourth term values

表1 不同T和tp对应的u(tp)

从表1可以看出，当tp≪T且T≤Tmin时，u(tp)仅略大于σy(tp)tp。

2 频率异常检测算法

2.1 基本思路

通过对比分析预测误差和预测不确定度，提供了一种检测原子钟频率异常检测的方法[19]，即当异常发生在未来时间段[t0,t0+tp]时，在某个t时刻(t>t0)及之后时间段的预测误差一直大于某个门限值，认为在t时刻频率发生了跳变。

本节首先选取门限值等于3σ预测不确定度的理论值为示例进行说明，再推广到一般情况。预测误差落在±1σ、±2σ和±3σ预测不确定度范围内的理论概率分别为68.26%、95.44%和99.74%[28]。从理论上讲，预测误差大于3σ预测不确定度的概率很小，仅为1-99.74%=0.26%。

2.2 频率跳变检测方法

本文方法等价于做如下二元假设检验。

H0——未发生频率跳变。

H1——发生频率跳变。

选取预测误差ε(tp)作为检验统计量。首先需要确定在这两种假设下，检验统计量的数学分布。

H0情况下，显然预测误差服从N(0,u2(tp))分布。

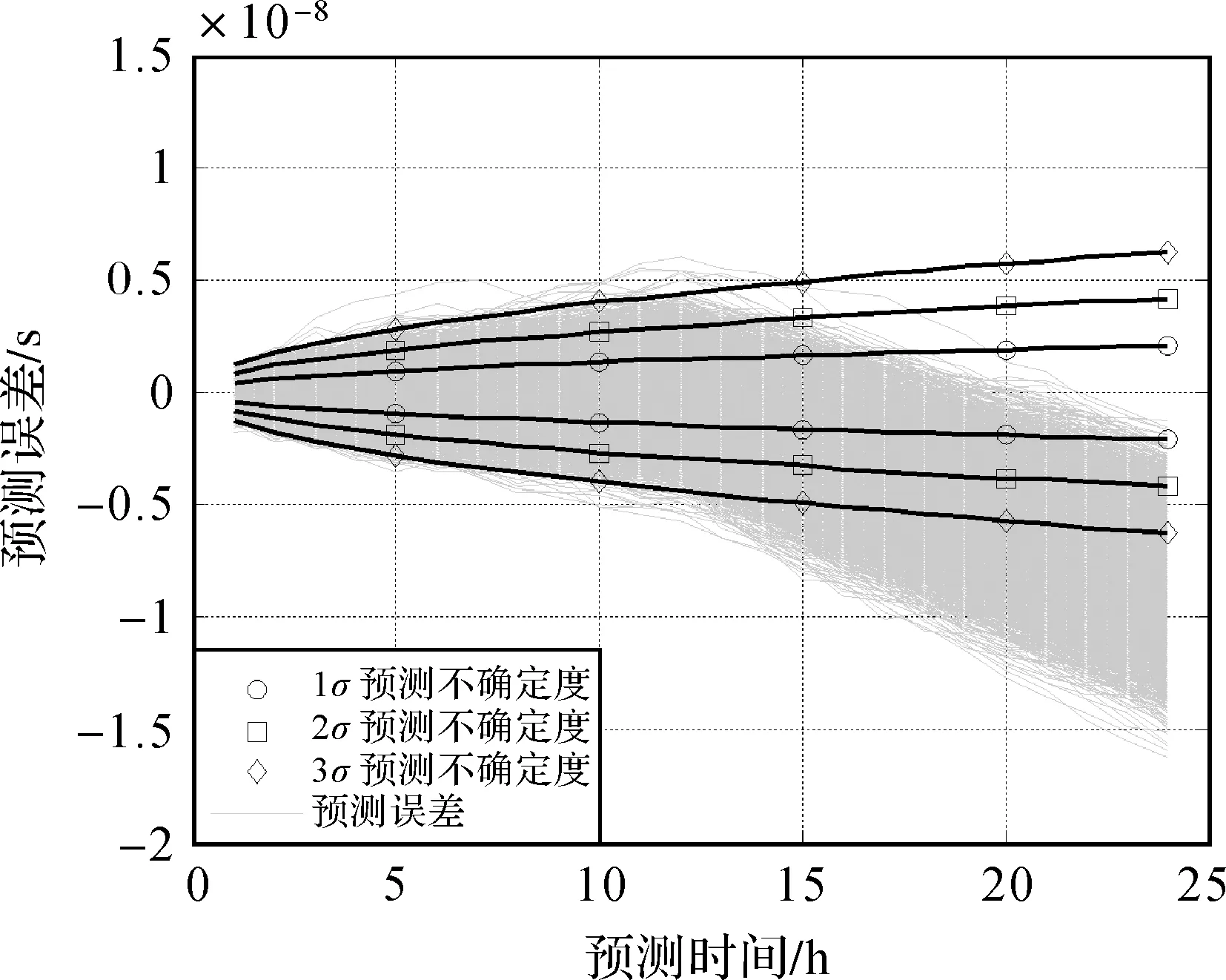
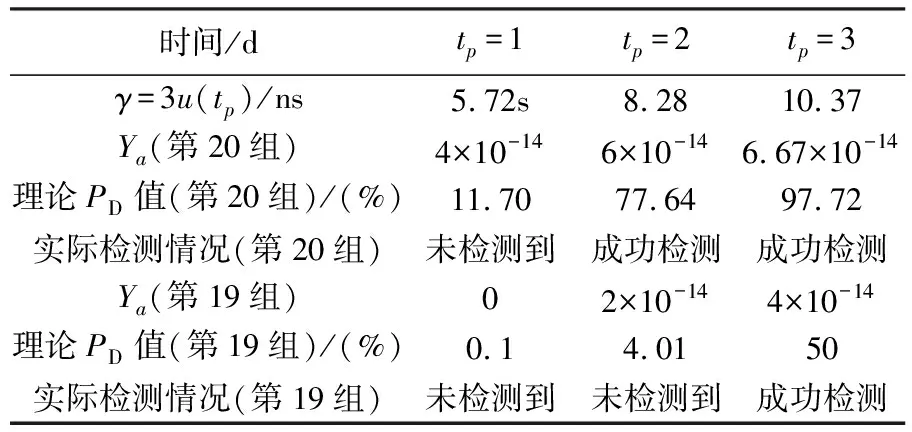
H1情况下，假设跳变发生在[t0,t0+tp]的中间时刻，记为t0+tp-Tjump时刻，其中0

(18)

所以，在[t0,t0+tp]时间段内积累的时差为

xjump(T)=Yatp=Y0Tjump

(19)

这时预测误差服从N(Yatp,u2(tp))分布。

综上，在这两种假设下统计量的数学分布为

(20)

将H0为真时判H1成立的概率称为虚警概率，用PFA表示[25]。把H1为真时判H1成立的概率称为检测概率，用PD表示[25]。PFA的值也被称为显著性水平[28]。

本文通过约束PFA，求解不同Ya对应的PD。

如前文所述，ε(tp)落在±u(tp)、±2u(tp)和±3u(tp)范围内的概率分别为68.26%、95.44%和99.74%，对应的PFA分别为1-68.26%=31.74%、1-95.44%=4.56%和1-99.74%=0.26%[28]。

以约束PFA=0.26%为例。直观上理解，假如|Ya|tp=3u(tp)，显然有PD=50%；那么当|Ya|tp>3u(tp)时，PD>50%；当|Ya|tp<3u(tp)时，PD<50%。因此，当约束PFA时，PD是与|Ya|正相关的；|Ya|越大，PD越大。

具体而言，以约束PFA=0.26%为例，根据式(20)，推导出检测概率的表达式为

(21)

由式(21)可以求解得到任意Ya对应的PD。

2.3 示例分析和更一般的情况

从图4中看出，PD随着|Ya|的增大而增大；当|Ya|=3u(tp)/tp=7.26×10-14时，PD=50%(图中圆圈)，即直观认识与式(21)计算结果是符合的。

服从标准正态分布的随机变量X的分布函数用φ(x)来表示[28]。几个关键数值为φ(-3)=0.001 3，φ(-2)=0.022 8，φ(-1)=0.158 7，φ(0)=0.5，φ(1)=0.841 3，φ(2)=0.977 2，φ(3)=0.998 7[28]。

图4 PD-|Ya|曲线Fig.4 PD-|Ya| curve

前文所述的“ε(tp)落在±u(tp)、±2u(tp)和±3u(tp)范围内的概率分别为68.26%、95.44%和99.74%”，对应于φ(1)-φ(-1)=68.26%、φ(2)-φ(-2)=95.44%和φ(3)-φ(-3)=99.74%[28]。

显然，在H1情况下，统计量ε(tp)的分布函数为

(22)

所以，对于该实例，在约束PFA=0.26%时，不同|Ya|对应的PD如表2所示。

表2 不同|Ya|对应的PD

由图4和表2看出：当|Ya|>4u(tp)/tp时，可以比较有效地检测出异常；当|Ya|>1.05×10-13时，检测概率在90%以上；当|Ya|较小(例如<3u(tp)/tp)时，检测效果并不显著。

上述示例中约束PFA=0.26%，对应的ε(tp)门限值为±3u(tp)。在更一般的情况下，可以约束PFA=5%、PFA=1%、PFA=0.1%等。这时，对应的ε(tp)门限值±γ需要查询分布函数φ(x)的函数表来确定，具体方式是使φ(γ)-φ(-γ)=1-PFA。例如，当约束PFA=5%时，查阅φ(x)的函数表，得到γ=1.96u(tp)。然后，需要将式(21)中积分下限(上式)或上限(下式)分别修改为γ和-γ，得到式(23)。根据式(23)，可以求解得到任意幅度|Ya|对应的PD值。

(23)

3 仿真分析、实测数据分析

3.1 仿真分析

图5和图6分别给出了在Ya=3u(tp)/tp和4u(tp)/tp的情况下时，两次各10 000台铯钟的预测误差ε(tp)。从图5和图6中明显看出在t0+tp/2时刻发生的频率跳变。

分别统计在这两种情况下ε(tp)落在±3u(tp)外的铯钟数量，作为本文方法检测出频率跳变异常的数量。在这两种情况下，能检测出频率跳变异常的数量分别为5067台和8502台。

表3列出了在这两种情况下，理论PD值、实际检测数量和相应的试验PD值。

图5 Ya=3u(tp)/tp时10 000台铯钟的预测误差Fig.5 Prediction errors of 10 000 cesium clocks when Ya=3u(tp)/tp

图6 Ya=4u(tp)/tp时10 000台铯钟的预测误差Fig.6 Prediction errors of 10 000 cesium clocks when Ya=4u(tp)/tp

表3说明，试验PD值和理论PD值基本符合。

综上，仿真试验验证了理论分析的结论。

表3 不同Ya对应的理论和试验PD值

3.2 实测数据分析

图7 铯钟钟差和钟差的一次多项式残差Fig.7 Cesium clock difference and its one-order residual

人为在第39.5 d处引入幅度为8×10-14的频率跳变。共进行20次预测，都选取T=20 d和tp=3 d。第1次预测从第20 d开始，之后每次预测开始时间往后移1 d，最后1次预测开始时间为第39 d。共获得20组预测误差曲线。选取γ=3u(tp)，即约束PFA=0.26%。

图8给出了这20组预测误差曲线以及3σ预测不确定度曲线，其中第20组为红色(当tp等于1 d、2 d和3 d时标注圆圈)，第19组为蓝色(当tp等于1 d、2 d和3 d时标注方块)，其余18组为绿色。从图8看出：对于第20组，相当于在tp=0.5 d时发生了异常，当tp=1 d时未检测出异常，tp=2 d和tp=3 d时成功检测出了异常；对于第19次预测，相当于在tp=1.5 d时发生了异常，当tp=2 d时未检测出异常，当tp=3 d时成功检测出了异常。

图8 20组预测误差曲线以及3σ预测不确定度曲线Fig.8 20 prediction error curves and 3σ prediction uncertainty curve

表4列出了对于第20组和第19组，当tp分别等于1 d、2 d和3 d时，按照式(16)计算得到的γ、按照式(18)计算得到的Ya、按照式(23)计算得到的理论PD值、实际检测情况(图8)。

表4 不同Ya对应的理论PD值和检测情况

综上，实测数据试验验证了理论分析的结论。根据本文的理论分析和仿真试验，还可以进一步得到以下结论。

(1)PD和PFA、|Ya|之间存在函数关系，约束PFA、|Ya|之中任意一个量的值，可以得到PD和另一个量的函数曲线。

图4给出了PD-|Ya|曲线。实际上，当约束|Ya|时，还可以画出PD-PFA曲线，这就是著名的接收机工作特性(receiver operating characteristic，ROC)曲线，分析在不同|Ya|情况下不同PFA值对应的PD值，可以更合理地选取PFA的值。

(2) 根据ROC曲线，对于相同的|Ya|，假如PFA值更大，相应的PD也更大。

例如，当T=20 d和tp=1 d时，根据表2，假如将PFA值由0.26%提高至4.56%，相当于将检测门限γ由±3u(tp)降低至±2u(tp)，原来|Ya|=3u(tp)/tp=7.26×10-14时，才有PD=50%，现在只需要|Ya|=2u(tp)/tp=4.84×10-14时，就有PD=50%，而当|Ya|依然为3u(tp)/tp=7.26×10-14时，PD=84.13%。

(3) 当tp≪T且T≤Tmin时，对于相同的PFA，假设|Ya|保持不变，增加tp，可以有效增大PD。

例如：当T=20 d，约束PFA=0.26%时，如果tp=1 d，当Ya=3u(1 d)/1 d=7.26×10-14时，有PD=50%；如果tp=2 d，当Ya依然为7.26×10-14时，根据式(21)计算，有PD=87.36%；如果tp=2 d，此时只要Ya=3u(2 d)/2 d=5.26×10-14，即有PD=50%。从直观上理解：预测时间tp越长，由频率跳变引起的积累时差越大，即式(20)中的|Ya|tp变大，所以PD增大。

(4) 进一步，当tp≪T且T≤Tmin时，对于同样的Y0，增加tp，使得|Ya|也相应地变大，|Ya|和tp同时增大使PD增大的效果更显著。

例如，依然采用上述情况，假设在t0+12 h时刻发生频率跳变，幅度为Y0=6u(1 d)/1 d=1.45×10-13，如果tp=1 d，按照(18)计算得到Ya=Y0/2=7.26×10-14，这时根据式(21)计算，有PD=50%；如果tp=2 d，按照(18)计算得到Ya=3Y0/4=1.14×10-13，这时根据式(21)计算，有PD=99.93%，即基本可以检测出异常。所以，对于同样的Y0，增加tp，相当于使式(20)中的|Ya|和tp都增大，所以|Ya|tp将变得更大，从而PD更高。

4 结束语

本文提出一种基于钟差预测的铯原子钟频率异常的检测算法。本算法采用假设检验的方法，检测概率(PD)和虚警概率(PFA)、平均频率跳变幅度(|Ya|)之间存在函数关系。为了充分利用频率异常体现在时差上的积累效应，本算法将时差的预测误差作为检验统计量，对检验统计量做二元假设检验。在两种情况下，检验统计量都服从正态分布。通过约束PFA，查询正态分布的分布函数，得到对应的检测门限值。根据在异常情况下的检验统计量分布函数和检测门限值，推导给出了求解|Ya|对应的PD的表达式。仿真试验和实测数据试验都验证了理论分析的结论。

在实际应用中，由于算法已经约束了PFA，一旦算法给出报警，那么极有可能发生了频率异常(发生异常的概率为1-PFA)，此时需要进行人工干预。|Ya|越大，PD也就越高。根据本文的分析结论，提高PD的方法有：①提高PFA(相当于降低γ，尽管会增加系统报警的频度)；②增加tp(当tp≪T且T≤Tmin时，相当于同时增大了|Ya|和tp)。本文成果还可以应用于精密定轨与时间同步领域[29]。