基于灰色系统及BP神经网络算法的边坡变形预测精确度影响分析

姜永杰 张书豪 吴 光 张广泽 柴春阳

(1.西南交通大学， 成都 611756；2 中铁二院工程集团有限责任公司， 成都 610031)

自然状态下边坡变形受到降雨、地震以及人为活动等因素的影响，边坡位移的大小及变形速度均难以预测。但随着数据处理理论以及计算机技术的不断进步，对已获取的变形数据处理方法的选择也逐渐成为影响边坡变形预测的重要影响因素之一[1-3]。如王万详[4]基于Kalman滤波的灰色神经网络，在短期预测中，充分利用Kalman滤波动态实时产生新的最优估计值去除噪声干扰，并使用BP神经网络模拟GM(1,1)预测结果的残差序列，重构GM(1,1)的预测值，达到了较好的预测精度。马文涛[5]等人研究的基于小波变换和GALSSVM边坡位移预测模型，利用互信息法和伪邻近法对小波变换的高低频信号分别进行相空间重构，以此获得有较高预测精度的位移值。

由此可见，基于不同预处理方法的预测模型，在针对不同特性的边坡数据时各有所长。目前，研究边坡变形的算法层出不穷，而探索窗口平移多项式、小波分析、灰色系统GM(1,1)、BP神经网络等常见算法之间影响的分析课题少之又少。因此，本文采用MATLAB软件，通过算法耦合，构建基于不同预处理工具的预测分析模型，并以标准差及相关性系数作为检测标准，探索各算法间的最佳耦合方式。

1 耦合算法及精度评价参数选取

为探究边坡变形分析中常见的数据预处理算法对变形预测精确度的影响，本文采用已通过精密测量获取的云南某桥岸边坡变形数据，并利用该边坡前期状态稳定，后期因两次隧道施工位移变形急速增大，最终又趋向稳定的变形特征，同时利用其累计位移量先直线抬升，后两次曲线上升至稳定的位移时序图，在MATLAB程序中构造基于最小二乘的三阶窗口平移多项式拟合法、小波分析、灰色系统GM(1,1)、BP神经网络的两种边坡数据预处理方法和两种数据预测模型。然后进行两两耦合，获得基于窗口多项式平滑的灰色系统、基于窗口多项式平滑的BP网络模型、基于小波分析的灰色系统和基于小波分析的BP网络模型四种边坡数据处理模型，探索函数搭配在边坡位移时序图中直线段预测及曲线段预测中的表现，同时以标准差及相关性系数数值作为位移预测值校验标准，推荐边坡变形不同趋势下的最优算法组合。

2 研究方法

2.1 数据预处理工具

2.1.1窗口平移多项式

(1)

若使残差最小，则ε对各个参数的偏导数应为0，化简为：

(2)

得到ak值，便可求出该组数据的拟合多项式表达式。演绎推理后得知，若将数据平分为多组，便可以2M+1为窗口维度进行移动式平滑处理。

2.1.2小波分析

小波分析是20世纪80年代中后期发展起来的新兴学科，其基本思想是用一族函数去表示或逼近另一信号或函数。该族函数可称为小波函数系，其表达式由基本小波函数平移和伸缩构成[7-8]。

(3)

对监测数据信号进行小波分解，实质是将信号分解为带有噪音的高频部分和带有监测信号特征的低频部分，如式(4)所示。

(4)

hn和gn为一对共轭镜像滤波器的脉冲响应，分别为低通滤波器H和高通滤波器G的滤波器系数。对分离出来的高频信号再逐次进行分解，直到高频噪音被大规模分离。最终将所有分离出来的低频信号进行重构，得到较为真实的监测信号。

2.2 数据预测工具

2.2.1灰色系统

灰色系统是对规律信息不明确的系统进行信息挖掘的方法，通过前期对数据的累加累减，将数据内部的灰度关联及积分特性进一步显现，由于新生成的数据呈现近似指数增长规律，可由一阶微分方程表示[9-10]：

(5)

进而利用最小二乘法求解，得到时间响应序列表达式：

(6)

进而完成以微分方程代替差分方程累减逆推得到新数据，得到GM(1,1)预测模型表达式。在单调数据的短期预测中有良好表现。

(7)

2.2.2BP神经网络

BP神经网络为多层前馈网络，其核心理论在于设置输入层、隐含层以及输出层，其预测输出值O由式(8)计算得出[11]。

(8)

式中：Hj——J层隐含层输出值；

wjk——连接权值；

b——隐含层阈值。

数据在各层之间的传递权重及隐含层的阈值均可依据输出值O与期望数值的差异进行调整。

ek=Yk-Ok(k=1,2,3,…,m)

(9)

(10)

(11)

式中：ek——网络预测误差；

η——学习速率。

不断“学习”减少差异直到达到误差要求，因此神经网络的模拟过程相当于大脑对一组含有特定规律数据的“认知过程”。

在灰色系统及BP神经网络的运用中，发现两种预测模型都具有“样本学习”的处理过程，由此可推知，不同的学习样本必然会对各自模型的预测结果产生影响。因此，本文结合自然状态下边坡的变形数据，将数据预处理、数据预测两类功能不同的方法两两耦合共生成四种方法组。四种方法模型既可横向比较判断前期预处理方法对预测结果精确度的影响，又可纵向比较判断在边坡变形数字化分析中处理结果贴合实测值的最优搭配。

3 工程运用

云南某桥岸边坡具有典型的高山峡谷坡面特性，自施工以来布设的自动监测装置已获得了桥岸边坡长时期的变形时序图。为充分展示各方法组的预测性能，特遴选具有前期缓慢抬升，后期两组曲线波动直至稳定的监测数据。数据采集时间由2016年11月16日始，至2017年11月13日结束。采集周期为2 h/d。其中3月31日和7月17日分别开始左右隧道锚施工爆破，因此位移时序图呈阶跃式抬升。边坡变形时序图总趋势及各部分分段利用方式如图1所示。

图1 某岸边坡2017年变形位移时序图

由图1可以看出，在MATLAB中对直线段-1区域采用窗口平移多项式和小波分析进行平滑降噪处理，两种方法得到的结果皆用来作为灰色系统和BP神经网络预测直线段-2区域的学习样本，并以直线段-2区域原数值进行参照，通过标准差和相关性系数作为预测结果精确度的检验标准。曲线段的研究过程与直线段相同。标准差和相关性系数数值可体现出不同方法组在处理不同特征曲线时的实用性。

3.1 直线段区域的平滑处理与预测

在MATLAB中，窗口平移多项式与小波分析对直线段-1区域的平滑处理结果分别如图2、图3所示，直线段-1原始观测位移时序图如图3所示。

图2 直线段-1 窗口平移多项式拟合结果图

图3 直线段-1 小波分析拟合结果图

图4 直线段-1原始观测位移时序图

两者平滑处理结果与原数据对照的标准差和相关性系数如表1所示。

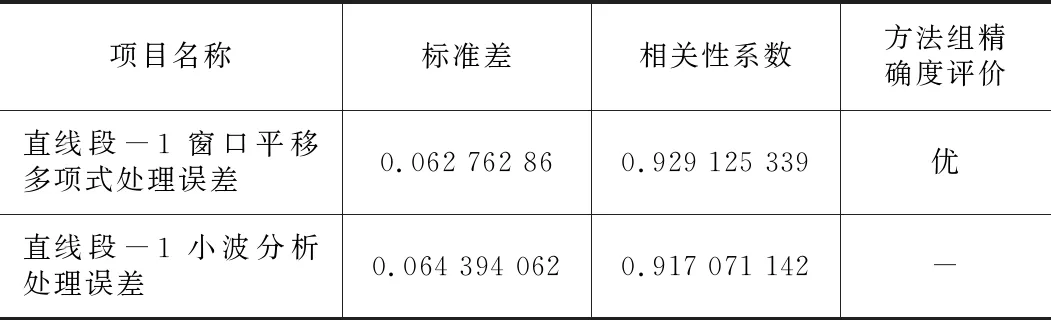
表1 直线段-1预测误差分析表

灰色系统分别采用窗口平移多项式及小波分析的处理结果作为学习样本时，直线段区域学习及预测的总过程如图5、图6所示。

图5 直线段中灰色系统GM(1,1)基于窗口平移多项式的学习预测总过程图

图6 直线段中灰色系统GM(1,1)基于小波分析的学习预测总过程图

两种预测结果与原数据对照的标准差和相关性系数如表2所示。

表2 直线段-2灰色系统GM(1,1)预测误差分析表

由图5、图6可以看出，无论采用哪种平滑方法的结果作为学习样本，灰色系统的预测曲线走向与原始数据均相差较大，这是因为灰色系统的核心计算思想是通过对学习样本的累加处理，使原始数据内在的指数函数特性得以显现，直线段-1区域的数据具有较强的指数特性，但观察直线段-2区域的数据并不符合直线段-1区域数据的指数特性。因此预测数据与对照组数据大相径庭。同时，在灰色系统的理论计算中，逆推阶段的初始值并由微分方程的解累减获得的，而是直接采用的原始数据初始值，微分方程的解是基于最小二乘法获得的，在计算过程中考虑整体评估的最小误差，因此，灰色系统在学习阶段初始过程中存在数值突变的现象。

BP神经网络分别采用窗口平移多项式及小波分析的处理结果作为学习样本时，直线段区域学习及预测的总过程如图7、图8所示。

图7 直线段-2 BP神经网络基于窗口平移多项式的学习预测总过程图

图8 直线段-2 BP神经网路基于小波分析的学习预测总过程图

两种预测结果与原数据对照的标准差和相关性系数如表3所示。

表3 直线段-2 BP预测误差分析表

分析BP神经网络的学习预测总过程曲线，发现该曲线的拟合程度较灰色系统的学习预测总过程曲线更加贴切原始数据。BP神经网络在算法上属于前馈网络，在其算法学习阶段的代码中，采用了寻求最佳隐含层的for循环语句，使其算法学习结果更加贴近学习样本，因此其整体过程呈上凸型曲线，更加符合直线段-2区域的数据预期。

3.2 曲线段区域的平滑处理与预测

在MATLAB中，窗口平移多项式与小波分析对曲线段-1的平滑处理结果图如图9～图11所示。

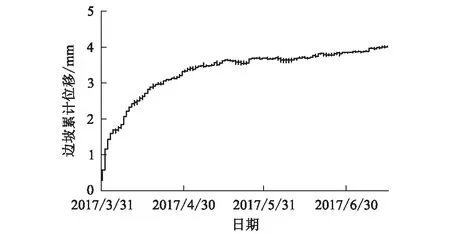
图9 曲线段-1 窗口平移多项式拟合结果图

图10 曲线段-1 小波分析拟合结果图

图11 曲线段-1原始观测位移时序图

两者平滑处理结果与原数据对照的标准差和相关性系数如表4所示。

表4 曲线段-1 处理误差分析表

分析两段曲线可知，两种方法对曲线数据的处理能力相似，效果较好，表现为标准差较小，相关性系数高。

灰色系统分别采用窗口平移多项式及小波分析的处理结果作为学习样本时，曲线段区域学习及预测的总过程如图12、图13所示。两种预测结果与原数据对照的标准差和相关性系数如表5所示。

图12 曲线段-2 灰色系统GM(1,1)基于窗口平移多项式的预测总过程图

图13 曲线段-2 灰色系统GM(1,1)基于小波分析的预测总过程图

分析灰色系统在曲线段的学习及预测过程可知，灰色系统在模拟曲线段数据时效果更加不理想，进一步论证了灰色系统在处理非指数特性数据时的不适应性。

表5 曲线段-2灰色系统GM(1,1)预测误差分析表

BP神经网络分别采用窗口平移多项式及小波分析的处理结果作为学习样本时，曲线段区域学习及预测的总过程如图14、图15所示，两种预测结果与原数据对照的标准差和相关性系数如表6所示。

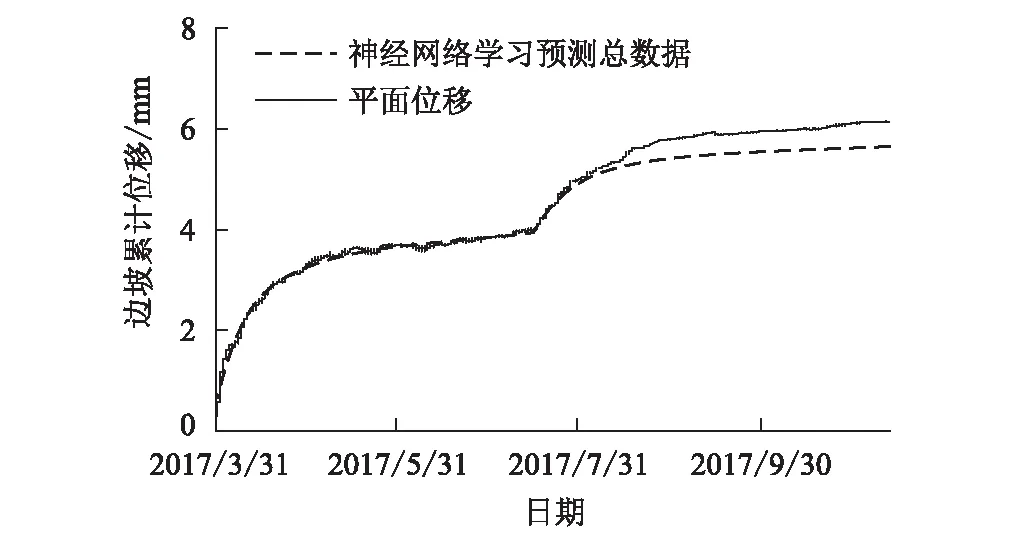
图14 曲线段-2 BP神经网络基于窗口平移多项式的预测总过程图

图15 曲线段-2 BP神经网路基于小波分析的预测总过程图

表6 曲线段-2 BP预测误差分析表

分析BP神经网络在曲线段的学习预测过程可知，在曲线段数据处理中，BP神经网络的处理效果要明显优于灰色系统GM(1,1)。当BP神经网络的学习样本为小波分析平滑结果时，其预测值更采用窗口平移多项式平滑结果要更贴近边坡实测位移。尽管视觉效果上两种预处理方法结果如出一辙，但根据各自处理结果的标准差及相关性系数可知，小波分析的预测总过程结果拟合程度更好，对于BP神经网络的学习预测能力有较强的推进作用。

4 结论

本文在排除边坡工程地质条件等现场因素的前提下，在边坡变形数据预处理及预测方法中各比选了两种常见方法，耦合成四种方法组，研究了边坡位移处于直线抬升和曲线变化不同趋势条件时，不同预处理方法对后期变形预测精确度的影响，并分别推荐了最佳数据处理方案。

(1)当边坡变形处于稳定时期时，其变形位移时序图大致呈直线趋势，窗口平移多项式对提高预测模型的精确度有明显效果，此时采用基于窗口平移多项式的BP神经网络能够获得较为精确地边坡变形预测。

(2)当边坡变形处于活跃时期时，其变形位移时序图大致呈阶跃式曲线特征，此时小波分析对提高预测模型的精确度有明显效果，此时采用基于小波分析的BP神经网络能够获得较为精确的边坡变形预测。

以上结论可为研究复杂因素影响下的边坡变形预测提供有效借鉴。