含软弱夹层边坡稳定性上限分析法研究与评价

付一鸣 王 珍 万 峰 张洪清

（1.辽宁工程技术大学矿业学院，辽宁 阜新 123000；2.本溪钢铁（集团）矿业有限责任公司歪头山铁矿，辽宁 本溪 117000；3.黄河科技学院建筑工程学院，河南 郑州 450063；4.扎赉诺尔煤业有限责任公司，内蒙古 满洲里 021410）

0 引言

软弱夹层是指在边坡岩土体内广泛存在的不连续结构面，由于其力学性质薄弱，是导致边坡发生滑坡灾害的重要因素。

软弱夹层对边坡稳定性影响已成为当下岩土工程中重要课题。现阶段，边坡工程领域常用的分析方法包括极限平衡法、极限分析法等方法［1］。上世纪20年代，学者Fellenius提出瑞典圆弧法［2］，该方法被认为是极限平衡法的开端。之后，简化Bishop法［3］、Morgenstern-Price法［4］、Sarma法［5］等极限平衡法相继提出并广泛应用。极限平衡法从力与力矩平衡角度进行稳定性求解，具有完善、成熟的理论体系。但极限平衡法弊端也是十分明显的，该方法由于不能有效考虑岩土体应力应变关系，须引入大量假设条件才可解决边坡稳定性问题，而引入的假定条件会使该方法严密性不足［6］。自上世纪中期以来，随着力学理论的快速发展，基于塑性力学中关联及非关联流动法则衍生的极限分析法成为边坡工程领域研究热点。其中上限分析法从能量与速度的角度进行边坡稳定性分析，计算过程严谨，可解决边坡岩土体破坏中的运动学问题。学者Chen［7］率先将上限分析法应用至边坡工程领域，并详细说明了上限分析法在边坡稳定性分析中的计算过程及程序实现。学者Donald［8］将对边坡破坏区域内的岩土体进行斜条分划，提出斜条分法与平动运动场相结合的上限分析法，有效扩宽了该方法的适用范围。显然，上限分析法在稳定性分析中具有一定优点，但由于计算的限制，该方法在含软弱夹层边坡稳定性分析中应用较少。

为解决该问题，本项目应用力学理论分析的方法建立含软弱夹层边坡破坏机构，基于最小二乘法拟合推导边坡岩土体外力功率及内能耗散率计算公式，并结合上限分析定理以及强度折减原理，编制含软弱夹层边坡稳定性分析循环程序，最终达到含软弱夹层边坡稳定性上限分析法求解的目标。

1 边坡稳定性分析

1.1 破坏机构的构建

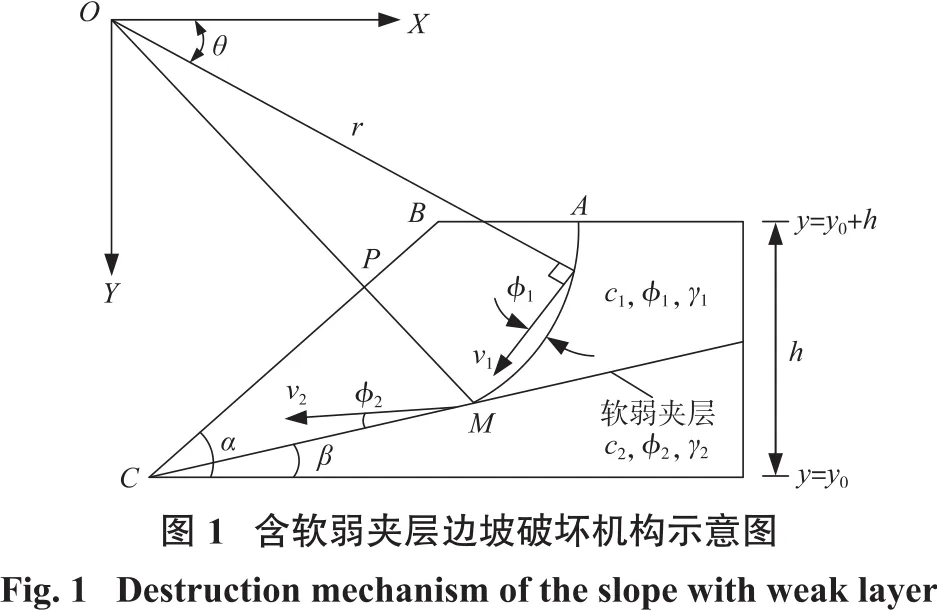
由于软弱夹层力学性质薄弱，对于含软弱夹层边坡，其潜在破坏模式为以软弱夹层为底界面的剪切—顺层破坏。由于含软弱夹层边坡破坏时部分岩土体沿弱层面滑动，因此边坡破坏机构由转动破坏机构和平动破坏机构两部分共同构成。对于含软弱夹层边坡，岩土体黏聚力为c1，内摩擦角为ϕ1，容重为γ1，软弱夹层黏聚力为c2，内摩擦角为ϕ2，容重为γ2，则该边坡破坏机构如图1所示。

图1中，边坡高度为h，坡面角为α，软弱夹层倾角为β，破坏机构由转动破坏机构（对数螺旋线AM）与平动破坏机构（软弱夹层线CM）共同构成。

1.2 计算模型的建立

计算模型的建立是进行边坡稳定性分析的重要基础，上限分析法是从能量和速度的角度进行边坡稳定性分析，因此分别建立边坡几何模型与运动学模型，并将2种模型结合进行稳定性分析。

1.2.1 几何模型的建立

图1中，r为转动破坏机构与旋转中心连线的线段距离，m；θ为转动破坏机构与旋转中心连线的线段水平向夹角，rad；则该边坡转动破坏机构方程可表示为

式中，a为方程待定参数。

以旋转中心O点为原点，分别以水平方向以及竖直方向为坐标轴的X轴、Y轴，建立直角坐标系。则根据极坐标与直角坐标的转换关系，式（1）可进一步表示为

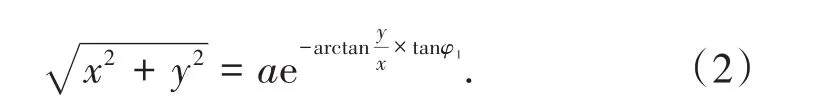
显然，式（2）是只关于x、y2个未知数的隐函数，同时该隐函数无法进行有效的显化处理。因此，本研究采用最小二乘法的方式对该隐函数进行拟合。由于边坡破坏机构为严格增函数，因此只对增区间内进行多项式拟合，令拟合结果为x=f（a，y）。

同时，在直角坐标系下，令该边坡的坡底线方程为y=y0，则该边坡的坡顶线方程为y=y0+h。边坡坡面角为α，软弱夹层倾角为β，则坡面方程f（y）以及软弱夹层方程g（y）可分别表示为

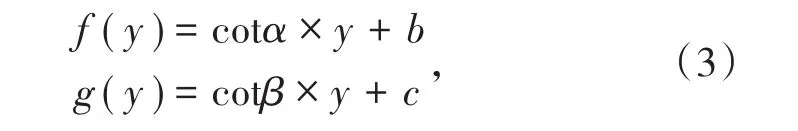
式中，b、c分别为坡面方程及软弱夹层方程中的待定参数。

图1中，对数螺旋线与软弱夹层相交点为M，令M点坐标为（xm，ym），则平面直角坐标系下直线OM方程可表示为

直线OM将边坡破坏区域划分为两部分，直线OM上部（曲变形ABPM）为转动破坏区域，该区域应用几何公式可表示为

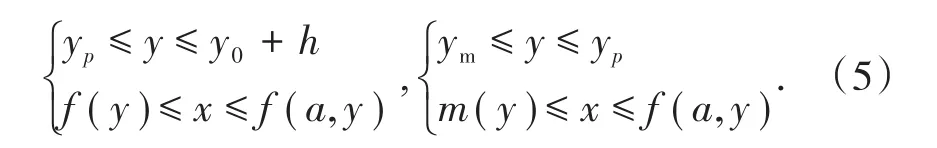
直线OM下部（三角形CPM）为平动破坏区域，该区域应用几何公式可表示为

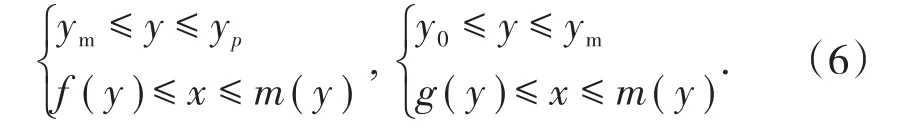
式（5）和式（6）中，yp为P点的纵坐标，可通过边坡坡面方程f（y）与直线OM方程m（y）结合求得。

1.2.2 运动学模型的建立

曲变形ABPM为转动破坏区域，该区域内滑体以固定角速度ω绕旋转中心O转动运动，则该区域内滑体速度可表示为

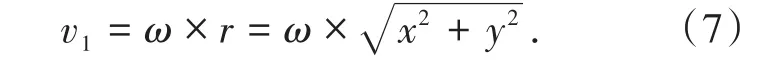
三角形CPM为平动破坏区域，该区域内滑体以固定线速度平动运动。边坡破坏区域内形成多块体的破坏模式，相邻的块体之间应满足速度相容关系［9］。M点速度相容关系如图2所示。

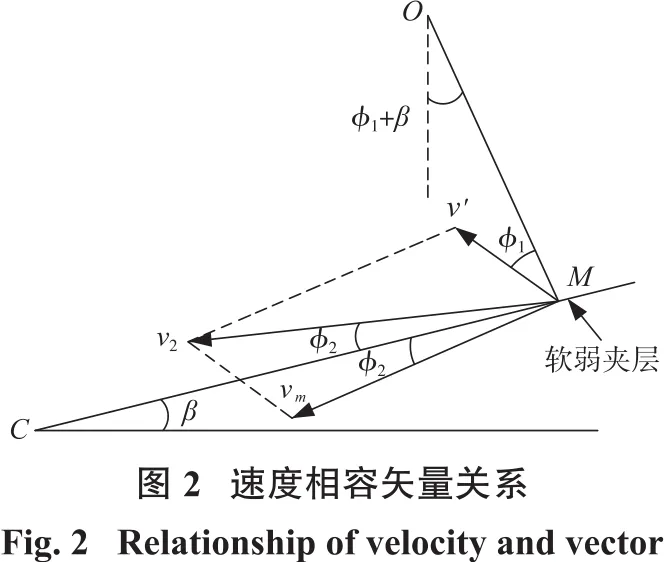
图2中vm为转动破坏区域滑体速度，v2为平动破坏区域滑体速度，v'为OM上块体相对速度。显然，线段OM、软弱夹层CM均为速度间断面。根据图2中的速度相容关系图，可确定平动破坏区域滑体速度v2可表示为

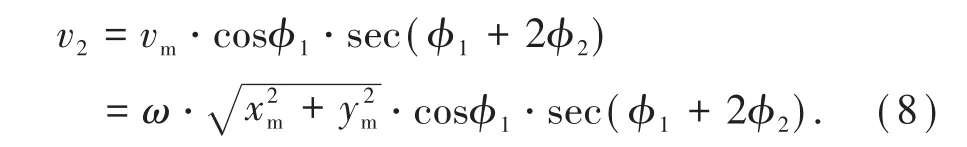
1.3 上限分析计算

上限分析法是从能量与速度的角度进行边坡稳定性分析，其理论基础为当边坡坡体内的岩土体处于极限平衡状态时，外力功率应该等于其内部能量耗散率。因此，下文对含软弱夹层边坡破坏区域岩土体外力功率以及内能耗散率分别进行计算。

1.3.1 外力功率计算方法

自然状态下，含软弱夹层边坡坡体内外力功率由重力提供，因此：

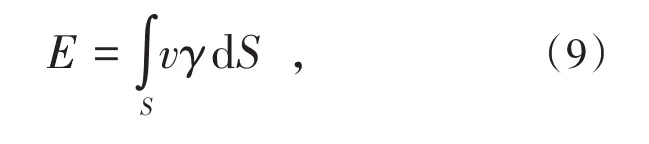
式中，E为含软弱夹层边坡坡体内的外力功率，kW；dS为任意取出的面积微元，m2；v为该微元对应的重力方向分速度，m/s。

由于转动破坏区域与平动破坏区域速度求解方式不同，因此分别对转动破坏区域与平动破坏区域外力功率进行求解。

对于转动破坏区域，面积微元在重力方向上分速度为v1cosθ，根据式（7）重力方向分速度可简化为ωx，则转动破坏区域外力功率E1可表示为

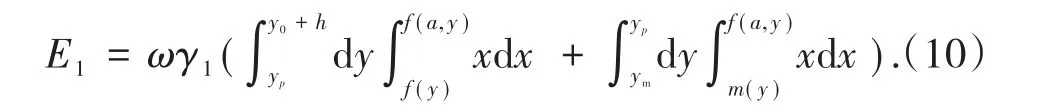
对于平动破坏区域，面积微元在重力方向上分速度为v2sin(β−ϕ2)，则平动破坏区域外力功率E2可表示为

该边坡破坏区域外力功率可通过转动破坏区域外力功率E1与平动破坏区域外力功率E2二者相加求得，即E=E1+E2。

1.3.2 内能耗散率计算方法

传统的力学理论认为，摩擦能耗与剪胀能耗恰好可以抵消，因此含软弱夹层边坡破坏区域内能耗散全部由黏聚力提供，且全部集中于速度间断面上。图1中边坡速度间断面由对数螺旋线AM、软弱夹层CM以及线段OM三部分构成，因此，分别对上述三部分内能耗散率求解。

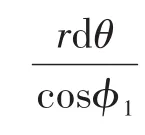
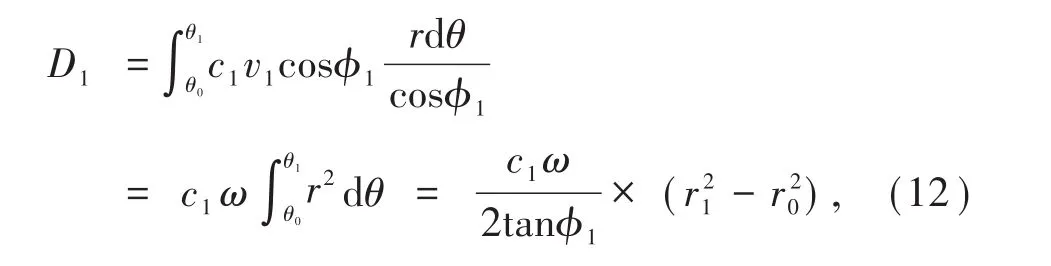
式中，θ0为线段OA的水平方向夹角，rad；r0为线段OA的长度，m；θ1为线段OM的水平方向夹角，rad；r1为线段OM的长度，m。

根据2点之间的距离计算公式，对图1中AM上的内能耗散率可表示为

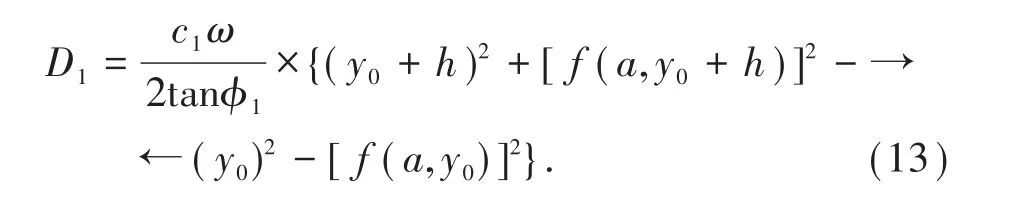
对于软弱夹层CM，平动破坏区域滑体在软弱夹层方向上分速度为v2cosϕ2，因此图1中软弱夹层CM上的内能耗散率D2可表示为

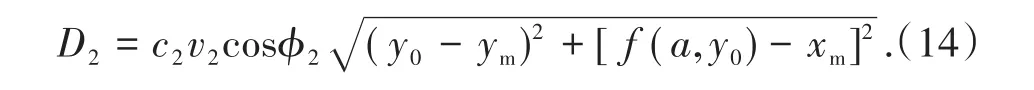
对于速度间断面OM，转动破坏区域滑体在OM方向上分速度为0，平动破坏区域滑体在OM方向上分速度为v2sin2ϕ2。因此OM上内能耗散率D3可表示为

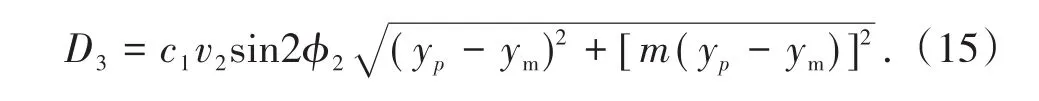
则该边坡内能耗散率可通过三部分内能耗散率相加求得，即D=D1+D2+D3。

1.3.3 强度折减运算

上文中给出了含软弱夹层边坡功率的计算方法，为使含软弱夹层边坡逐渐过渡至极限平衡状态，同时考虑到利于计算机编程的需求，本研究结合强度折减法进行稳定性分析，其公式为

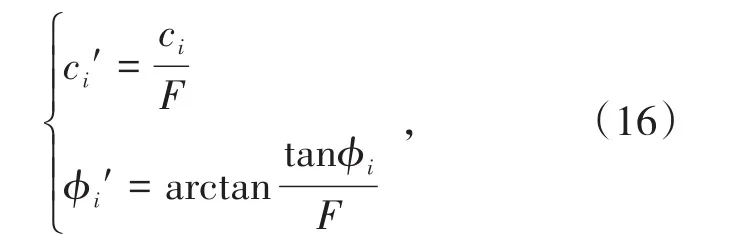
式中，F为强度折减系数。显然，通过人工计算的手段将含软弱夹层边坡折减到极限平衡状态十分复杂，本项目借助计算机编程技术实现对于含软弱夹层边坡稳定性分析的强度折减。

1.3.4 计算机循环编程

强度折减规律表明，当岩土体强度折减系数等于边坡稳定系数时，含软弱夹层边坡破坏区域外力功率与内能耗散率二者恰好相等。同时，强度折减系数与二者比值呈现严格相关性。基于上述特性，本项目构建函数ε=（D/E-1）min，显然函数ε在［0，+∞）上只有一个零点，可采用二分法进行稳定系数求解。同时为使程序可有效终止，本项目将满足∣ε∣≤0.001近似为计算零点，并作为边坡稳定性分析程序的终止条件。

经过边坡稳定性分析二分法计算流程可输出满足∣ε∣≤0.001的折减系数。同时当D/E-1取得最小值时，根据各参数值可绘制边坡滑裂面。该折减系数及滑裂面形态即为边坡稳定系数及最危险滑面，因此可最终实现含软弱夹层边坡稳定性分析的目标。

2 算例分析

某露天矿山形成的边坡坡高为120 m，坡面角α=25°，岩性为炭质泥岩，粘聚力c1=150 kPa，内摩擦角ϕ1=30°，容重γ1=20 kN/m3。边坡岩土体内发育有通过边坡坡趾的软弱夹层，倾角β=5°，黏聚力c2=30 kPa，内摩擦角ϕ2=10°，容重γ2=12 kN/m3，边坡形态及破坏机构如图3所示。

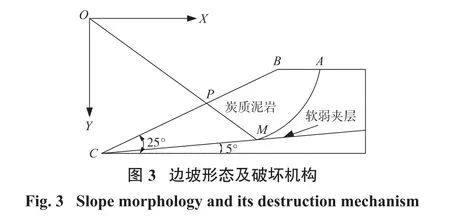
2.1 边坡稳定性计算

根据计算流程，选取初始值a1=0，b1=3，则在第一次的循环程序中，中值F1=1.5。经过强度折减后c1'=100 kPa，ϕ1'=21.05°，c2=20 kPa，ϕ2'=6.7°，则对数螺旋线AM的表达式为

函数增区间为y∈（-0.417a，-1.831a），对区间内函数表达式进行多项式拟合，拟合结果为

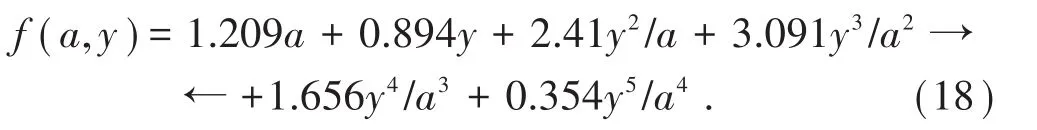
同时，在平面直角坐标系下，边坡坡底线方程为y=y0，坡顶线方程为y=y0+120，边坡坡面方程为f（y）=2.145y+b，软弱夹层方程为g（y）=11.43y+c，直线OM方程为m（y）=xm×y/ym。则含软弱夹层边坡功率计算公式可分别表示为

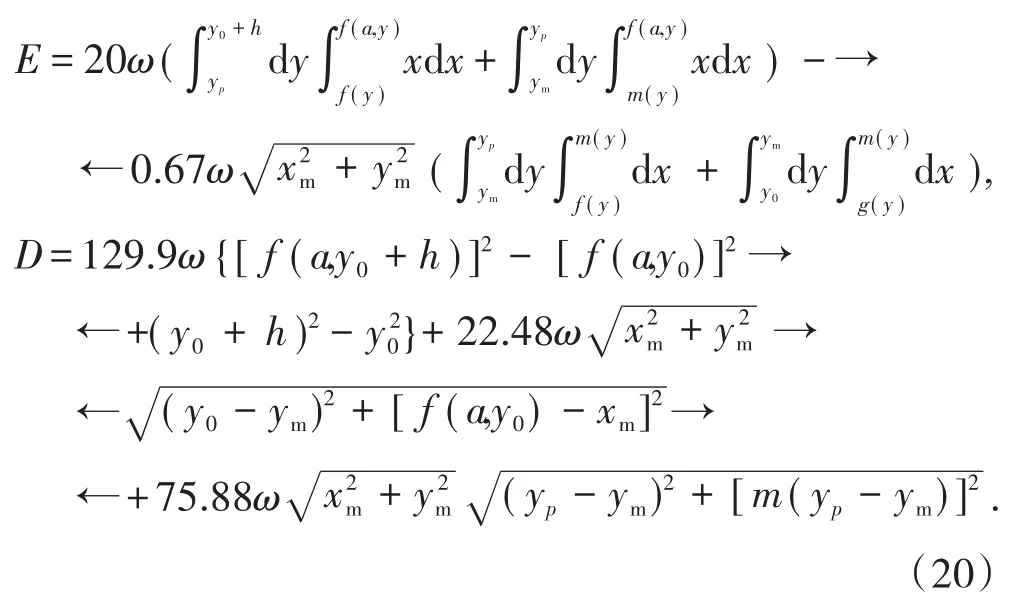
为确定内能耗散率与外力功率的比值，应针对边坡工程特性给出相应的约束条件。根据边坡工程实践，各参数应满足以下方面约束条件：①边坡坡面与软弱夹层相交于边坡坡趾C点，则约束条件为f（y0）=g（y0）；②对数螺旋线与软弱夹层相交于点M，则约束条件为xm=g（ym）=f（a，ym）；③边坡坡面与直线OM相交于点P，则约束条件为xp=f（yp）=f（a，yp）；④对数螺旋线位于第四象限增区间，则约束条件为 -0.417a≤ym≤-1.831a，-0.417a≤y0+120≤-1.831a；⑤边坡破坏机构位于边坡坡面内部，则约束条件为f（a，y）-f（y）≥0，y∈（ym，y0）。

根据内能耗散率与外力功率计算公式以及上述约束条件，可求得D/E-1的最小值ε。第一次循环中，强度折减系数F=1.5，求得ε<-0.001，不满足∣ε∣≤0.001的程序终止要求，因此进入下一次循环。反复执行运算可最终输出满足∣ε∣≤0.001的折减系数，循环计算结果如表1所示。

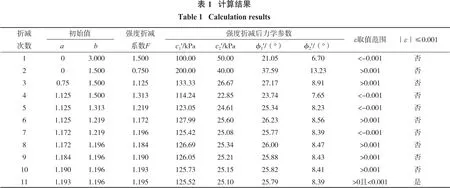
表1表明：经过11次循环，输出的计算结果满足∣ε∣≤0.001要求，此时折减系数为1.195，则该边坡稳定系数Fs=1.195。同时，根据各参数值可绘制含软弱夹层边坡最危险滑面，上限分析法稳定性分析结果见后文图4。

2.2 计算结果评价

根据前文中分析可知，上限分析法和极限平衡法分析角度完全不同，但对于同一边坡，其稳定性分析结果应是一致的。考虑到极限平衡法中简化Janbu法对于含软弱夹层边坡具有良好适用性，因此选取简化Janbu法对上限分析法计算结果进行准确性评价。简化Janbu法稳定性分析结果如图4所示。

从稳定系数的角度分析，两方法计算偏差小于5%，表明两方法都具备较高的准确性。简化Janbu法虽然对于含软弱夹层边坡稳定性具有良好适用性，但由于其求解结果并非严格的上限解或下限解，计算误差无法估算。而上限分析法对于含软弱夹层边坡稳定系数的计算结果为严格上限解，计算误差可通过工程经验进行消除［10］。

从最危险滑面形态的角度分析，两方法最危险滑面在软弱夹层处交点位置近似相同，表明两方法求得的最危险滑面平动破坏机构形态近似相同。相比于简化Janbu法，上限分析法最危险滑面起始点更靠近于边坡后部，表明两方法最危险滑面转动破坏机构形态存在一定差异。上限分析法求得最危险滑面转动破坏机构形态为对数螺旋线，而剩余推力法求得最危险滑面转动破坏机构形态为圆弧线，根据Mohr-Coulomb屈服准则，上限分析法求得的最危险滑面形态可有效满足岩土体材料的速度分离要求。因此从最危险滑面形态的角度分析，上限分析法计算结果具有更强的工程实践意义。

3 结 论

（1）应用力学理论分析构建了满足关联流动法则及速度分离要求的含软弱夹层边坡破坏机构。

（2）建立了含软弱夹层边坡破坏机构几何模型和运动学模型，并基于最小二乘拟合的方式推导了含软弱夹层边坡破坏机构外力功率及内能耗散率计算公式。

（3）综合应用上限分析定理和强度折减原理，编制了含软弱夹层边坡稳定性上限分析法计算机循环程序，并通过工程算例对上限分析法计算结果进行了准确性评价，充分验证了该方法计算结果的可靠性。