基于机器学习的跨患者癫痫自动检测算法
杨舒涵, 李 博, 周丰丰
(1. 吉林大学 计算机科学与技术学院, 长春 130012;2. 吉林大学 符号计算与知识工程教育部重点实验室, 长春 130012;3. 吉林大学 软件学院, 长春 130012)
癫痫是一种神经系统的疾病[1], 严重危害患者的生命安全. 癫痫检测可帮助医生更好地了解患者的发病信息, 并根据检测结果结合其他检测工具, 实现病灶定位. 传统检测方法是通过询问患者家属关于患者的以往发病史, 并观察患者的脑电数据, 得出结论. 脑电数据, 即脑电图(electroencephalo-graphy, EEG), 是一组随时间变化连续的一维数据, 可记录大脑活动时的电信号. 癫痫发作时, 通常会伴有大脑神经元的异常放电, 因此脑电数据对癫痫的检测有很大帮助. 癫痫检测被视为一个二分类问题, 分为发作期和发作间期, 发作间期指两次发作期之间的时刻. 目前对癫痫自动检测的研究多集中于专人专治, 即为每个患者建立自身的检测模型. Vidyaratne等[2]先使用快速小波分解和分形维数方法对脑电数据进行特征提取, 再使用相关支持向量机模型进行分类, 实现了模型与患者相关的癫痫检测. 该方法分类结果较好, 但是也存在以下问题: 首先, 模型的建立需要患者的以往发病记录, 而当患者无发病记录时, 即无法为该患者进行检测; 其次, 该模型不具有泛化性, 即一个患者的模型无法适用于其他患者.
针对上述问题, 本文提出一种使用机器学习的跨患者癫痫自动检测算法. 该算法首先使用滤波器对原始脑电数据进行固定频率范围的数据过滤, 达到去除噪声的目的; 然后从时域角度和非线性角度对滤波后的数据进行特征提取; 再使用递归特征消除(recursive feature elimination, RFE)和序列后向选择(sequential backward selection, SBS)算法对提取到的特征做进一步筛选, 被选择特征作为分类模型的输入数据; 最后用XGBoost(eXtreme gradient Boosting)模型分类, 实现癫痫的自动检测. 本文检测算法在特征提取后增加了基于XGBoost模型的特征选择算法, 能选择出更具有代表性和泛化性的特征, 并使用XGBoost模型进行分类. 实验结果表明, 该方法不仅减少了特征数量, 简化了模型的复杂度, 且提升了模型的分类性能.
1 跨患者的癫痫自动检测模型
本文癫痫自动检测算法基于采集到的脑电数据, 通过一系列机器学习算法得到最具代表性的特征矩阵, 然后输入到分类模型中, 得到最终的分类结果. 实验流程如图1所示.

图1 癫痫自动检测实验流程Fig.1 Experimental process of automatic epileptic seizure detection
1.1 数据预处理
常用的脑电数据是通过将电极放置在患者头皮上采集得到的, 这种采集方式对人体无伤害, 成本较低, 患者易接受, 但因为是外置电极, 所以很可能受外界干扰, 导致数据中掺杂一些噪声, 影响最后的分类结果. 滤波算法是一种常见的去除脑电信号中噪声的方法, 本文使用带通滤波器, 其可使一个特定频段的数据通过滤波器, 而抑制或削弱其他频段的数据. 常用于癫痫病诊断的频段为0.01~32 Hz[2], 在该范围内的频段又分为4种不同的脑波, 分别为δ波(1~3 Hz)、θ波(4~7 Hz)、α波(8~13 Hz)和β波(14~30 Hz)[3]. 因此, 本文分别使用四阶Butterworth滤波器、 Chebyshev滤波器、 Bézier滤波器和椭圆滤波器对原始的脑电数据进行0.01~32 Hz的滤波, 并研究不同类型脑电波的特征.
1.2 特征提取
原始的脑电信号数据量较大, 数据不具有代表性, 使用特征提取方法可提炼出更有意义的数据建立模型. 本文主要从时域角度和非线性角度对脑电数据进行特征提取.
设T为脑电数据. 对于时域特征提取, 本文从一段脑电数据T中主要提取了21种特征, 其中前11种包括数据的最大值(maxT)、 最小值(minT)、 平均值(meanT)、 标准差(stdT)、 方差(varT)、 总体变化量(totalT)、 偏斜度(Skewness)、 峰度(Kurtosis)、 平均能量比(APR)、 峰值(Peak)和均峰比(PAR). 定义一段时长的脑电数据T=(T1,T2,…,Tn), 其中n为数据点个数. 则总体变化量计算公式为

(1)
偏斜度计算公式为

(2)
其中E表示对括号中值求期望; 峰度计算公式为

(3)
平均能量比计算公式为

(4)
峰值计算公式为
Peak=max{|maxT|,|minT|};
(5)
均峰比计算公式为
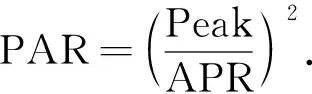
(6)
后10种特征是根据脑电数据波动情况得到的一种百分数, 计算步骤如下:
1) 创建数组L=(L1,L2,…,Lk), 用于保存一段时长脑电信号T中相邻波峰(相邻数据点的值均小于当前数据点的值)和波谷(相邻数据点的值均大于当前数据点的值)差值的绝对值.
2) 定义L_min=min{L},L_max=max{L}, winNum=10, feet=(L_max-L_min)/winNum, 其中:L_min为L中的最小值, 作为直方图横轴的左侧起始点;L_max为L中的最大值, 作为直方图横轴的右侧终止点; feet作为直方图的组距宽度. 即直方图的横轴被分为10组, 每组取值分别为[L_min,L_min+feet),(L_min+feet,L_min+2feet),…,(L_min+9feet,L_max].
3) 统计L中数据落在直方图中每个组内的个数, 并除以数组L的长度k进行归一化, 结果定义为Bin1,Bin2,…,Bin10, 该结果即为后10个时域特征.
对于非线性特征提取, 本文提取了8种特征, 分别为小波熵(WaveletEn)[4-5]、 信息熵(SampEn)[6]、 排列熵(PeEn)[7]、 去趋势波动分析方法(DFA)[8]得到的实验结果、 分形维数值(PFD)、 RS法计算得到的Hurst指数以及使用Hjorth参数计算得到的移动性值(mobility, HM)和复杂性值(complexity, HC)[9]. 实验采用的所有特征提取方法已整理为python代码上传至https://github.com/yangsh827/Seizure_FE. 本文特征提取阶段获得的特征列于表1.

表1 根据脑电数据提取的特征Table 1 Features extracted by EEG data
1.3 特征选择
本文结合计算机领域与生物医学领域的相关知识, 使用机器学习算法实现跨患者的癫痫自动检测. 生物医学领域的数据具有样本少、 特征多的特点, 当输入分类模型的特征接近或大于样本数时, 会增加分类模型的复杂度, 模型很可能出现过拟合的情形, 使其不具有泛化性, 同时还会增加模型的训练时间. 因此, 需要对特征矩阵进行特征选择. 目前在机器学习中, 特征选择通常分为3种类型: 过滤式、 包装式和嵌入式, 如图2所示.

图2 特征选择的分类Fig.2 Classification of feature selection
本文主要使用包装式中的两种特征选择算法, 一种是递归特征消除法RFE, 另一种是基于贪心算法的SBS. 首先将特征提取后的特征矩阵进行RFE特征选择. RFE是一种常用的特征选择算法, 其主要思想是先在原始的特征矩阵中递归地删除特征, 然后用剩余的特征构建模型. 通过模型的评价指标判断哪些特征(或特征组合)对预测结果贡献较小, 从而对其进行剔除. 该算法的时间复杂度为O(n), 算法步骤如下:
1) 归一化处理特征提取后的特征矩阵, 将其结果作为RFE算法的输入数据;
2) 选择一种可得到各特征权重的模型作为基分类器, 设每轮训练减少的特征数为n, 最终要保留的特征数为k, 选择模型的评价指标;
3) 对输入数据集进行训练, 得到各特征的权重, 并用五折交叉验证得到该模型各评价指标值;
4) 将特征的权重从大到小排列, 从数据集中移除n个拥有最小绝对值权重的特征, 得到下一轮输入的数据集;
5) 重复步骤3),4), 当剩余特征数为k时, 算法停止.
实验中, 设参数n=1,k=1, 即每次去除一个特征, 在特征数减少到1时RFE算法停止. 通过步骤3), 可得每轮交叉验证的结果, 选择具有最好性能模型对应的特征数, 作为本文实验RFE算法最终选择出的特征数.
经过RFE特征选择后, 使用SBS算法对特征进行进一步筛选. SBS算法是一种启发式搜索算法, 使用贪心算法的思想. 该方法选择一个模型作为基分类器, 每次从特征矩阵中移除一个特征, 使特征矩阵在移除该特征后得到的评价指标相对于移除其他特征是最优的. SBS算法由于在每次移除特征时, 都要对剩余的所有特征模型进行训练, 因此该算法的时间复杂度为O(n2), 故将其作为RFE特征选择后的进一步筛选.
1.4 分类模型
本文使用的分类器以及在RFE和SBS算法中使用的基分类器均为XGBoost模型, 其为一种集成的机器学习模型, 该模型在各项算法竞赛中均表现良好, 因此本文使用XGBoost作为分类模型.
2 数据集与评价指标
2.1 数据集
实验采用CHB-MIT头皮脑电信号公开数据集. 该数据集采集于美国波士顿一家儿童医院, 共记录了23名癫痫患者的脑电数据, 采样频率为256 Hz, 共包含157次癫痫发作. 数据采集时, 电极在患者头皮的放置位置遵循国际标准10-20系统. 该数据集中大部分样本均包含22个通道(FP1-F7,F7-T7,T7-P7,P7-O1,FP1-F3,F3-C3,C3-P3,P3-O1,FZ-CZ,CZ-PZ,FP2-F4,F4-C4,C4-P4,P4-O2,FP2-F8,F8-T8,T8-P8,P8-O2,P7-T7,T7-FT9,FT9-FT10,FT10-T8)的数据, 因此本文仅使用包含上述22个通道的样本. 同时, 因为chb12患者的发作间期持续时间较短(平均415 s), chb16患者的发作期持续时间较短(平均8.6 s), 因此未采用这两位患者的数据.
实现癫痫的自动检测, 使用的检测数据时长不应过长, 因此, 本文将检测时长设为6 s, 即将发作期的数据以6 s为一个窗口进行无重叠滑动, 不足6 s的数据将被舍弃, 得到正样本集合. 发作间期的数据也以6 s为一个窗口进行滑动, 得到负样本集合. 因为发作间期时长远大于发作期时长, 为避免由正负样本数据量不平衡而导致模型偏向某类样本, 因此本文实验在负样本中进行随机采样, 最终使正负样本数据量相同, 得到正负样本各1 260个.
2.2 评价指标
使用准确率(accuracy, Acc)、 敏感性值(sensitivity, Sn)和特异性值(specificity, Sp)测试算法的性能. 准确率Acc定义为分类正确的样本占所有样本的比例, 计算公式为
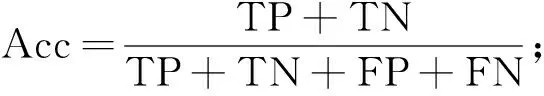
(7)
敏感性值Sn定义为分类正确的正样本占所有正样本的比例, 即正确判断为患病的比例, 计算公式为

(8)
特异性值Sp定义为分类正确的负样本占所有负样本的比例, 即正确判断为非患病的比例, 计算公式为
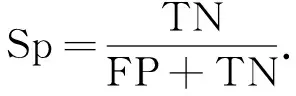
(9)
3 实验结果与分析
3.1 实验环境
本文用Python 3.6.4作为开发环境, 所用sklearn数据库版本为0.19.1, numpy数据库版本为1.16.3, pandas数据库版本为0.22.0, scipy数据库版本为1.0.0, XGBoost版本为0.71. 实验环境需要安装nolds数据库(https://pypi.org/project/nolds/)和PyWavelet数据库(https://pywavelets.readthedocs.io/en/latest/install.html). 实验中各种算法的参数设置均使用函数默认参数.
3.2 结果分析
先分别使用Butterworth滤波器、 Chebysher滤波器、 Bézier滤波器和椭圆滤波器对原始脑电数据进行0.01~32 Hz的带通滤波, 然后对滤波后的数据特征提取, 经过五折交叉验证, 所得实验结果列于表2. 由表2可见, 先用Butterworth滤波器对原始脑电数据进行滤波, 然后再进行特征提取, 得到的准确率Acc、 敏感性值Sn和特异性值Sp均高于其他3种滤波器, 说明Butterworth滤波器更适合本文癫痫检测方法.

表2 4种滤波器的分类结果Table 2 Classification results of four filters
下面用Butterworth滤波器进一步分析不同频率范围的4种脑波(δ波、θ波、α波和β波)与癫痫检测的关系. 用Butterworth滤波器先分别对脑电数据进行4种脑波对应频率范围的带通滤波, 然后对滤波后的脑电数据特征提取, 经过五折交叉验证, 所得实验结果列于表3. 由表3可见, 对于综合准确率Acc、 敏感性值Sn和特异性值Sp,β波(14~30 Hz)的分类结果比0.01~32 Hz频率范围和其他脑波的分类结果更优. 而β波是一种人在紧张情形下释放的脑波, 实验结果表明, 14~30 Hz频率范围的β波脑电数据更适合于本文检测方法.

表3 在4种脑波上的癫痫分类结果Table 3 Classification results of epileptic seizure of four brain waves
用Butterworth滤波器对原始脑电数据进行β波(14~30 Hz)滤波去噪, 再进行特征提取, 共得到638个特征. 对这638个特征进行RFE特征选择, 再对选择后的特征矩阵使用SBS算法做进一步筛选, 经过五折交叉验证, 每种特征选择算法所得分类结果列于表4. 表4中特征数(features numbers, FNums)表示使用两种特征选择算法得到的最好分类准确率对应的特征数. 由表4可见: RFE算法将原始特征数由638个减少到66个, 分类准确率提升了2.5%; SBS算法将RFE选择后的特征数由66个减少到44个, 分类准确率提升了1.63%. 表明机器学习中的特征选择算法不仅提高了分类性能, 同时减少了特征数量. 因此, 针对经过特征提取的数据, 用本文的特征选择算法可极大提高分类性能. 本文算法、 神经网络算法[10]和随机森林算法[11]的敏感性分别为0.854 8,0.850 0,0.808 7, 表明本文算法在敏感性值上优于另外两种对比算法, 说明本文算法效果更佳.

表4 特征选择算法RFE和SBS的分类结果Table 4 Classification results of feature selection algorithms of RFE and SBS
综上所述, 本文提出了一种基于机器学习算法的跨患者癫痫自动检测算法. 首先对原始脑电数据用滤波器去除噪声, 从时域和非线性角度对去除噪声后的脑电数据进行特征提取, 并在4种滤波器和5种频率范围的脑波中找出了更适合跨患者癫痫检测的Butterworth滤波器和β脑波; 然后用基于XGBoost基学习器的特征选择算法RFE和SBS对特征矩阵实现进一步的特征筛选; 最后在638个特征中保留了44个特征. 实验结果表明, 本文使用机器学习算法, 在更少特征的情形下实现了更高的分类性能, 分类准确率Acc为0.877 4, 敏感性值Sn为0.854 8, 特异性值为0.9. 该结果在准确率上比特征选择前提升了4.13%, 且在跨患者癫痫检测模型中表现出更优的性能, 表明本文算法检测性能更高、 效果更好.

