混合基础隔震耗能结构基于Clough-Penzien谱的地震动响应的简明解析解

林桂武, 葛新广, 李 暾

(广西科技大学 土木建筑学院， 广西 柳州 545006)

基础隔震是一种业已成功应用于实际工程的有效被动控制措施[1-5]，其是利用隔震层的抗侧刚度相对其上部结构刚度小的特点，起到减弱地震能量向结构物传递的作用，从而降低了结构层的地震动产生的变形和内力。然而，由于隔震层的抗侧刚度小，地震时上部结构部分的刚性侧移较大，会产生不良后果：可能会与邻近建筑发生碰撞，或导致整体倾覆，或导致隔震层破坏[6-8]。因此，对隔震层侧移进行限位十分必要。韩淼等[8]利用SAP2000软件研究了弹簧软限位在近断层地震下的层间隔震结构的响应分析。程选生等[9]利用振动台试验验证了滑移隔震-限位滑移装置对储液结构及液体晃动波高具有良好的减振效果。刘臣等[10]研发了橡胶与铅芯组合而成的限位装置，能有效降低隔震结构侧移动。以上分析均以试验或软件分析为主，仅考虑的是确定性荷载。黏弹性阻尼器利用一类既能储能也能耗能的高分子材料制作的阻尼器，具有安拆方便、耗能效果好等优点，已被广泛应用抗风减振中[11-13]。Pant等[14]利用全模型试验研究了黏弹性阻尼器对于高层建筑的抗风减振效果较好。李创第等[15]利用传递矩阵法获得了一般线性黏弹性阻尼器地震动响应非正交解析解。吴福健等[16]研究了位移放大型黏弹性阻尼器对于结构地震动的影响，研究表明该类型阻尼器能有效降低结构地震动响应。由于黏弹性阻尼器是位移-速度型阻尼器，在位移和速度较大时才能发挥其减振作用，为此，隔震层设置抗侧黏弹性阻尼器，可为隔震层提供适当的侧向变形，同时充分利用黏弹性阻尼器在侧移变化率(速度)大则耗能大的特点,从而产生复合的减振效果，称之为混合基础隔振结构。Providakis[17]研究了侧向黏性阻尼器同时抑制刚性侧移及层间位移。

1947年Housner提出随机白噪声地震动激励，经过70年多年的发展，工程界已就地震动看做结构的随机外激励达成共识，提出了多种随机激励模型，如Kanai-Tajimi谱[18-19]、Clough-Penzien谱[20]、欧进萍谱[21]、李春祥谱[22]等，其中Kanai-Tajimi谱首次利用滤波方程将复杂的地震动表述为基于场地振动特征值的白噪声激励，而其他随机地震动模型均是对Kanai-Tajimi的改进，使对地震动的表述更为准确。Clough-Penzien谱利用滤波方程组改善了Kanai-Tajimi过分夸大低频的地震动能量的作用，得到了广泛应用。李创第等[23]利用复模态方法研究了多层基础隔震结构基于Clough-Penzien谱的地震动响应分析，但所给结构响应的方差表达式比较复杂，且未给出谱矩的分析，无法应用于动力可靠度分析。李春祥等[24]利用传递函数法分别研究了MTMD结构基于Kanai-Tajimi和Clough-Penzien谱的地震动响应分析，所得响应表达式仅为功率谱，且表达式复杂，而在分析结构响应方差时只能数值解，计算效率差。

针对目前分析基础隔震结构+侧向黏弹性阻尼器组成的耗能体系的随机地震动响应表达式复杂的问题进行了研究。首先建立混合耗能结构的地震动方程，并利用C-P谱的滤波方程，将混合基础隔震耗能结构基复杂的地震动转化为基于白噪声激励下的地震动；其次运用复模态方法解耦运动体系，并获得混合隔震结构随机地震动响应(结构层侧移、层间变形及其变化率)统一的杜哈梅积分表达式；利用白噪声激励协方差的性质，获得耗能体系响应协方差的简明表达式；然后基于平稳激励的Wiener-Khinchin定律，获得响应功率谱的简明解析解并基于谱矩的定义，获得混合耗能结构地震动响应的0-2阶谱矩的简明解析解；最后研究了基于首超破坏准则的混合基础隔震耗能结构的动力可靠度。

1 混合基础隔震耗能结构的地震动方程

在基础隔震层设置抗侧作用的黏弹性阻尼器组成混合基础隔震耗能结构，如图1所示。

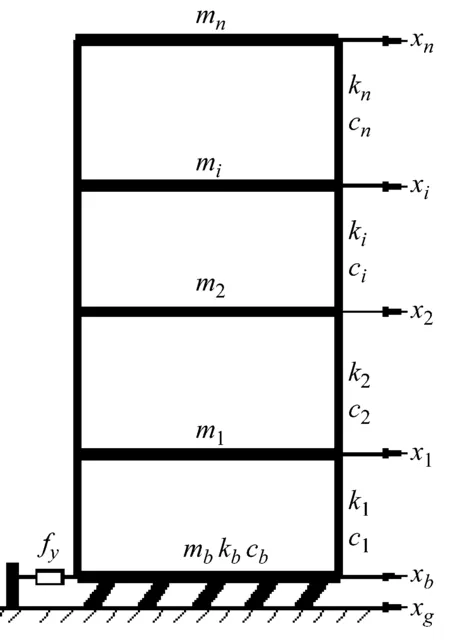
图1 计算简图

在地震动作用下运动方程

(1)

(2)

式中：λ，cV为黏弹性阻尼器的松弛时间和阻尼系数。M、C、K的具体表达式如下

地面地震动采用Clough-Penzien谱随机激励模型，其滤波方程组表示

(3a)

(3b)

(4)

式中，δ(τ)为Dirac函数。

传统方法主要是采用与式(3)等价的功率谱密度函数[25]

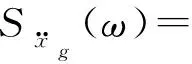
(5)

由式(5)可知，该表达式复杂，且在分析结构地震动响应的谱矩和方差时需对功率谱进行积分，只能数值积分，故存在计算效率和精度的问题。为此本文提出利用C-P谱的滤波方程与混合基础隔震耗能结构的地震动方程联合求解的方法，获得结构系列地震动响应简明解析解。

联立式(1)～(3)，用矩阵形式表示为

(6)

式中：

(7)

式中：o为元素等于0的1×(n+1)向量；o1为元素等于0的1×(n+5)向量；o2为元素等于0的(n+1)阶方阵；E为(n+1)阶单位对角阵。

由式(6)可知，基于C-P谱激励的混合隔震结构地震动响应化为白噪声激励下的响应分析，可利用白噪声激励的简明特点获得地震动响应的简明解析解。为获得结构响应的简明解，必须采用复模态方法对式(6)进行解耦。

2 混合基础隔震结构地震动响应的解析解

2.1 复模态解耦

由复模态法理论[26]可知，式(6)存在左、右特性向量矩阵U，V和特征值矩阵P，满足关系式

(8)

式中，特征值矩阵P为对角阵，其元素的实部为负实数。

引入复模态变量

y=UZ

(9)

式中：Z为广义变量。

把式(9)代入式(6)并利用复模态理论，式(6)可改写为

(10)

式中：γ为模态强度系数向量，其表达式

(11)

由于P为对角阵，则式(11)的分量表达式

(12)

式中：zj、ηj、pj分别为Z、η、P的分量。

式(12)的时域解为

(13)

2.2 地震动系列响应的统一表达式

结构层相对于地面的位移和层间地震动变形是工程结构抗震设计的关键参数；结构层相对于地面的速度方差和层间地震动位移变化率方差是结构抗震动力可靠度分析的基础。为此，本文研究了上述地震动系列响应的分析。

(14a)

(14b)

式中：μi为右特征向量矩阵U的第i行向量；结构响应的模态强度系数λj,i

λj,i=uj,iηi

(15)

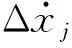
(16a)

(16b)

式中：

(17)

(18)

至此，混合基础隔震耗能结构各层位移，层间变形及其变化率的时域解可统一表示为

(19)

式中：Xl(t)表示设计变量l；κl,i表示设计变量对应的模态强度系数；Xl,i(t)为分量形式

(20)

3 响应的方差及功率谱的解析解

由式(20)，结构响应Xl的协方差为

CXl(τ)=E[Xl(t)Xl(t+τ)]=

(21)

由式(20)，结构响应分量的协方差为

(22)

把式(4)代入式(22)

(23)

利用Dirac的函数性质，式(23)简化为

E[Xl,k(t)Xl,i(t+τ)]=

(24)

对式(24)积分

(25)

由式(21)及(25)，混合基础隔震耗能结构基于C-P谱的地震动响应为

(26)

式中：

(27)

由式(26)可知，混合基础隔震耗能结构基于C-P随机激励的地震动响应的协方差可用耗能结构的振动复特征值指数的线性组合表示，表达式简洁明了，且为各模态的CQC组合。由随机振动理论可知，当τ=0时，混合基础隔震耗能结构的协方差即为其响应的方差

(28)

根据式(14)～(16)、(28)可获得混合基础隔震耗能结构地震动响应及其变化率的方差。

由随机振动理论，结构动力响应的单边功率谱与协方差存在Wiener-Khinchin关系

(29)

式中：SXl(ω)为结构响应Xl的功率谱。

把式(26)代入式(29)并积分

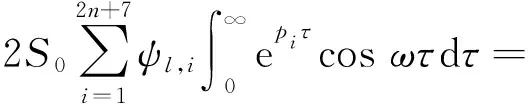
(30)

从式(30)可知，混合基础隔震耗能结构的功率谱表示成系统振动复特征值pi的频域变量ω平方和的倒数的线性组合，为后文获得简明的地震动响应谱矩及方差的解析解奠定了基础。

4 地震动响应谱矩的解析表达式

(31)

对式(31)进行积分运算

(32)

由随机振动理论，混合基础隔震耗能结构响应的0阶谱矩等于其方差，比较式(28)及(32)，可验证本文方法的正确性。同时，由随机振动理论可知，动力平稳响应的2阶谱矩等于其平稳响应变化率的0阶谱矩。因此，混合基础隔震耗能结构响应的2阶谱矩可由其变化率的0阶谱矩表示

(33)

混合隔震耗能结构动力响应一阶谱矩为

(34)

对式(34)积分

(35)

由文献[26]可知，2阶谱矩存在，则1阶谱矩必定存在，故存在如下关系

(36)

而实际上振动的频域值必定是有限的，故：

(37)

(38)

根据式 (32)、(33)及(38)，混合基础隔震结构地震动响应的0-2阶谱矩均有简明的解析解。

5 耗能结构的体系动力可靠度

结构动力可靠度的分析方法主要有穿越方法、Monte Carlo模拟方法和扩散方法[27-29]。Monte Carlo模拟方法是公认的计算精度高但存在计算耗时极大的问题；扩散方法目前仅能适用于低纬问题；穿越方法则是研究和应用最多的一类方法。Vanmarcke基于Markov分布假设提出平稳激励的动力可靠度灾变函数理论公式

(39)

式中：ζX为参数X的安全界限值；qX为谱参数。其计算为

(40)

则构件的动力可靠度为

PΧ,s=exp[-Th(ζX)]

(41)

式中，T为一次动荷载的激励时间。

对于剪切型多层结构体系的动力可靠度，可根据欧进萍提出了“最弱失效模型”的串联失效模型，则结构体系的动力失效概率Pf为[30]

(42)

6 算 例

4层钢筋混凝土框架结构，底部设置隔震层和黏弹性阻尼器。结构层力学参数：质量均为4×105kg；刚度均为1.0×108N/m;层高均为3.6 m；阻尼比为0.05。隔震层力学参数：质量为5×105kg，抗侧刚度为2.5×106N/m，阻尼比0.1。抗侧黏弹性阻尼器力学参数：λ=0.05 s；CV=5.5×105Ns/m。地震烈度为8度，三类场，设计分组为2组，依据文献[6],地震动参数取值如下：场地土特征周期Tg=0.4 s,ωg=15.71 rad/s，ξg=0.8 rad/s，ωf=0.15ωg，ξf=ξg，功率谱系数S0=111.34×10-4m-2/s3。

6.1 本文方法验证

由式(3)可知，

(43)

(44a)

(44b)

(44c)

(44d)

式中，强度系数λj,i=uj,iηi，见表1。

表模态强度系数表

(45)

式中：

(46)

(47)

图对比图

6.1.2 谱矩的对比分析

为验证本文计算结构响应0-2阶谱矩的正确性，利用式(32)、(33)及(38)对结构各层位移的谱参数进行计算，并与虚拟激励法进行对比，见图3～图5。虚拟激励法在计算谱矩时为数值积分，为此给定频域变量ω的积分区间为[0,1 000]，积分步长 Δω=0.1 rad/s。

图3 结构各层位移0阶谱矩对比图

从图3～图5可知，本文方法与虚拟激励法在计算0-2阶谱矩时非常吻合，说明本文方法是正确的。此外，本文方法的CPU耗时为0.017 s；虚拟激励法的耗时为4.45 s，本文方法耗时仅为虚拟激励法的1/260，说明了在相同的条件下本文方法可有效提高计算效率。

图4 结构各层位移1阶谱矩对比图

图5 结构各层位移2阶谱矩对比图

6.2 混合基础隔震结构减震效果分析

为验证混合基础隔震结构中黏弹性阻尼器的减振效果，对比分析有无黏弹性阻尼器的结构层间位移的0-2阶谱矩，具体见图6～图11。从图6～图8可知，在基础隔震层增加黏弹性阻尼器相对于基础隔震结构，可有效降低各层相对于地面的侧移的0-2阶谱矩，即可有效限制各层相对于地面的位移、速度(0阶谱矩对应的是结构相对于地面的位移方差；2阶谱矩对应的是结构相对于地面的位移变化率方差)。与基础隔震结构相比，从图9可知，混合耗能结构的各层层间位移会有所降低(0阶谱矩对应的是结构的层间位移方差)；从图10可知，混合耗能结构的1阶谱矩会少量增加；从图11可知，混合耗能结构的位移变化率响应会有一定的增加(2阶谱矩对应的是结构的层间位移变化率方差)。总之，混合耗能结构能有效抑制结构层位移，同时少量降低结构的层间位移。

图6 结构各层位移0阶谱矩对比图

图7 结构各层位移1阶谱矩对比图

图8 结构各层位移2阶谱矩对比图

图9 结构各层层间位移0阶谱矩对比图

图10 结构各层层间位移1阶谱矩对比图

按照现行抗震规范对多遇地震下的层间弹性角取值为1/550，一次动荷载持时为15 s，混合基础隔震结构的体系失效概率为为4.6×10-6；基础隔震结构的体系失效概率为7.34×10-6，可靠度明显提高。

图11 结构各层层间位移2阶谱矩对比图

7 结 论

本文就基础隔震结构+抗侧黏弹性阻尼器组成混合耗能结构基于C-P谱的随机激励下的地震位移，速度及其层间位移和层间位移变化率等工程抗震设计参数的方差及其0-2谱矩的解析解进行了系统研究，提出了一种新的简明解法，结论如下：

(1) 运用C-P谱的等价滤波方程重构混合基础隔震结构的地震动方程，可将基于表达式复杂的C-P谱的地震动转化为易获得简明解的白噪声地震动，运用复模态方法及随机振动理论将耗能体系系列动力响应的功率谱表述为圆频率与耗能体系特征值平方和导数的线性组合，进而获得结构地震动响应方差和谱矩的简明解析解。因此，本文方法适用于线性结构或线性耗能结构基于具有滤波方程的平稳激励的随机地震动响应分析。

(2) 在基础隔震层设置其抗侧作用的黏弹性阻尼器能显著改善基础隔震结构侧向位移过大的问题，但层间位移可能会增大或者变小，需要合理确定黏弹性阻尼器的阻尼系数和松弛时间。

(3) 本文获得了混合基础隔震结构的层间位移0-2阶谱矩的简明封闭解，有助于基于Markov分布假设的动力可靠度分析。