单边周期环形谐振径向声子晶体结构

吕锐翔， 李丽霞， 杨继博

(西安建筑科技大学 机电工程学院，西安 710055)

众所周知，盘类结构广泛应用于机械、电子、纺织、冶金、采矿、汽车、航空、航天及船舶等领域，随着现代科学技术的飞速进步，要求机械装备向低噪声、振动小，或轻型、高精度方向发展，而盘类结构通常是振动能量的载体或者传播体，其结构形式、动态特性及动态激励力的传递方式，对整个系统的振动有重要影响。目前对于盘类结构的减振主要是通过提高其加工精度、控制原材料的质量或通过阻尼减振等。而往往这些方法会增加盘类结构的加工成本和加工难度，同时对于低频振动的隔离常难以奏效。所以，如何在现有的基础上，引入新技术进一步降低盘类结构的振动是十分必要的。

在特定方向上具有周期性的结构对于特定频率段内的弹性波传播具有抑制作用，其可以对盘类结构在特定频率段的振动进行控制[1-3]。声子晶体理论使得周期结构的减振特性得到了进一步的发展[4-5]。目前对于声子晶体其带隙的机制解释主要有两种，一种是布拉格散射(Bragg)机制[6]，另一种是局域共振机制[7]。其中基于局域共振机制的声子晶体相对于基于布拉格散射机制的声子晶体可以在相对较小的晶格常数下得到更加低频的带隙，从而达到对结构低频振动的控制。本文将声子晶体理论引入到工业应用中常见的盘状结构，设计出具有低频减振特性的径向声子晶体结构，有助于实现对盘状结构低频振动的抑制。

Torrent 等[8-10]将声子晶体理论引入到径向周期结构中，设计出一种在径向上具有周期性的径向声子晶体结构，同时验证了其存在的声学带隙。随后Xu等[11-13]将径向声子晶体推广到振动控制领域，得到了基于布拉格机制的弹性波带隙，理论上验证了其对于盘状结构振动的控制。进一步Li等[14]基于Lamb理论研究了周期性波纹的径向声子晶体结构，得到了大于20 kHz的高频带隙。An等[15]研究了一种在径向以及周向上具有周期性的广义径向声子晶体结构，得到了中心频率位于16 kHz的高频宽带隙。由于实际工程中对于振动的控制多在低频时，上述研究虽然在理论上得到了其结构的带隙，但由于其带隙位于高频处，并不能在目前的工业领域得到应用。对Shi等[16-18]提出了基体盘由两种材料在径向上以特定的宽度周期性排列，得到了相较低的带隙。随后Li等[19]研究了在环氧树脂和铝交替排列组成的基体盘上周期性附加散射体的声子晶体结构，得到了低于500 Hz的带隙。Gao等[20]通过在硅橡胶和铅这两种材料沿径向周期排列的基板盘上附加橡胶散射体得到了低于10 Hz的低频带隙。虽然上述研究将带隙降低至1 000 Hz以内，但是其基体盘是通过两种材料组合而成，使得其结构在现有的加工条件下应用于工业领域中难以保证其对于复杂工况的适应，同时基体盘不同材料连接处的易断性使其无法确保工业设备的稳定运行。

1 模型和计算方法

研究提出的新型环状谐振径向声子晶体结构如图1所示，其中图1(a)是5个单位晶格结构沿径向方向周期排列并且绕Z轴旋转得到的三维实体模型，图1(b)单位晶格结构图,图1(c)径向声子晶体结构的形成方式。如图1(b)所示单位晶格结构是由A、B、C三部分组成， A部分宽度为晶格常数。其结构几何参数如下：其中A部分宽度为a，高度为m、B部分宽度为d，高度为c、C部分宽度为b，高度为h，同时C部分距基板距离为n，基板距Z轴距离为r0。

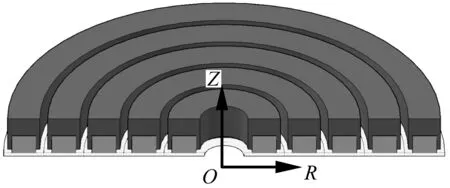
(a) 径向声子晶体盘三维模型

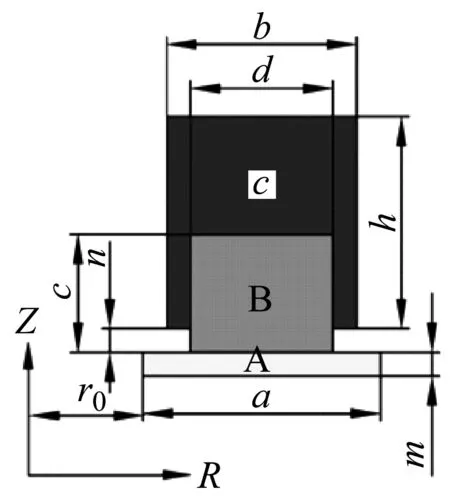
(b) 晶格结构

(c) 径向结构形成方式

为了研究所提出的径向声子晶体结构的振动特性，本文从无限周期结构的能带图，有限周期结构频响函数曲线，本征位移场三个方面进行研究。理论上由于结构在径向方向上具有无限周期，因此根据Block定理，只需研究单个周期的晶格结构，其中单个晶格结构在径向方向的周期边界条件可以表示为

u(r+ra,z)=u(r,z)eikrra

(1)

式中:r是径向位置;a是晶格常数;kr是在径向方向上Bloch波矢量的分量。研究通过改变第一布里渊区边界的k值，来求解特征值问题。本文从有限元软件COMSOL Multiphysics5.2中的特征频率求解器模块的参数扫描函数扫描在R方向上k=0到k=1总共11个细分点，可以得到每个点的固有频率，进而得到所提出的新型环状谐振径向声子晶体结构的能带结构图。

对于有限周期结构，通过计算其频响函数曲线来描述其弹性波传播特性，本文研究了在径向方向上由有限个单位晶格组成的周期阵列结构。通过在有限周期结构的一端沿某一方向施加一定范围频率的加速度激励，同时在其另一端拾取其单个频率的加速度响应，频响函数定义为通过有限周期结构的拾取端加速度响应与激励端加速度激励之比，其数学表达式为

T=20lg(a2/a1)

(2)

式中,a1代表激励端的加速度激励a2代表拾取端的加速度响应。通过改变激励端加速度频率获得其频响函数曲线。

2 带隙及机理分析

为了进一步研究径向声子晶体的带隙特性，本文给出了晶格结构具体几何参数如表1所示，同时给出了其晶格结构所组成的三部分的材料参数如表2所示，其中A部分的基板材料为环氧树脂，B部分的弹性材料为硅橡胶，C部分的质量块为钢。

表1 径向声子晶体晶格结构参数

表2 径向声子晶体结构材料参数

径向声子晶体能带结构图如图2(a)所示，从图中可以看出结构1在0～600 Hz区间内有5条能带，并且在第一和第二能带之间产生了一个位于0.016～0.082(56.5～246.91 Hz)的低频宽带隙。为了进一步验证所提出径向声子晶体其所产生带隙的准确性，分别计算了5个周期下的二维轴对称模型径向以及轴向激励下的频响函数曲线图，同时计算了5个周期下的三维模型轴向激励下的频响函数曲线图，如图2(b)所示。从图中可以看出，在加速度激励下，计算所得到的二维轴对称模型与三维实体模型在的频响函数曲线的带隙范围吻合，并且其与无限周期能带结构图中的带隙吻合，进一步验证了所提出的径向声子晶体结构其带隙的准确性。

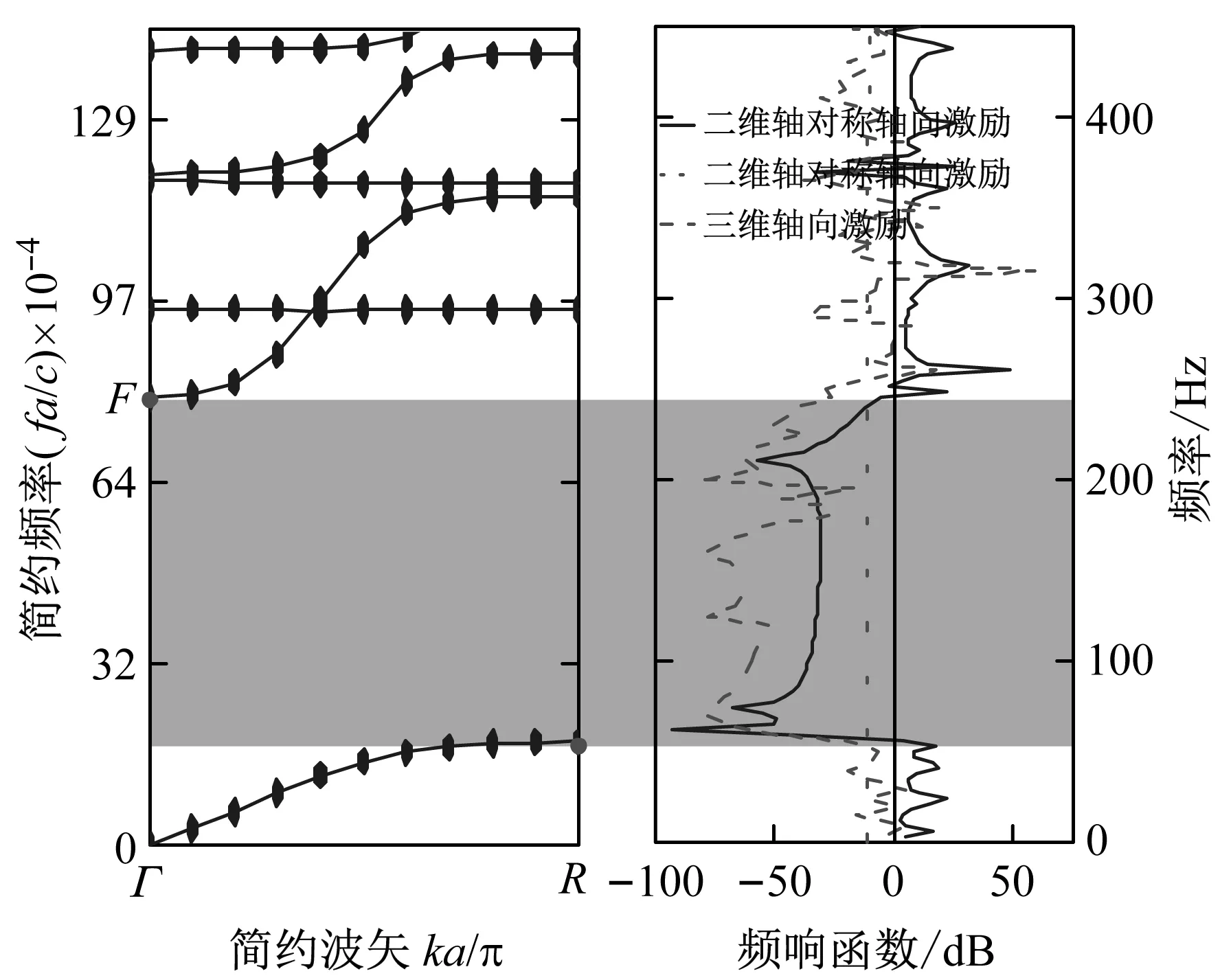
(a) 晶格的能带结构 (b) 有限周期结构频响曲线

为了进一步探讨带隙的产生机制，给出了能带结构图中带隙上下边界处特殊点的本征位移场，如图3所示。从图3中可以看出在E点，也就是带隙的起始频率处。结构的振动主要为基板上部C部分质量块的垂直振动(Z方向)，同时引起了弹性材料B部分的垂直振动(Z方向)，进一步传递到基板上。这是由于结构由三种材料组成，并且每种材料的固有频率不同，当激励频率接近质量块的固有频率时，引起了质量块在垂直方向的振动，此时质量块沿垂直方向通过弹性软材料硅橡胶传递给基板一个作用力，其传递力的大小与质量块的质量和弹性软材料的刚度成正比，进而抑制了基板的振动，使得弹性波不能在基板中传播。在带隙范围内，图3(a)E点始终保持为主振型，其作用力持续在基板上，基板的振动持续被抑制。根据模态叠加原理[21]。

x=ηA1+ηA2+…+ηAn

(3)

式中：x表示响应；ηAn表示模式An的参与系数。随着激励频率逐渐接近质量块的固有频率时，模式A1的放大系数逐渐增大，其参与系数ηA1随之增大，振子的振幅随之上升，同时使得作用在基板上的作用力逐渐增大，直到抑制基板的振动，过程如图4所示。图4为能带结构图中第一频带上K从0～1所有点的本征位移场。随着激励频率的增大，逐渐远离质量块的质量块的固有频率时，放大系数变小使得参与系数ηA1逐渐降低，质量块的振动方向与E点相反。此时基板与质量块在垂直(Z方向)反向振动，进而压缩了B部分的硅橡胶，此时F点转换为主振型，如图3(b)所示，带隙截至。

(a) E点

(b) F点

图4 第一能带所有点的本征位移场

进一步，本文给出了对比模型2和3，其晶格结构的几何参数与模型1一致，其中模型2的B部分材料为硅橡胶，C部分材料为环氧树脂，模型3是将模型1中A部分的材料由原始的环氧树脂变为钢。本文分别计算了模型2和模型3的能带结构图，如图5所示，其中图5(a)为模型2的能带结构图，图5(b)为模型3的能带图。从图中可以发现，当质量块为与基板材料相同的质量较轻的环氧树脂时，相对于质量块为钢的能带结构图，带隙的起始频率和截至频率均有升高，并且起始频率有较大的上升。但是对于仅仅将A部分的材料更换为钢，其带隙的范围为58.58～137.8 Hz。带隙的起始频率几乎保持不变，而截至频率发生了较大的下移。对于带隙起始频率和截至频率可以理解为等效质量弹簧系统，同时可以由下式确定。

(4)

(5)

式中:f1为起始频率;f2截止频率;K1为等效弹簧的刚度;M1为其振子的质量;M2为其基板以及弹簧的质量。

(a) 模型2

(b) 模型3

对于本文所提出的声子晶体盘状结构，其振子质量M1为C部分的质量，等效弹簧为B部分的刚度。对于模型2，其C部分为环氧树脂，而其它参数不变，相对于模型1，C部分质量M1减少，由式(4)可知带隙起始频率增大。而对于截止频率，由式(5)可知，由于M1的质量远远大于M2的质量，因此当M1减小，其截至频率变化较小。而对于模型3，由于B部分以及C部分均为发生改变，因此对于起始频率由式(4)可知，带隙起始频率几乎不变。而对于截至频率，由式(5)可知，M2发生较大的增加，因此截至频率出现较大的下移。

3 参数对带隙的影响

3.1 基板厚度m对带隙的影响

为了验证带隙的截至频率是由于基板质量的大小所影响，本文在仅改变A部分基板的厚度m时，分别计算了其带隙范围，其计算结构如图6所示。从图中可以看出，随着m的增加，带隙的起始频率几乎保持不变，但是截至频率随着m的增加而降低。这是由于基板A部分在截至频率处的振型在垂直(Z)方向，随着厚度m增加，基板A的质量在增加，这也与上文中基板材料为钢时，带隙的截止频率大幅降低一样。为了进一步验证仅仅是基板的质量对带隙的截止频率产生影响，本文计算了在基板为环氧树脂时，其在宽度a不变时仅仅改变基板厚度m的带隙范围。钢的密度为7 890 kg/m3，环氧树脂的密度为1 180 kg/m3，由于宽度不变，因此基板为环氧树脂时，其基板厚度m为26.7 mm，因此选取基板厚度m为27 mm，计算得到其带隙位于59.17～136.6 Hz，结果与基板为钢，厚度为4 mm时的带隙范围基本吻合。

图6 基板厚度m对带隙的影响

3.2 钢块高度h对带隙的影响

进一步分析了在其它参数不变时，仅改变C部分质量块的高度h时，分别计算了其带隙范围，其计算结构如图7所示。从图中可以看出，随着质量块高度的增加，带隙的起始频率在降低，而截至频率基本保持不变。这是由于随着质量块高度的增加，其振子质量M1随之增加，由式(5)可知，带隙的起始频率降低。而对于截止频率，由于M1的质量远远大于M2的质量，因此当M1增大时，由式(6)可知截至频率仅有较小的降低。

图7 钢块高度h对带隙的影响

3.3 橡胶的高度c对带隙的影响

最后分析了在其它参数不变时，仅改变B部分橡胶块的高度c时，分别计算了其带隙范围，其计算结构如图8所示。从图中可以看出，随着橡胶块高度的增加，带隙的起始频率保持不变，截止频率逐渐降低。这是由于随着橡胶的高度c的增加，M2随之增加。由式(5)以及式(6)可知带隙的起始频率不变，截至频率逐渐降低。

图8 橡胶的高度c对带隙的影响

4 结 论

本文研究了新型环状谐振径向声子晶体结构的带隙特性，分析了其晶格结构参数对带隙特性的影响，其结论如下：

(1) 新型环状谐振径向声子晶体结构在基板材料为一种时，具有低频宽带隙特性，相比于传统的径向声子晶体，其基板材料的单一使得其结构在工业应用中更加的稳定。

(2) 基板以及橡胶块的高度对带隙的截止频率有较大的影响，对带隙的其实频率几乎没有影响。而质量块的高度决定着带隙的起始频率大小，但是其影响较小，同时其对于截止频率几乎无影响。因此可以在对带隙范围影响较小时，通过降低质量块的高度，增加基板的厚度，来进一步增加结构整体的稳定性。