证明时空Rn的最大维度是4

李玉发 李宇航

1．广东省惠州市第一中学 广东 惠州 516001;2．澳大利亚国立大学硕士研究生精算专业2019届

(1)易点宇航法则:J4n＋k＝ik(n,k∈N,k≤3)

(2)航易方程:1＋J24n＋m＝0,J4n＝1,J4n＋m＝Jm,n∈N,m∈N＋,m≤3

(3)H(航)－F(发)无限数维有限类形结论:

①Rn⊆R4,②Rn的最大维度是4唯,③Jn的最大维度是3唯

一、基本原理[1]

定义1n维的时点Pn＝(x0,x1,···,xn－1)(n∈N＋,xk∈R,k∈N),P0＝(x0)＝x0

定义2 零点On:O0＝Φ,O1＝(0)O2＝(0,0),O3＝(0,O2),…,On＝(0,On－1)．

定义3 数光点Tn:T1＝(1),T2＝(0,1),T3＝(0,0,1),…,Tn＝(On－1,1)．

形光点Jn:J0＝(1),J1＝(0,1),J2＝(0,0,1),…,Jn－1＝(On－1,1)．

有结论:Tn＋1＝Jn(n∈N)

定义4 升维:(n,k∈N,xk∈R,)

1)x0＝(x0)＝(x0,0)＝(x0,02)＝(x0,0k)．

2)(x0,x1)＝(x0,x1,0)＝(x0,x1,02)＝(x0,x1,0n)．

3)(x0,x1,···,xn)＝(x0,x1,···,xn,0)＝(x0,x1,···,xn,0k)．

定义5 关于形时空间Jn与数时空间Tn,有

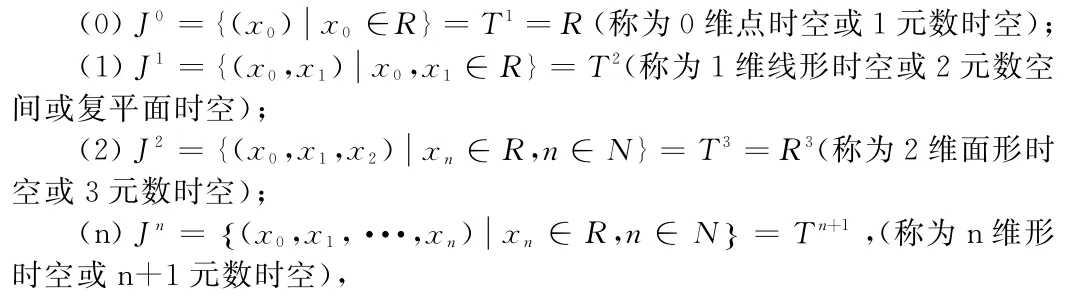
当n＝4m＋j,m∈N,j＝0(1,2,3),Jn是m级的点(线,面,体)形时空．

二、具体应用

定义6 易点列Tn:T0＝On,T1＝(1),T2＝(0,1)＝(0,T1),T3＝(0,0,1)＝(0,T2),

——,Tn＋1＝(On,1)＝(0,Tn)。(n∈N∗)(↔ 表示一一映射)则有

1)一维实点T1＝(1)＝(1,On)↔1,实数J0＝i0＝1↔T1。

2)二维复点 (x,y)↔x＋yi,x,y∈R,i2＝－1,i－1＝－i

T2＝(0,1)↔0＋i＝i,复数J1＝i1＝i↔T2。

T3＝(0,T2)↔(0,J1)＝0＋J1i＝ii＝i2＝J2＝－1,复数J2＝i2＝－1↔T3。

T4＝(0,T3)↔(0,J2)＝0＋J2i＝i3＝J3＝－i,复数J3＝i3＝－i↔T4。

T5＝(0,T4)↔(0,J3)＝0＋iJ3＝ii3＝i4＝J4＝－1,复数J4＝i4＝1↔T5。

定义7 易点列Tn:T0＝On,T1＝(1),T2＝(0,1),T3＝(0,0,1),

——,Tn＋1＝(On,1)＝(0,Tn)。(n∈N∗)(↔表示一一映射)

则有(易点的虚－－－实法则):

1)实数1↔T1＝(1),实数1＝J0＝i0＝T1。

2)虚数i＝J1↔(0,1)＝T2,虚数i＝J1,i2＝－1,i－1＝－i。

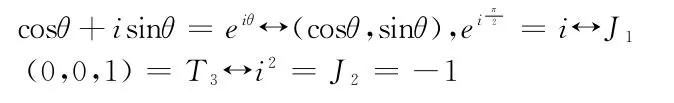
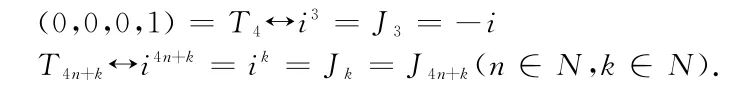
定义8 (发易FT法则):

(1)易点列Tn:Tn＝(0n－1,1)(n∈N∗),(↔ 表示一一映射)则。

易点列T1＝(1)↔1＝i0,T2＝(0,1)↔i,T3＝(0,0,1)↔i2,

——,Tn＝(0n－1,1)↔in－1

(2)发点列Fn＝(in－1)＝in－1T1(n∈N∗),则Fn＋1＝iFn。则Fn＝Tn(n∈N＋)

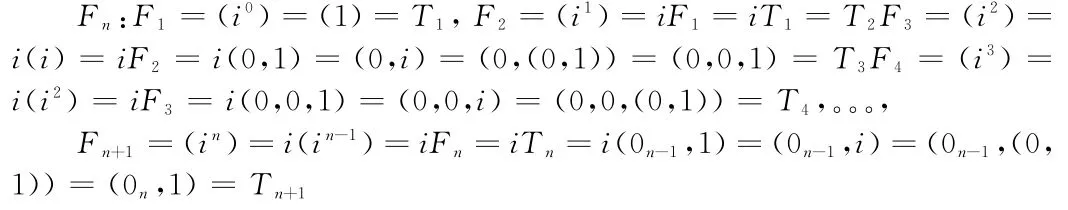
结论1[2]:

(1)易点宇航法则 :J4n＋k＝ik(n,k∈N,k≤3)

(0n,1)↔Jn,n∈N,虚数i满足:i↔(0,1),i2＝－1

J0＝i0＝1↔(1)＝T1,J0称是点量,

J1＝i1↔(i)＝iT1＝T2,J1称是线量,

J2＝i2↔(i2)＝i2T1＝T3,J2称是面量,

J3＝i3↔(i3)＝i3T1＝T4,J3称是体量,

Jn＋1＝iJn＝iin＝in＋1↔(0n,i)＝i(0n,1)＝iTn＋1＝in＋1T1,称Jn是易量,综合上面易点的宇航法则:J4n＋k＝ik↔Tk＋1＝ikT1(n∈N,k∈N＋)

(2)航易方程:1＋J24n＋m＝0,J4n＝1,J4n＋m＝Jm,n∈N,m∈N＋,m≤3

(3)宇航易点方程(n∈N＋,m∈N)

易点有五大类:T0＝On＝Φ(0维的原点),T4n＋1＝T1(一维线点)T4n＋2＝T2(二维面点) ,T4n＋3＝T3(三维体点),T4n＋4＝T4(四维时点)。

T4n＋m＝Tm,T4＋0＝T0⇒结论:4维的时点＝0维的原点

定义9 (n,m∈N)(m∈N,m≤3)

(1)易量有五大类

J4n＝J0＝i0＝1(0维的点)↔T1,J4n＋1＝J1＝i(1维的线)↔T2,

J4n＋2＝J2＝i2＝－1(2维的面)↔T3,J4n＋3＝J3＝i3＝－i(3维的体)↔T4。

J4n＋4＝J4＝i4＝1(4维的时间)↔T5

Jm＝im(m维的易量)↔Tm＋1

(2)易量的运算法则:

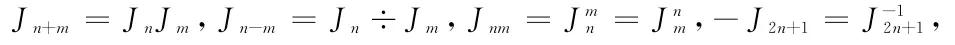
(3)J4n＋m＝Jm,J4＋0＝J0⇒结论:4维的时间＝0维的点元

(4)易量与易点的转换法则:(↔表示一一映射)

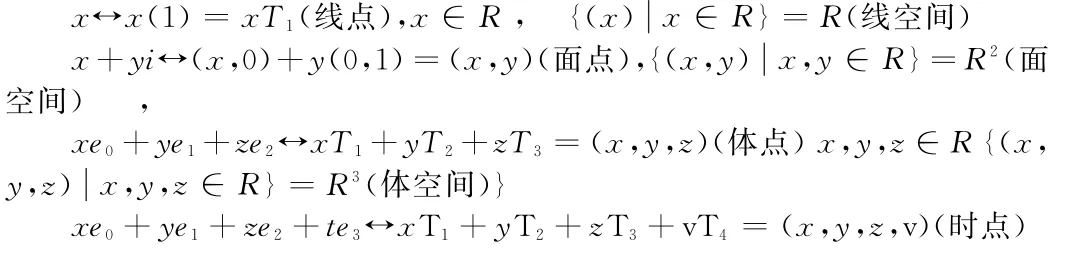
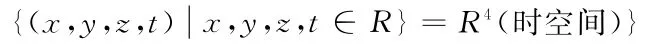
定义10 [Rn升降维法则－－－F(发)升维法则]

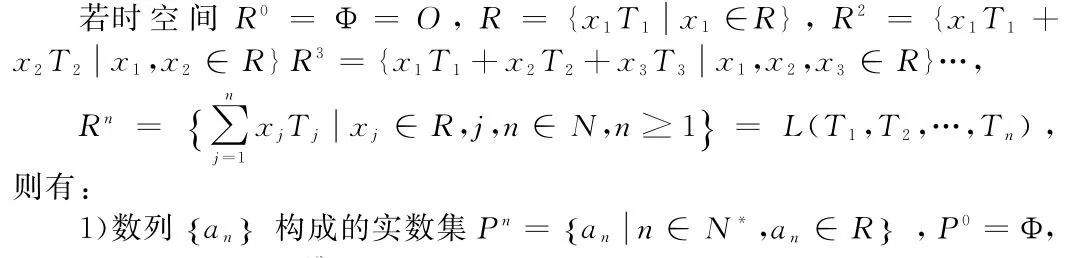
称P0＝Φ为0维(极)空间,称Pn为0维(点)空间

2)R＝(R,0)⊆R2,称R为1维(线)空间

3)R2＝(R2,0)⊆R3,称R2为2维(面)空间

4)R3＝(R3,0)⊆R4,称R3为3维(体)空间

5)R4＝(R4,0)⊆R5,称R4为4维(时)空间

6)Rn＝(Rn,0m)⊆Rn＋m(n,m∈N)

定义11 向量空间维数的定义

在线性点空间V中,如果存在n个点A1,A2,···An,满足:

(i)A1,A2,···An线性无关;

(ii)V中任一元素A总可由A1,A2,···An,线性表示．

那么,A1,A2,···An,就称为线性空间V的一个基,n称为线性空间V的维数．

维数为n的线性空间称为n维线性空间,记作Vn,．

称为n维线性空间Vn由基底A1,A2,···An所生成。