时间序列分析模型在黄海南部小黄鱼资源量预测中的应用
宋大德,汪金涛,陈新军,仲霞铭,熊瑛*,汤建华,吴磊
( 1. 上海海洋大学 海洋科学学院,上海 201306;2. 江苏省海洋水产研究所,江苏 南通 226007)
1 引言
小黄鱼(Larimichthys polyactis)属硬骨鱼纲(OSTEICHTHYES)、鲈形目(Perciformes)、石首鱼科(Sciaenidae)、黄鱼属(Larimichthys),广泛分布于东海、黄海和渤海近底层水域,也是中、日、韩三国共同利用的主要经济鱼种,在我国近海海洋渔业中具有重要的地位,曾为我国“四大渔业”之一[1]。20 世纪50-80 年代,小黄鱼资源经历了从成熟期到衰退期的演变,主要由于70 年代后捕捞强度增大和环境恶化的影响。20 世纪90 年代后,我国实施了禁渔期、禁渔区和保护区等系列手段以保护小黄鱼的产卵场和补充群体,其资源得到了有效保护[2],产量逐年上升。21 世纪以来,小黄鱼产量处于居高不下的态势,与之相伴随的是小黄鱼低龄化、小型化和性成熟提前等日益凸显的特征[3–4],如若不及时控制捕捞强度改变此种状况,小黄鱼渔业很有可能面临崩溃的风险[5–6]。因此,基于长周期的资源监测调查对小黄鱼资源动态进行研究,明确其资源量以有效控制捕捞强度,对当前渔业管理具有重要的参考意义。
迄今为止,在小黄鱼资源评估方面缺乏较为系统的定量研究[7–11],且其中大多是采用基于调查设计的方法,用扫海面积法来评估一个年度春、夏、秋、冬四季资源的时空变化;基于模型的评估方法则较少应用,仅见于剩余产量模型、贝叶斯模型等方法[5,12–13]。而在基于模型的方法中,时间序列分析模型相对于静态处理统计方法在分析和处理方面具有无可比拟的优势,随着数值方法和计算机的发展,已经形成了一套完整的分析和预测体系[14],在渔情预报渔获量预测方面已有较好的应用[15–19],且与人工神经网络、贝叶斯模型相比,时间序列分析模型表现出更高的精度[20]。
帆式张网(学名:单锚张纲张网)是黄海南部最主要的捕捞形式之一,其作业原理是根据捕捞对象的生活习性和作业区域的水文条件,将网敷设在海中鱼、虾类等的洄游通道上,依靠水流的作用,迫使捕捞对象进入网囊中;其作业位置并非一直固定不变,而是随着鱼群分布变化而转移作业场所。2008-2015 年《中国渔业统计年鉴》显示,张网类渔具捕捞量仅次于拖网类、刺网类,位居第三位,占我国近海海洋捕捞量的12%~13%;曾有学者用张网渔获监测数据估算东海区小黄鱼总允许渔获量[21]和最大持续产量[12]及分析黄海南部小黄鱼时空分布特征[2],以上研究均已为小黄鱼渔业资源管理提供了积极的指导作用。本文利用2003-2016 年黄海南部帆式张网小黄鱼渔获监测数据,应用时间序列ARIMA(Autoregressive Integrated Moving Average ,ARIMA)模型,对黄海南部小黄鱼资源量进行拟合和预测,旨在为小黄鱼的有效管理和可持续利用提供科学依据。
2 材料和方法
2.1 数据来源
数据来源于江苏省海洋水产研究所2003-2016年1-12 月(伏休期除外)黄海南部帆式张网小黄鱼渔获监测资料。监测船为“苏启渔02420”“苏启渔03203”“ 苏 启 渔02105”“ 苏 启 渔02377”“ 苏 启渔03650”;所用网具为帆式张网,渔具规格220 m×200 m(网口装扎周长×纵向网衣拉直长度),最大网目尺寸700 mm(网口),向后沿纵向依次递减至25 mm(网囊);2003-2016 年黄海南部帆式张网监测船数、航次数和总投网次数详见表1。监测范围涉及黄海南部吕泗渔场、大沙渔场、长江口渔场以及沙外渔场和江外渔场紧邻125°E 的我国渔船可生产海域(图1)。
2.2 数据分析
2.2.1 数据处理
单位捕捞努力量渔获量(Catch Per Unit Effort,CPUE)为每年小黄鱼渔获量除以相应投放网口数,以该CPUE 值作为黄海南部海域小黄鱼资源的丰度指标[22]。主要运用SPSS24、Eviews8.0 和Arcmap10.4 软件进行数据处理。
采用ARIMA 模型对小黄鱼年CPUE 进行时间序列拟合及预测,该方法的基本思路是:对于非平稳的时间序列,用若干次阶差分使其成为平稳序列,再用ARMA(p,q)对该序列建模。

表1 2003-2016 年黄海南部帆式张网监测船数、航次数和总投网次数Table 1 The number of monitoring vessel by canvas stow net,voyage and hauls from 2003 to 2016 in the southern Yellow Sea

图1 2003-2016 年黄海南部帆式张网调查区域所涉渔场Fig. 1 The fishing grounds surveyed by canvas stow nets in the southern Yellow Sea from 2003 to 2016
2.2.2 ARIMA(p,d,q)模型
一个ARIMA(p,d,q)过程包括自回归项(p)、差分阶数(d)和移动平均项(q),一般情况下,p、d、q各参数的值不超过2,否则会导致数据失真,用数学公式表示如下:
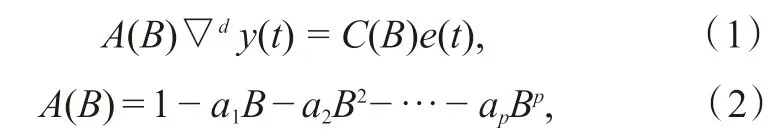
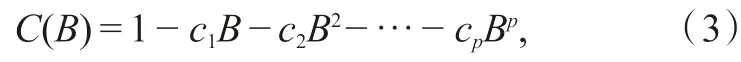
式中,y(t)、e(t)分别表示原序列和白噪声序列;B是滞后算子,满足表达式:Bny(t) =y(t-n),n= 1,2,···,n;▽d= (1 -B)d是d阶差分,d= 1,进行一次差分处理,即令z1(t) = ▽y(t) =y(t) -y(t- 1);d= 2,进行两次差分处理,即z2(t) = ▽2y(t) =▽z1(t) =z(t) -z(t-1),依此类推。
Box-Jenkins 法应用于时间序列建模,预测的过程如下5 个步骤逐级进行:
(1)数据的预处理:包括差分平稳化处理和零均值化处理,这一步骤是使该序列满足时间序列建模的前提条件。
(2)模型结构的辨识:根据不同模型自相关函数(Autocorrelation Function,ACF)和偏相关函数(Partial Autocorrelation Function,PACF)的性质(表2),确定模型的阶数。AR(p)和MA(q)模型的区别在于其所依据的变量不同,AR 模型依据滞后序列进行预测,而MA 模型依据误差数据序列的未来变化进行预测;多数情况下这两种模型需要结合使用,就形成了ARMA(p,q)模型。上述3 种模型都是基于平稳的时间序列建立的,当时间序列数据不平稳时,就需要用到ARIMA(p,d,q)模型对数据预处理,如步骤(1)。表2 中,拖尾是指ACF 或PACF 随着时滞k的增加呈现指数衰减并趋于0,而截尾则是指ACF 或PACF 在某步之后全部为0。

表2 4 类模型的相关函数性质Table 2 The correlation function properties of four types of models
(3)模型参数估计:本文采用最小二乘法估计模型的参数,最小二乘法就是根据一组X和Y的观测值,选择Y的逼近函数f(xi;b,c,···)使得偏差的平方和最小,确定逼近函数中的参数b,c,···,以确定Y和X之间的经验关系。如下式:

式中,b和c1,c2,···,ci代表常数。
(4)模型检验:通过对原时间序列与所建模型之间误差序列是否有随机性的检验来实现;若模型检验不能通过,则需要回到步骤(2)重新进行模型结构的鉴别。
(5)模型预测:利用所建立的合适模型导出其预测模型,应用于实际预测。
3 结果
3.1 时间序列的平稳性检验
对水平序列、一阶差分序列和二阶差分序列进行单位根检验,结果如表3。

表3 水平序列和差分序列单位根检验表Table 3 Unit root test of horizontal sequence and difference sequence
从表3 中可以看出,水平序列的单位根检验t值为-2.766 2 明显大于其1%水平值,水平序列存在单位根,所以水平序列不平稳。经过一阶差分后的序列t值略微小于其1%水平值。经过二阶差分后的序列t值明显小于其1%水平值。初步判定模型为ARIMA(p,2,q)模型。
3.2 时间序列的ACF 和PACF 图
运用SPSS 软件,绘制出二阶差分序列的ACF 和PACF 图(图2),由图2 中ACF 图可以看出:当延迟期数大于1,其自相关系数位于置信度区间内,因此黄海南部2003-2014 年小黄鱼年CPUE 二阶差分序列的自相关系数是1 阶截尾的。由PACF 图可以看出其系数值都处在置信度区间内,处于拖尾状态,因此ARIMA 模型的q值为0。对本研究序列建立ARIMA(1,2,0)和ARIMA(2,2,0)。
3.3 ARIMA 模型拟合及检验
利用SPSS 对模型ARIMA(1,2,0)和ARIMA(2,2,0)进行拟合,运行结果显示:ARIMA(1,2,0)模型贝叶斯信息准则(Bayesian Information Criterion,BIC)值为6.031,ARIMA(2,2,0)模型BIC 值为6.345。依据贝叶斯信息准则,ARIMA(1,2,0)模型拟合的效果较好。利用最小二乘法法对ARIMA(1,2,0)模型进行参数估计(表4)。由表3 得其数学表达式为:yt=-0.714 - 1.006yt-1+et。
通过观察模型的残差ACF、PACF 图(图3)检测模型适应性,从图3 中分析可知,残差自相关函数和偏相关函数均落在置信区间内,残差序列为白噪声过程。因此,用该模型拟合得较好,可将原时间序列中所蕴含的相关性充分提取出来。综上分析,可确定ARIMA(1,2,0)为最佳模型。

图2 二阶差分序列的自相关函数(ACF)和偏相关函数(PACF)图Fig. 2 The ACF and PACF diagrams of second order difference sequence

表4 ARIMA(1,2,0)模型参数估计表Table 4 The parameter estimation of the ARIMA (1, 2, 0) model

图3 ARIMA(1,2,0)模型残差序列自相关函数(ACF)和偏相关函数(PACF)图Fig. 3 The ACF and PACF diagrams of the ARIMA (1, 2, 0)model residual sequence
3.4 ARIMA 模型预测
运用ARIMA(1,2,0)模型,对2003-2014 年黄海南部小黄鱼年CPUE 时间序列进行拟合,结果如图4,拟合值与实际值相关系数为0.881,且相关性显著(p<0.05)。对2015-2016 年黄海南部小黄鱼年CPUE值进行预测,模型预测值分别为47.66 kg/网和49.16 kg/网,与实际值51.10 kg/网和40.05 kg/网的相对误差分别为6.73% 和22.75%,总体相对误差为14.74%。因此,可说明运用ARIMA(1,2,0)模型能有效地对黄海南部小黄鱼年CPUE 拟合和预测。

图4 2003-2014 年黄海南部小黄鱼年CPUE 模型拟合值与实际值关系Fig. 4 The relationship between simulated and actual CPUE of small yellow croaker in the southern Yellow Sea from 2003 to 2014
4 分析与讨论
2003-2016 年黄海南部帆式张网的监测数据显示,小黄鱼年CPUE 值的变化趋于平稳,表明近14 年小黄鱼渔获产量并没有出现下降的态势。这与《中国渔业统计年鉴》中江苏海域小黄鱼产量一直居高不下的趋势一致,亦与严利平等[23]在小黄鱼资源研究中认为“小黄鱼资源自20 世纪90 年代后半期以来处于稳定丰厚期”的结论一致,究其原因:其一,高强度捕捞是造成黄海小黄鱼渔获量较高的主要因素[24];其二,我国政府自1995 年以来实施伏季休渔制度并不断调整优化,并于2010 年设立“吕泗渔场小黄鱼银鲳国家级水产资源保护区”等举措对小黄鱼资源起到增殖效果[2,23];其三,张吉喆[25]认为中韩两国2001 年签署的《中华人民共和国政府和大韩民国政府渔业协定》,对小黄鱼资源也起到了很好的养护作用;其四,小黄鱼1 龄鱼性成熟比例和个体绝对繁殖力显著提高,这对小黄鱼的资源补充能力提升起到了关键作用[6]。过度捕捞是诱导小黄鱼生命史特征演变的关键因素,许多开发性鱼类资源因过度捕捞而衰退甚至枯竭[26]。鉴于此,应加强小黄鱼资源评估,选取最优模型和参数配置对管理措施下的现行资源状况进行正确评估和精准预测,以确保真正实现渔业资源种群结构的好转和合理化。
通过比较扫海面积法、剩余产量模型、贝叶斯模型和时间序列模型在小黄鱼资源评估上拟合和预测效果,逐一分析了各类评估方法和模型使用时的缺陷,以及影响评估效果的因素。采用扫海面积法评估小黄鱼资源状态的文章较少,林龙山[8]曾用扫海面积法对东海区小黄鱼资源量进行估算,但实际产量与估算结果相差较大;关丽莎等[27]曾用扫海面积法和地阶广义线性混合模型分别对黄海南部小黄鱼资源量进行评估,结果表明模型估算精度比扫海面积法估算的要高。分析其原因认为,扫海面积法中所使用小黄鱼的可捕系数不仅受其昼夜垂直移动特征影响[27],还与栖息水域、首次性成熟年龄[28]以及个体大小[29]等有关。
多数研究者采用剩余产量模型对小黄鱼资源状况进行评估,其中参数估计是影响模型预测精度的主要因素,如自然死亡系数M 对生长方程中的参数、生物参考点估计影响较大,进而造成模型预测结果的偏差[30]。林龙山[8]研究2002 年东海区域小黄鱼资源,估算M 值为0.58;周永东等[12]研究1996-2009 年东海区域小黄鱼资源,估算M 值约为0.12;高春霞等[31]研究2016 年浙江南部近海小黄鱼资源时估算M 值为1.34。上述研究中小黄鱼自然死亡系数M 值偏离较大,笔者认为,除调查水域小黄鱼栖息水温因素影响外,更有可能是估算M 值的方程由于调查区域不同、年代变迁等因素出现不适用性。例如,詹秉义等[32]曾在1984 年评估绿鳍马面鲀资源时推导出M 值的线性回归方程,该方程在多种渔业资源群体中一直沿用至今,其中包括小黄鱼群体。基于上述M 值变化的分析,笔者认为该线性方程可能已不适用于当前我国小黄鱼资源群体评估。日本学者田中昌一提出采用年龄数据估算鱼类自然死亡系数 M 值的线性回归方程需要更多的、更新的数据进行及时修正,否则参数设置所得出的评估结果作为渔业管理参考依据将会影响渔业资源可持续利用管理决策的正确性[33]。官文江和吴佳文[34]采用剩余产量模型对印度洋黄鳍金枪鱼资源评估时发现,形状参数很难被估计,而且随着数据时间段变化,形状参数的最佳取值差别很大。使用模型过程中参数估算的不确定性是无法避免的,需采用更为科学准确的方法降低不确定性,此后有学者开始采用贝叶斯方法试图解决这一问题[35–37],贝叶斯方法充分考虑了模型和参数值存在的不确定性,其参数后验分布集合了其他参数所有可能值,因此可以提高模型评估的可信度。
时间序列是一组依赖于时间t 的随机变量,这组随机变量所具有的自相关性和依存关系表征了预测对象发展的延续性,用相应的数学模型近似描述这种相关性,就可以从时间序列的过去值,预测其将来的值[38]。时间序列分析是一种数据驱动的方法,Bakker 等[39]采用多种模型研究地下水流问题时,发现时间序列分析模型较常规评估模型不仅简单,而且拟合效果更好。董江水和诸英富[16]曾基于统计数据用时间序列分析模型对江苏省河蟹总产量进行预测,模型拟合值与实际值的相关系数为0.995,产量预测相对误差为3.8%,相较本文模型拟合与预测结果要高,其原因可能是本文的原始时间序列数据取自固定监测样本船,相较统计数据波动性较大,因此模型的拟合值与实际值间的相关性就会被削弱,致使预测精度下降。但本模型预测精度近90%,进一步表明帆式张网监测船渔获数据适用于时间序列分析模型的预测。
需要注意的是,即使是同一海域、同一物种,同一时间序列数据也不能简单套用时间序列分析模型,不同时间序列数据ARIMA 模型的p、d、q 值不尽一致,应根据相关理论指导和分析,对具体的资料进行详尽分析以确定适宜的p、d、q 值[40]。本文构建的ARIMA(1,2,0)模型通过了适应性检验,能较好地拟合黄海南部小黄鱼资源量的变动趋势,说明时间序列模型用于渔业资源量预测是可行的,但由于ARIMA模型的局限性,在短期预测方面更具优势[38]。

