完美积幻方的定义及其构造

张 婧，刘兴祥，刘娟娟

(延安大学数学与计算机科学学院，陕西延安716000)

近年来，幻方研究者立足于和幻方的研究，使其研究成果[1-16]颇为丰富。而积幻方在幻方中同样占有重要地位，尤其是完美积幻方具备更强的幻性，因此，其应用更为广泛，但还没有展开广泛研究。本文给出一系列完美积幻方的定义，得到一种利用完美和幻方构造完美积幻方的方法，并给出证明和举例。

1 预备知识

定义1[1]设F是数域，矩阵A+(aij)m×m∈Fm×m，如果矩阵A满足：

则称矩阵A为数域F上的m阶积幻方，并称P(A)为m阶积幻方A的幻积。

定义2[2]若矩阵A满足：

1)∀i∈{1,2,…,m}有

2)∀j∈{1,2,…,m}有

Pc；

3)Pc=Pr=

则称矩阵A为数域F上的m阶积幻方，并称P为m阶积幻方A的幻积。

2 主要结果

定义3 设矩阵A=(aij)n×n∈Zn×n，n∈N*，若矩阵A满足以下条件：

5)Pr=Pl=Pm=Pn。

则称矩阵A=(aij)n×n为Z上的n阶积幻方，幻积记为P。

定义4 设矩阵A=(aij)n×n∈Zn×n，n∈N*，记p≡i+u(modn),q≡n+1-u-i(modn)，若矩阵A满足以下条件：

5)Pr=Pl=Pn=Pm。

则称矩阵A=(aij)m×n为Z上的n阶完美积幻方，幻积记为P。

定义5 设矩阵A=(aij)n×n∈{1，2，…，n2}，n∈N*，∀u∈{0，1，…，n-1}，记p≡i+u(modn),q≡n+1-u-i(modn)，若矩阵A满足以下条件：

5)Pr=Pl=Pm=Pn。

则称矩阵A=(aij)m×n为Z上的n阶始元完美积幻方，幻积记为P。

定义6 设矩阵A=(aij)n×n∈{k+1，k+2，…，k+n2}，n∈N*，∀u∈{0，1，…，n-1}，记p≡i+u(modn)，q≡n+1-u-i(modn)，若矩阵A满足以下条件：

5)Pr=Pl=Pm=Pn。

则称矩阵A=(aij)m×n为Z上的n阶连元完美积幻方，幻积记为P。

定义7 设矩阵A=(aij)n×n∈S，n∈N*，其中S={x1,x2,…,xn}，∀i,j{1,2,…,n}，有i≠j，则ai≠aj，∀u∈{0，1，…，n-1}，记p≡i+u(modn)，q≡n+1-u-i(modn)，若矩阵A满足以下条件：

1)∀i,j,k∈{1,2,…，n}，当j≠k时，aij≠aik；

2)∀i,j,k∈{1,2,…，n}，当i≠k时，aij≠akj；

3)∀i,j,∈{1,2,…，n}，当i≠j时，aip≠ajp；

4)∀i,j,k∈{1,2,…，n}，当i≠j时，aip≠ajp。

则称矩阵A=(aij)m×n为Z上的n阶完美拉丁和积幻方，幻和记为S，幻积记为P，且S=P。

定义8 设矩阵A=(aij)n×n∈S，S={b,bq,bq2，…,bqn2-1}，若矩阵A满足以下条件：

5)Pr=Pl=Pm=Pn。

则称矩阵A=(aij)n×n为Z上的n阶等比积幻方，幻积记为P。

定义9 设矩阵A=(aij)n×n∈S，n∈N*，其中S={b,bq,bq2，…，bqn2-1}，∀i，j∈{1，2，…，n}，有i≠j，则ai≠aj，∀u∈{0，1，…，n-1}，记p≡i+u(modn)，q≡n+1-u-i(modn)，若矩阵A满足以下条件：

5)Pr=Pl=Pm=Pn。

则称矩阵A=(aij)m×n为Z上的n阶完美等比积幻方，幻积记为P。

定理1 若矩阵A=(aij)n×n∈Z满足：

5)Sc=Sl=Smd=Scd。

令矩阵B=(f(aij))n×n，其中f(x)=cx，c∈Z，则矩阵B为积幻方。

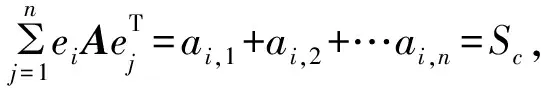
ca1,nca2,n-1…can,1=cScd，

由于Sc=Sl=Smd=Scd，

可得cSc=cSl=cSmd=cScd，则Pr=Pl=Pm=Pn。

证毕。

推论1 若矩阵A是连元和幻方，则矩阵B是等比积幻方。

推论2 若矩阵A是完美和幻方，则矩阵B是完美积幻方。

推论3 若矩阵A是连元完美和幻方，则矩阵B是完美等比积幻方。

3 举例

根据定理1可构造出5阶完美积幻方，如下：

令c=2，则矩阵B=

矩阵B为积幻方，并且为完美积幻方。