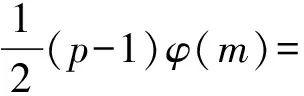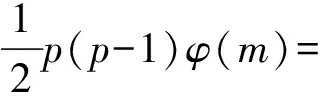广义欧拉函数方程φ2(n)=S(n28)的正整数解

曹盼盼，赵西卿

(延安大学数学与计算机科学学院，陕西延安716000)

20世纪90年代，美国著名的数学家Smarandache提出了许多新的数论问题[1]，并定义了若干新的数论函数，对现代的数论发展产生了较大的影响[2]。其中Smarandache本人命名的Smarandache函数S(n)近年来受到国内外诸多学者的广泛关注和深入研究。

对于欧拉函数方程

φ2(n)=S(nk),n≥2，

(1)

1 相关引理

引理1[3]若正整数n=p1r1，p2r2，…，pkrk，其中p1,p2,…pk为素数，则欧拉函数

Smarandache函数

S(n)=max{S(p1r1),S(p2r2)，…S(pkrk)}。

引理2[3]对于整数k与素数p，有S(Pk)≤kp；若进一步有k

引理3[3]当n≥2时，有φ(n)

2 主要结果

定理广义欧拉函数方程

φ2(n)=S(n28),n≥2

(2)

的正整数解为n=12769，25538。

证明当n=2时，φ2(2)=1,S(228)=32，显然φ2(2)≠S(228)，于是n=2不是方程(2)的解。

当n≥3时，设n=p1r1，p2r2，…，pkrk，其中p1,p2…pk为素数，由引理1，

S(n28)=S(p128r1p228r2…pk28rk)=

max{S(p128r1),S(p228r2)，…S(pk28rk)}=

S(p28r)，

(3)

其中p为n的素因数，r为素因数p在n中的次数。又

(4)

若(3)，(4)式均成立，即得(2)式有解。

下面就p，r的不同取值分17种情况分别加以讨论：

情形1 当p=2时：

(1)若r=1时，则(4)式为φ(m)=2S(228)=64,m=85，128，136，160，170，192。又(m,p)=1，则m=85，n=pr·m=170。将其代入(3)式S(17028)=459≠32，此时n=170不是(2)式的解。

(2)若r=2时，则(4)式为φ(m)=S(256)=60，m=61，77，93，99，122，124，154，183，186，198。又(m,p)=1，则m=61，77，93，99，183，n=pr·m=244，308，372，396，732。将其代入(3)式，可得

S(24428)=S(73228)=1708≠60，

S(30828)=S(39628)=297≠60，

S(37228)=868≠60，

故n=244，308，372，396，732不是(2)式的解。

(3)若r=3时，则(4)式为2φ(m)=S(284)=88，φ(m)=44，m=69，92，138。又(m,p)=1，则m=69，n=pr·m=552。将其代入(3)式S(55228)=621≠88，此时n=552不是(2)式的解。

(4)若r=4时，则(4)式为4φ(m)=S(2112)=116，φ(m)=29，由引理2可知，此时(2)式无解。

(5)若r=5时，则(4)式为8φ(m)=S(2140)=144，φ(m)=18,m=19，27，38，54。又(m,p)=1，则m=19，27，n=pr·m=608，864。将其代入(3)式得S(60828)=513≠144与S(86428)=60≠144，此时n=608，864不是(2)式的解。

(6)若r=6时，则(4)式为16φ(m)=S(2168)=172，φ(m)不是整数，故(2)式无解。

(7)若r=7时，则(4)式为32φ(m)=S(2196)=200，φ(m)不是整数，故(2)式无解。

(8)若r=8时，则(4)式为64φ(m)=S(2224)=228，φ(m)不是整数，故(2)式无解。

(9)若r=9时，则(4)式为128φ(m)=S(2252)=256，得φ(m)=2，则m=3，4，6。又(m,p)=1，则m=3，n=pr·m=1536。将其代入(3)式得

S(153628)=60≠256，

此时n=1536不是(2)式的解。

(10)若r=10时，则(4)式为256φ(m)=

S(2280)=284,φ(m)不是整数，故(2)式无解。

(11)若r=11时，则(4)式为512φ(m)=

S(2308)=312，φ(m)不是整数，故(2)式无解。

(12)若r≥12时，则56r≥S(228r)=2r-2φ(m)≥2r-2不成立，此时(2)式无解。

情形2 当p=3时：

(1)若r=1时，则(4)式为φ(m)=S(328)=60,m=61，77，93，99，122，124，154，183，186，198。又(m,p)=1，则m=61，77，122，154，n=pr·m=183，231，366，462。将其分别代入(3)式，可得

S(18328)=S(36628)=1708≠60，

S(23128)=S(46228)=297≠60，

此时n=183，231，366，462不是(2)式的解。

(2)若r=2时，则(4)式为3φ(m)=S(356)=117,φ(m)=39，由引理2可知，此时(2)式无解。

(3)若r=3时，则(4)式为9φ(m)=S(384)=171,φ(m)=19，由引理2可知，此时(2)式无解。

(4)若r=4时，则(4)式为27φ(m)=S(3112)=231,φ(m)不是整数，故(2)式无解。

(5)若r=5时，则(4)式为81φ(m)=S(3140)=285,φ(m)不是整数，故(2)式无解。

(6)若r=6时，则(4)式为243φ(m)=S(3168)=342，φ(m)不是整数，故(2)式无解。

(7)若r≥7时，则84r≥S(328r)=3r-1φ(m)≥3r-1不成立，此时(2)式无解。

情形3 当p=5时：

(1)若r=1时，则(4)式为2φ(m)=S(528)=120,φ(m)=60,则m=61，77，93，99，122，124，154，183，186，198。又(m,p)=1，则m=61，77，93，99，122，124，154，183，186，198，此时有n=pr·m=305，385，465，610，620，770，915，930，990。将其分别代入(3)式，可得

S(30528)=S(61028)=S(91528)=1708≠120，

S(46528)=S(62028)=S(93028)=868≠120，

S(38528)=S(49528)=S(77028)=S(99028)=

297≠120，

此时n=305，385，465，610，620，以及770，915，930，990都不是(2)式的解。

(2)若r=2时，则(4)式为10φ(m)=S(556)=230，φ(m)=23，由引理(2)可知，此时(2)式无解。

(3)若r=3时，则(4)式为50φ(m)=S(584)=345,φ(m)不是整数，故(2)式无解。

(4)若r=4时，则(4)式为250φ(m)=S(5112)=455,φ(m)不是整数，故(2)式无解。

(5)若r≥5时，则

140r≥S(528r)=2·5r-1φ(m)≥2·5r-1不成立，此时(2)式无解。

情形4 当p=7时：

(1)若r=1时，则(4)式为3φ(m)=S(728)=175,φ(m)不是整数，故(2)式无解。

(2)若r=2时，则(4)式为21φ(m)=S(756)=343，φ(m)不是整数，故(2)式无解。

(3)若r=3时，则(4)式为147φ(m)=S(784)=511,φ(m)不是整数，故(2)式无解。

(4)若r≥4时，则

196r≥S(728r)=3·7r-1φ(m)≥3·7r-1不成立，此时(2)式无解。

情形5 当p=11时：

(1)若r=1时，则(4)式为5φ(m)=S(1128)=286,φ(m)不是整数，故(2)式无解。

(2)若r=2时，则(4)式为55φ(m)=S(1156)=572，φ(m)不是整数，故(2)式无解。

(3)若r=3时，则(4)式为605φ(m)=S(1184)=847，φ(m)不是整数，故(2)式无解。

(4)若r≥4时，则

308r≥S(1128r)=5·11r-1φ(m)≥5·11r-1不成立，故(2)式无解。

情形6 当p=13时：

(1)若r=1时，则(4)式为6φ(m)=S(1328)=338,φ(m)不是整数，故(2)式无解。

(2)若时，则(4)式为78φ(m)=S(1356)=676,φ(m)不是整数，故(2)式无解。

(3)若时，则(4)式为1014φ(m)=S(1384)=1014,φ(m)=1,则m=1,2，又(m,p)=1，则m=1，2，n=pr·m=2197，4394。将其分别代入(3)式，可得S(219728)=S(439428)=338≠1014，此时n=2197，4394不是(2)式的解。

(4)若r≥4时，则

364r≥S(1328r)=6·13r-1φ(m)≥6·13r-1不成立，此时(2)式无解。

情形7 当p=17时：

(1)若r=1时，则(4)式为8φ(m)=S(1728)=459，φ(m)不是整数，故(2)式无解。

(2)若r=2时，则(4)式为136φ(m)=S(1756)=901,φ(m)不是整数，故(2)式无解。

(3)若r≥3时，则

476r≥S(1728r)=8·17r-1φ(m)≥8·17r-1不成立，故(2)式无解。

情形8 当p=19时：

(1)若r=1时，则(4)式为9φ(m)=S(1928)=513,φ(m)=57，由引理2可知，此时(2)式无解。

(2)若r=2时，则(4)式为171φ(m)=S(1956)=1026,φ(m)=6，则m=7，9，14，18。又(m,p)=1，则m=7，9，14，18，n=pr·m=2527，3249，5054，6498。将其分别代入(3)式，可得

S(252728)=S(324928)=S(505428)=

S(649828)=513≠1026，

此时n=2527，3249以及5054，6498不是(2)式的解。

(3)若r≥3时，则

532r≥S(1928r)=9·19r-1φ(m)≥9·19r-1不成立，此时(2)式无解。

情形9 当p=23时：

(1)若r=1时，则(4)式为11φ(m)=S(2328)=621,φ(m)不是整数，故(2)式无解。

(2)若r=2时，则(4)式为253φ(m)=S(2356)=1242,φ(m)不是整数，故(2)式无解。

(3)若r≥3时，则

644r≥S(2328r)=11·23r-1φ(m)≥11·23r-1不成立，故(2)式无解。

情形10 当p=29时：

(1)若r=1时，则(4)式为14φ(m)=S(2928)=812，φ(m)=58，则m=59，118。又(m,p)=1，则m=59，118，n=pr·m=1711,3422。将其分别代入(3)式，可得S(171128)=S(342228)=1652≠812，此时n=1711，3422不是(2)式的解。

(2)若r=2时，则(4)式为406φ(m)=S(2956)=1595,φ(m)不是整数，故(2)式无解。

(3)若r≥3时，则

812r≥S(2928r)=14·29r-1φ(m)≥14·29r-1不成立，故(2)式无解。

情形11 当p=31时：

(1)若r=1时，则(4)式为15φ(m)=S(3128)=868,φ(m)不是整数，故(2)式无解。

(2)若r=2时，则(4)式为465φ(m)=S(3156)=1705,φ(m)不是整数，故(2)式无解。

(3)若r≥3时，则

868r≥S(3128r)=15·31r-1φ(m)≥15·31r-1不成立，故(2)式无解。

情形12 当p=37时：

(1)若r=1时，则(4)式为18φ(m)=S(3728)=1036,φ(m)不是整数，故(2)式无解。

(2)若r=2时，则(4)式为666φ(m)=S(3756)=2035，φ(m)不是整数，故(2)式无解。

(3)若r≥3时，则

1036r≥S(3728r)=18·37r-1φ(m)≥18·37r-1不成立，故(2)式无解。

情形13 当p=41时：

(1)若r=1时，则(4)式为20φ(m)=S(4128)=1148，φ(m)不是整数，故(2)式无解。

(2)若r=2时，则(4)式820φ(m)=S(4156)=2255,φ(m)为不是整数，故(2)式无解。

(3)若r≥3时，则

1148r≥S(4128r)=20·41r-1φ(m)≥20·41r-1不成立，故(2)式无解。

情形14 当p=43时：

(1)若r=1时，则(4)式为21φ(m)=S(4328)=1204，φ(m)不是整数，故(2)式无解。

(2)若r=2时，则(4)式为903φ(m)=S(4356)=2365,φ(m)不是整数，故(2)式无解。

(3)若r≥3时，则

1204r≥S(4328r)=21·43r-1φ(m)≥21·43r-1不成立，故(2)式无解。

情形15 当p=47时：

(1)若r=1时，则(4)式为23φ(m)=S(4728)=1316,φ(m)不是整数，故(2)式无解。

(2)若r=2时，则(4)式为1081φ(m)=

S(4756)=2585，φ(m)不是整数，故(2)式无解。

(3)若r≥3时，则

1316r≥S(4728r)=23·47r-1φ(m)≥23·47r-1不成立，故(2)式无解。

情形16 当p=53时：

(1)若r=1时，则(4)式为26φ(m)=S(5328)=1484,φ(m)不是整数，故(2)式无解。

(2)若r=2时，则(4)式为1378φ(m)=

S(5356)=2915,φ(m)不是整数，故(2)式无解。

(3)若r≥3时，则

1484r≥S(5328r)=26·53r-1φ(m)≥26·53r-1不成立，故式无解。

情形17 当p≥57时：

S(p28)=28p,即(p-1)φ(m)=56p。又(p-1,p)=1，所以(p-1)|56与p≥57矛盾，所以此时(2)式无解。

S(p56)=56p，即(p-1)φ(m)=112。又因为p≥57，可得p=113，φ(m)=1，m=1，2，n=pr·m=12769，25538。将其分别代入(3)式，可得

S(1276928)=S(2553828)=6328=S(11356)，

此时n=12769，25538是(2)式的解。

(3)若r≥3时，则

即56r≥(p-1)pr-2，

而p-1≥56，pr-2>r，

所以56r≥(p-1)pr-2显然不成立，所以此时(2)式无解。

终上所述，可得广义欧拉函数方程φ2(n)=S(n28),n≥2的正整数解为n=12769，25538。证毕。