论体重分布Markov skeleton process的应用 ①
鲁 禹, 周 波
(佳木斯大学理学院,黑龙江 佳木斯 154007)
0 引 言
肥胖症在世界各国越来越受到关注。源于世界卫生组织数据显示,约有340万人每年因肥胖死亡(主要由于引发的各种疾病)。根据英国医学杂志《柳叶刀》的报道中国平均肥胖率达到12%,肥胖人口规模超2.5亿,肥胖总人数高居世界第一。截止至2020年第一季度我国网民自身体重超重比占达36%。当今减肥市场鱼龙混杂,不乏无良商家,因此更加需要系统,科学的减肥方法帮助肥胖人群健康的减肥。运用“减肥计划模型”[1],通过能量平衡原理:体重在某一时段内发生变化的数值与人体内能量变化数值相等,利用该阶段内摄入热量数值与消耗热量数值的差值,建立差分方程,表示这一时段内关于人体重的函数。“减肥计划模型”将体重仅仅看成是时间的函数,忽略不同人的身体情况(如年龄,性别,健康状况等);同时此模型无法表示出体重的瞬时分布。1997年,侯振挺教授等人首次提出马尔可夫骨架过程(Markov skeleton process),并利用其理论合理应用于排队论、控制论等领域,解决了排队论的瞬时分布、平稳分布、遍历性等一系列经典难题。将减肥体重分布模型作为是随机环境流体模型的推广,借助马尔可夫骨架过程将人类体重视作一类较为综合随机过程,进一步考虑了不同人群之间的差异;同时对任一时刻的体重分布做出表述。
1 模型描述
利用马尔可夫骨架过程及其极限分布考虑减肥过程中的的体重分布模型,根据相关生理特点,做出如下假设:
(2)人在不同的代谢状态下有着不同的能量摄入速度,V1,V2,…,VN,(例如在夏季和冬季人体的能量摄入速度就是不同的),能量摄入速度是被一个在有限状态集E={1,2,…,N}中取值的半马尔可夫过程{X(t);t≥0}所控制,在t时刻人体的摄入速度为VX(t);

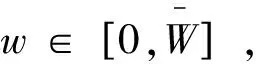
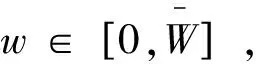
令

2 体重瞬时分布过程的数学建模
令θ(t)=inf{s≥0,X(t-s)≠X(t)}
θ(t)表示时刻t以前X(·)的最后一个断点到t的时间间隔。


以T1表示X(t)在时刻0以后的第一个跳跃时刻,令


Fi,k(t)=


于是有:
考察W(t)的极限状态,令
G(t)=(W(t),X(t),θ(t)),t>0;
以(EG,I)表示G(t)的状态空间。假定P(W=0)=1(其直观意义是体重可以以概率1减少)。
并设{G(t),t≥0}是即约的,正常返的。取定i0∈E,这里i0表示W(t)=0,θ(t)=0时,X(t)所在状态,令
r1=inf{t>0|G(t)=(0,i0,0)},r0≡0,
rn+1=rn+θrnrn,n=1,2,…

∀x∈EG,t≥0,
令


易验证{G(t),t≥0}是以{rn}为骨架时序列的正常返的Doob骨架过程。且设X(t)在各状态的逗留时间的分布函数是绝对连续的随机变量,则可知D(x,·)是绝对连续的(∀x∈EG),则{G(t),t≥0}是严正规的马尔可夫骨架,得G(t)的极限分布P(·)如下:

A=W×E×{0,1}×R+×R+能确定{W(t),t≥0}的极限分布。



∀i,j∈E,w,θ∈IR+,W,B∈B(IR+),
令


=
P(W(t)∈W,X(t)=j,θ(t)∈
B,t 显然有 (1-Fi,θ(t))I[0,S(w,i)](t)δijIB(t+θ) 由骨架过程的向后方程理论(参考[2])可得: S(w,i),W,j,B,t-s(w,i))+ θ+s,W,j,B,t-s) 通过定理 1,可以唯一确定体重分布过程的有限维分布。 注意: P(G(t)∈A,t 这里A=W×{j}×B,x=(w,i,θ) 马尔可夫骨架过程属综合随机过程,涵盖面较广,进而其应用前景十分宽广,目前侯振挺等已在多个领域运用马尔可夫骨架过程理论体系均获得成功。马氏骨架过程理论研究最新成果显示,通过进一步探讨马尔可夫骨架过程的理论,对一类特殊的马尔可夫骨架过程-Doob骨架过程并建立若干状态下骨架过程,并应用于马尔可夫骨架过程的瞬时性态理论,获得了体重分布模型的主要参量过程瞬时分布,便于减肥人群掌握各个时刻的体重情况。同时利用随机流体模型可精准衡量并记录能量数值变化。 体重分布模型具有一定代表性,可适用于较多领域,其证明思路完全类似。尤其在经济方面可解决较多问题,如银行存贷差,保险公司盈利等。
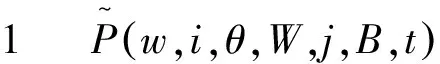
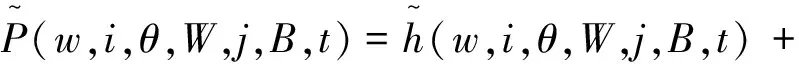
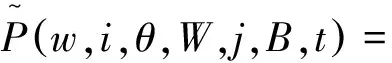
3 结 语

