电动执行机构碟簧组件的设计与研究 ①

纪慧泉， 张剑峰

(1.江苏旅游职业学院，江苏 扬州 225000;2.扬州大学机械工程学院，江苏 扬州 225127)

0 引 言

碟形弹簧简称碟簧，它作为一种重要的弹性承载元件，具有体积小、承载能力大、缓冲和减震能力强等特点[1]。碟簧具有变刚度特性，采用不同的组合方式可以得到不同的力学性能[2-3]。它的优点是在很小的变形条件下,能承受较大载荷,从而减小整机的体积和重量,节省空间和原材料，因此被广泛用于钻机、模具、阀门驱动装置等要求体积小受力大的装置上[4-5]。

阀门驱动装置也称为电动执行机构，它通常采用力矩控制方式来控制阀门的开、关或执行相应的阀位指令[6]，其中采用碟簧组件的力矩控制机构具有体积小、承载大、可靠性高等优点，被广泛应用于电动执行机构。最近几年，国内外学者利用数值法对碟簧进行了广泛的研究。Ozaki等利用数值法系统研究了静态摩擦边界对碟簧静态和动态行为的影响[7]。Curti，P.Bagavathiperumal等应用有限元方法对碟形弹簧在轴向载荷下的载荷-变形特性进行了预测[8-9]。Patangtalo等利用数值法研究了复合碟簧的载荷-位移特性曲线[10-11]。Fawazi等利用数值法对具有特定载荷-位移特性曲线的开槽碟簧的几何参数进行了优化设计，而后又利用数值法预测了其悬臂片簧部分的弯曲度对碟簧载荷-位移特性曲线的影响[12-13]。廖日东等利用数值法计算了某非标碟簧在平稳压缩和释放过程中该碟簧的应力及变形，给出了加载-卸载刚度曲线[14]。Erochko等为了增强自复位耗能( self-centering energy dissipation, SCED) 支承的变形能力和承载能力，提出了基于组合碟簧的SCED支承结构[15]。XU Longhe等对SCED支承的组合碟簧力学性能进行了研究，得到“旗形”滞回曲线[16]。

以上研究利用数值模拟方法对碟簧的各种性能进行了分析，但大部分并未结合试验、理论计算数据进行比对，得出的结论具有一定的价值，但同时也存在一定的局限性。本文以传统力学为基础，建立电动执行机构碟簧组件的力学模型，得到初步的力学参数；依托有限元得到碟簧直观的变形-受力数据，用试验方法得到碟簧真实的变形—受力数据。分析对比三者数据，为电动执行机构碟簧组件可靠、快速、智能化设计提供参考。

1 电动执行机构结构及力矩控制机构

电动执行机构主要包括电机、箱体、蜗轮蜗杆主传动机构、力矩控制机构、碟簧组件、行程控制机构、手切换等部分，其结构如图1所示。

图1 电动执行机构结构图

2 碟簧组件变形-受力分析

2.1 电动执行机构蜗杆碟簧组件

碟簧根据厚度分为无支撑面碟簧和有支撑面碟簧[17]。电动执行机构一般采用如图2所示的无支撑面碟簧，通常采用如图3所示的n个同方向同规格碟簧进行对合组合。

图2 碟簧结构简图

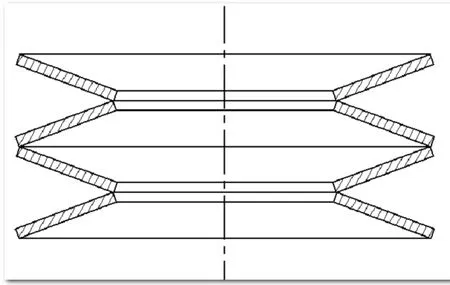
图3 对合组合碟簧

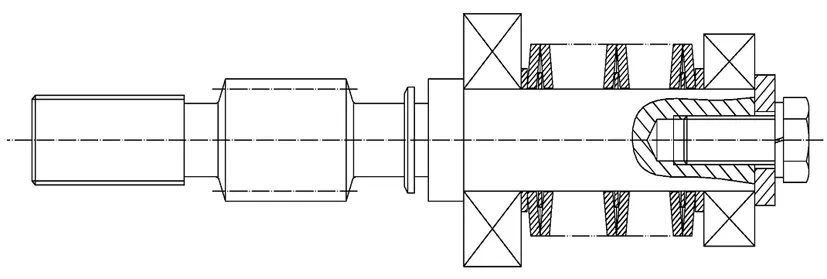
图4 碟簧组件

表1 碟簧参数

2.2 碟簧变形-受力理论分析计算

国际上采用Alem-Laszb公式计算无支撑面碟簧的变形-受力，简称为A-L解，计算公式为：

(1)

式中：F为载荷，E为弹性模量，D为碟簧外径，μ为泊松比，h0为碟簧最大压缩量，t为碟簧厚度，f为变形量，采用无支撑面碟簧时，K4=1。其中计算系数K1按(2)计算。

(2)

式中：C=D/d

根据Alem-Laszb计算公式，利用maltab软件编制单片碟簧的变形—受力函数。变形量从0开始，以0.05mm增量计算碟簧受力随变形的函数关系，直至变形量f=0.75h0时停止计算。将数据拟合成如图5所示的变形—受力曲线。根据曲线知，当单片碟簧变形量fL0=0.75h0(1.35mm)时，碟簧受力F0=12530N；当碟簧变形量fL1=1.15mm时，碟簧受力F=11050N，恰好等于1.3F,即F1.3max。

本文通过利用自适应神经模糊推理系统(ANFIS)实现基于回跳电压的锂离子电池SOC预测模型的建立。ANFIS的学习算法过程和架构实际上综合了许多种有监督学习功能的前馈神经网络的学习方法。自适应网络就是一个由多节点以及连接它们的网络组成的网络结构,更进一步,部分或者所有节点具有自适应性,这意味着它们的输出取决于这些节点的激励函数的参数(一个或多个),同时学习规则规定了这些参数该如何改变以使规定的误差降到最小。自适应网络的基本学习规则是基于梯度下降和链式法则[7],梯度法由于它的缓慢以及容易陷入局部收敛,因此ANFIS采用混合学习规则,混合学习方法能够加速学习进程。

图5 碟簧matlab理论计算值

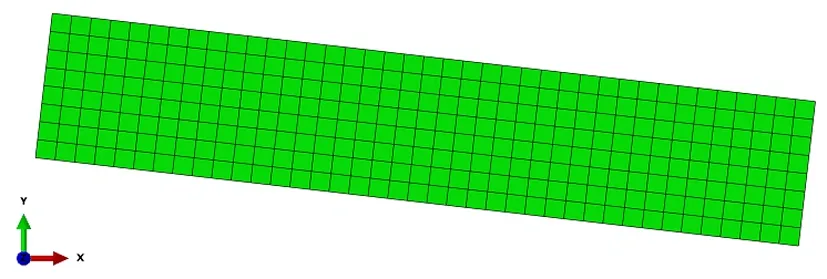
图6 碟簧有限元二维简化模型

2.3 碟簧有限元分析

不计摩擦力时，对合碟簧组件受力Fz=F，即每片碟簧受力相同。总变形量fz=i·f，i为碟簧片数，f为单片变形量。因此只需对一片或者几片碟簧进行模拟分析，然后根据碟簧片数进行相关换算即可。

2.3.1 加载及边界条件设置

碟簧结构、边界和载荷条件都呈轴对称分布，因此在abaqus有限元软件中选用轴对称模型进行建模，建立如图6所示的二维对称模型。对模型施加与Y轴的对称约束，碟簧底部位移约束施加在外径D的外端面(即图2中的B面)，这样既可以模拟真实的载荷、边界条件，又可以节省计算资源，还能得到很高的精确。在后处理过程中，为得到较为直观的结果，可将二维模型沿对称轴旋转360度，得到如图7所示的三维图。

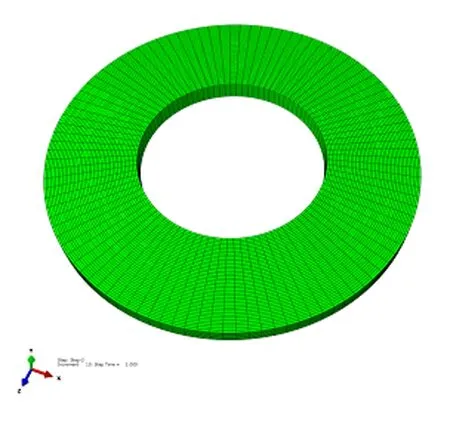
图7 碟簧有限元三维模型

图8 碟簧abaqus有限元模拟值

2.3.2 有限元力学分析数据

给碟簧内径d的外端面(即图2中的A面)一周施加沿Y轴负方向f=1.35mm(此时理论变形量f=0.75h0)的位移载荷，模拟碟簧变形-受力关系，提取从0到1.35mm范围内碟簧变形—受力数据并将其绘制成如图8所示的变形-受力曲线，从图知当f=0.75h0，有限元分析得到的载荷为13110N。

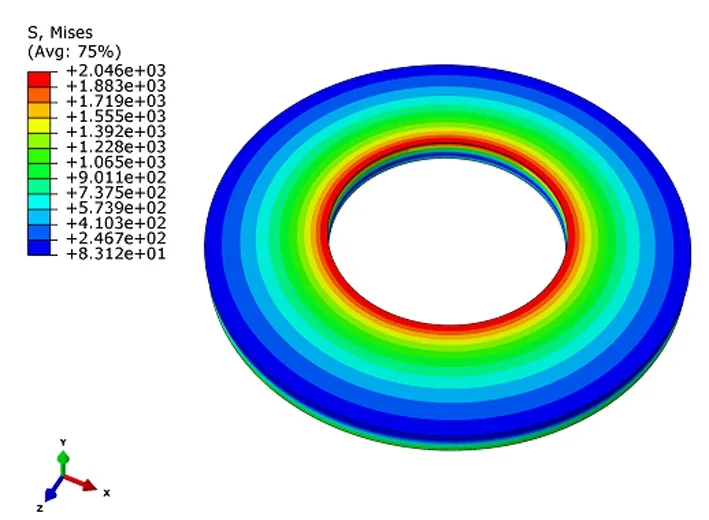
图9 碟簧应力云图

图10 带测试工装的碟簧组件

提取F=13110N(即f=0.75h0)时的数据，得到图9所示的应力云图。根据图知，最大应力位置处在碟簧的A面，与实际情况一致，最大应力σI=2.046e3=2046MPa，未超出碟簧许用应力范围(GB/T1972的规定，静载荷作用下，蝶簧的许用应力以σI(图2中A面)为准，计算得到的σI在变形f=0.75h0时，不得超过240kgf/mm，即2400MPa)。

2.3.3 碟簧组件压缩试验

选取16片碟簧对合，与工装一起组装成如图10所示的碟簧组件作为压缩试验对象，利用图11～12所示的碟簧压缩试验机对其进行压缩变形测试。

图11 碟簧压缩试验机

图12 碟簧压缩试验细节

采用变形-负载模式，单片最大变形量fs1=0.75h0(总位移fz=i·f=16×1.35=21.6mm)给碟簧组件进行加载，加载速度为1mm/s。得到如图13所示的变形-受力曲线。提取数据，变形量fs1=0.75h0对应的负载Fs1=13658.6N。

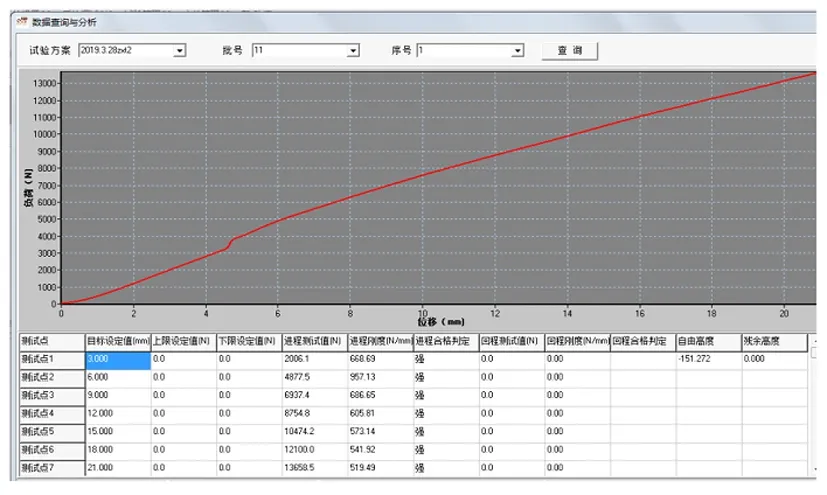
图13 碟簧组件压缩试验数据

2.3.4 数据对比及误差分析

将理论计算、有限元分析、压缩试验得到的变形-受力数据用matlab软件拟合成如图14所示的变形-受力曲线对比图。

图14 碟簧数据对比图

对比曲线知，有限元曲线大部分处在理论计算和试验曲线之间,且处在理论曲线的上部；变形量f越大，有限元曲线与试验曲线越接近，偏差值越小。理论计算与试验曲线的偏差与其对比，偏差较大(偏差在碟簧设计误差范围内)。提取变形f=0.7h0时对应的理论计算、有限元、试验受力数值，以试验数据为整定基准值，按公式(3)求出理论计算、有限元分析与其对比的误差率，具体见表二。

(3)

式中：δ0为误差率，%；Fm为变形量为0.7h0时，碟簧受力理论计算、有限元计算值，N；Fs为变形量为0.7h0时，碟簧受力试验值,N。

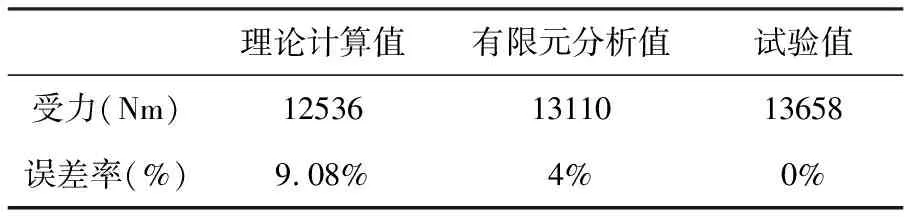
表2 单片碟簧受力值及误差率(f=0.75h0时)

分析图14中的曲线及误差率，出现该情况的原因主要有以下几点：

1) Alem-Laszb计算方法存在一定的局限性,此方法假定碟簧的矩形剖面不变，未考虑碟簧受力变形的情况，无法对公式中的参数进行修正，只能给出碟簧受力—变形的近似解。

2) 变形量f增大，碟簧受力杠杆臂变小，实际负荷比理论值大，有限元法可对碟簧受力变形后的形状和摩擦力进行模拟计算，更接近实际工况，因此在碟簧的变形—受力曲线对比图中，有限元和试验曲线大部分都在理论曲线上部。

3)abaqus有限元求解器在迭代计算时，可对维数巨大的节点刚度矩阵进行迭代计算，根据迭代结果不断修正矩阵方程进行下一步的迭代计算，计算结果与试验数据更加吻合。

3 结 语

1)碟簧作为电动执行机构转矩控制信息采集的源头，其可靠性设计十分重要。传统力学方法作为机械设计重要组成部分，依旧发挥着重要作用，为产品初期整体方案排布、论证提供着重要理论依据和支撑。

2)有限元作为一种现代化的设计方法，具有成本低、周期短的等优势，可快速计算、模拟出诸如碟簧等机械产品的各项性能指标，计算准确度较高，具有很高的参考价值。

3)试验是检验机械产品性能的重要手段，针对一些重要零件，一般需要试制零件并采购相关试验设备进行试验验证。这需耗费一定的时间和经济成本，对产品的研发进度造成一定的影响，在时间上具有一定的滞后性。

4)将传统力学、有限元、试验方法相结合，既可提高电动执行机构碟簧组件设计的可靠性，又可缩短整个产品研发周期，是一种较为理想、科学的机械设计方法。