一种数据流自适应两阶段聚类算法

李志杰 廖旭红 刘基旺 江华

摘  要：K-means是最常用的批量聚类方法，然而该算法需要多次迭代并不能直接用于数据流聚类。文章基于自适应谐振理论（ART），提出一种针对数据流聚类的自适应两阶段聚类算法（ATPC）。该算法分为在线自适应微聚类和离线全局批量聚类两个阶段，自适应生成微簇，具有线性计算复杂度。在MOA平台上真实与模拟数据流的实验结果验证了ATPC方法的高效性。

关键词：数据流;聚类;两阶段;自适应谐振理论;微簇

中图分类号：TP311.13 文献标识码：A文章编号：2096-4706（2021）14-0124-03

Abstract： K-means is the most commonly used batch clustering method， however， this algorithm requires several iterations and cannot be directly used for data stream clustering. In this paper， we propose an adaptive algorithm with two phases for data stream clustering （ATPC） based on adaptive resonance theory （ART）. ATPC is divided into two phases， online adaptive microclustering and offline global batch clustering， and adaptively generates microclusters with linear computational complexity. Experimental results on the real dataset and simulated data streams validate the efficiency of ATPC method.

Keywords： data stream; clustering; two phases; adaptive resonance theory; micro cluster

0  引  言

社交網络、移动通信、物联网等众多快速发展的产生数据流场景，迫切需要满足数据流特征的实时聚类技术[1-3]。数据流本质上可视为只能读取一次的数据序列。设计数据流聚类算法，必须满足如下数据流公理[4，5]：

（1）每个数据项只能被观察和处理一次。

（2）处理每个数据项只能消耗较少的时间。

（3）只能存储一小部分数据项，其内存占用与数据流长度成亚线性（sublinear）关系。

（4）必须做到随时提供算法的解答。

（5）能够有效检测与处理数据流的概念漂移。

K-means算法是离线聚类的基础方法之一[6]。该算法需要在数据集上迭代优化，并且还要预先指定簇的个数。然而，由聚类创建的簇的数量在学习开始之前是未知的，例如细分营销客户群体、社交网络中寻找社区等。因此，K-means无法直接用于数据流聚类。

与K-means方法不同，自适应谐振理论（adaptive resonance theory， ART）可以实现样本数据新建模式类的自适应。聚类过程中，当输入样本与当前某一模式类高度相似时则将其归为这一模式类，而当所有模式类的相似度都不超过警戒门限时，则新建模式类来存储当前输入模式，自动增加聚类簇的个数[7，8]。

基于ART理论，数据流聚类在线阶段可以实现自适应微聚类;然后，我们以保存在线阶段统计数据的微簇（microcluster）为伪点，数据流聚类的离线阶段进一步消除噪音并全局聚类。

1  相关工作

1.1  K-means算法

K-means算法计算数据点彼此之间的距离，依靠相似性进行分组。K-均值算法是一种无监督的迭代优化学习算法，将一个给定的数据集分类为K个聚类。算法不断进行迭代计算和调整，直到达到一个理想的结果。K-means算法的伪代码为：

1 初始化：样本数n， 聚类数K，

原始聚类中心u1，…，uk;

2  do 按照最近邻ui （i=1，…，k）分类n个样本;

3     重新计算聚类中心u1，…，uk;

4  until u1，…，uk不再改变;

5  return u1，…，uk.

K-means算法中“K”的选取是人为选定的，需要事先指定划分的簇的个数。绝大部分的实际运用中，我们是无法提前预知数据样本簇的个数，导致K-means算法的结果可能不符合真实情况。

K-Means本质上是一种传统的离线聚类算法，它需要反复对数据集进行迭代，不断调整质心位置直到质心趋于稳定[6]。而由于数据流的连续性和无穷性，导致几乎不可能将数据样本存储下来并反复迭代，故无法对数据流使用K-Means算法来完成聚类。

1.2  数据流sketch数据结构

数据流聚类问题的解决方案都使用了数据流sketch的概念。一个sketch是一个数据结构，自带算法读取数据流并存储足够的信息，以便能够回答一个或多个关于数据流的查询要求[9]。我们将sketch视为更高级别数据流学习和挖掘算法的基本组成部分。由于这些算法会创建许多sketch用于同时跟踪不同的统计数据，因此要求sketch只能使用少量的内存。

一个sketch算法主要包含三个操作：

（1）Init（...）操作：初始化数据结构，可能有一些参数，如要使用的内存量。

（2）Update（项）操作，将应用于流上的每个数据项。

（3）Query（...）操作：返回到目前为止读取的数据流上感兴趣的函数的当前值（也可能没有参数）。

1.3  自适应谐振理论ART

神经网络中自适应谐振理论ART可以实现对样本数据自适应的新建模式类[10]。一般来说，ART模型由输入层（F1）和识别层（F2）组成，如图1所示。自适应谐振的运行过程主要分为四个阶段：识别阶段、比较阶段、搜索阶段和学习阶段。

训练过程中，当输入样本与当前神经网络中某一模式类高度相似时自动将其归为这一模式类;当所有模式类的相似度都不超过警戒门限即无法匹配当前网络中任意一模式类时，则新建模式类来存储当前输入模式，从而实现对数据流的聚类且自动增加聚类簇的个数，在提高数据流聚类性能的同时，也弥补了K-means算法预定簇类的缺陷。

2  自适应两阶段数据流聚类方法

基于sketch概念和ART机制，本文设计的数据流的聚类算法分为在线与离线两个阶段。

2.1  在线阶段

考虑一个数据流x（1），x（2），...，x（n），...，每个实例包含d个特征，x（n）=∈Rd。在任何时候到达的实例，都进入到微簇中，过程如下：

（1）首先读入第一条实例，构造包含一个实例的微簇。

（2）陆续接收第2条实例、第3条实例…。每个实例到达时，计算该实例与目前所有微簇特征向量的距离，实例加入距离最近的微簇。

（3）实例加入距离最近的微簇后，如果此时的簇直径已经大于T，则新建一个包含该实例的微簇。

微簇是旨在压缩进入到其中的数据流实例的一种sketch结构，本文定义微簇为：

定义1：微簇（micro cluster， MC）。微簇是微聚类的一种压缩结构，用于表示聚类特征树叶子节点中实例的统计信息，MC=（n，LS，SS，T，L）。其中，

标量n：到目前为止的实例数量;

向量LS=，到目前为止的实例之和;

向量SS，到目前为止的实例的平方和，其中

SSj=;

T：微簇直径;

L：孩子节点数量阈值。

根据微簇定义，可以很容易计算微簇中心向量=LS/n。同时，向现有MC添加实例和合并两个现有MC的操作也是非常直接和简单的。

2.2  离线阶段

离线阶段使用在线阶段形成的sketch，以有规律的时间间隔或者按需高效地计算全局最终的聚类。

本文的离线阶段主要由两个过程组成。首先，积极检测不属于真实聚类的随机数据，消除噪音。把目前所有的MC根据其大小按降序排序，得到一个正的分布。然后，噪声将出现在右下尾部，我们首先通过切割后45%的点来消除这个尾巴。

当微簇实例数量分布的尾巴消失后，离线阶段再以剩余的微簇为伪点，采用传统的K-means方法按需高效计算最终聚类。

自适应两阶段数据流聚类方法符合数据流聚类的全部要求。

3  实验结果与分析

Massive Online Analysis（MOA）是数据流分析主流平台，本文实验使用MOA生成的人工数据流、以及真实數据集对算法的性能进行评价和比较。实验在2.60 GHz、Intel（R） Core（TM） i7-6700HQ CPU、内存16 GB、操作系统Windows 10的计算机上进行。

3.1  数据集

3.1.1  人工数据集

本文的人工数据集使用MOA数据流生成器RandomRBFGeneratorEvents，该生成器生成的数据点依据所选范围具有类标签，以及反映数据点年龄的权重。所有聚类类别都具有同样期望的数据点数量。

RandomRBFGeneratorEvents数据流生成器包含的参数有：

在数据空间中移动的聚类数量;

生成数据点的数量;

移动时间间隔;

聚类半径;

维度;

噪声率。

3.1.2  真实数据集

kddcup.data_10_percent是KDD Cup 1999竞赛项目10%的训练数据集，共有494 021个样本，用于预测网络连接是“异常”连接类型或“正常”连接类型。本文预处理该数据集后，形成kddcup.data_10_percent_corrected.arff文件，用于真实数据集聚类分析。

kddcup.data数据集的每个样本包含41个条件属性，一个类别属性。42个属性中，33个是连续的数字类型，其余9个属性是离散类型，即标称型属性。

3.2  实验结果与分析

实验采用聚类映射度量（Cluster Mapping Measure， CMM）、纯度（Purity， P）、剪影系数（Silhouette Coefficient， SC）三种性能指标评估聚类性能。比较方法有ATPC

（adaptive two phases algorithm for data stream clustering）、clustream、denstream和ClusTree等。

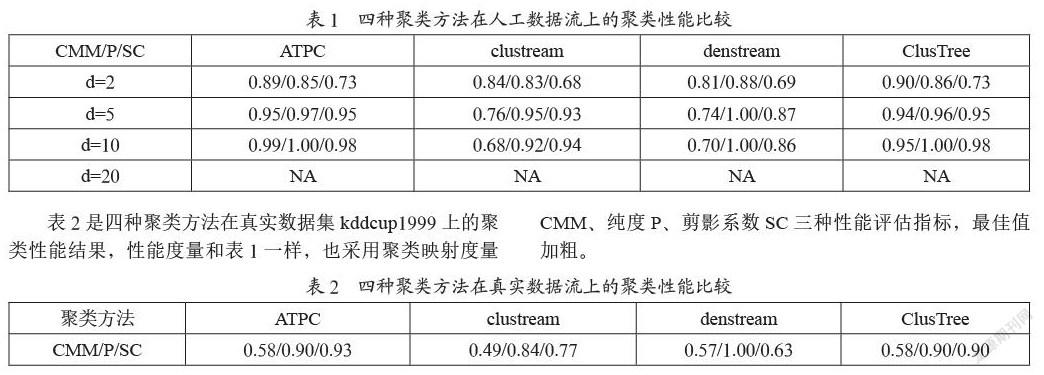
表1是四种聚类方法在人工数据流上的聚类实验结果。RandomRBFGeneratorEvents数据流样本数量为50 000，样本维度（dimensionality）分别取2、5、10、20，各场景的性能最佳值用加粗标示，NA表示MOA内存溢出。

表2是四种聚类方法在真实数据集kddcup1999上的聚类性能结果，性能度量和表1一样，也采用聚类映射度量CMM、纯度P、剪影系数SC三种性能评估指标，最佳值加粗。

从表1和表2的实验结果，我们不难看出：无论是人工数据流，还是真实数据集，本文提出的ATPC聚类方法，在大部分的场景下，其综合聚类性能优于其他流行的方法。

4  结  论

数据流聚类通常采用两阶段聚类。本文基于自适应谐振理论ART，在线阶段自适应微聚类，微簇个数自动生成。离线阶段先消除噪声再全局聚类，具有线性计算复杂度。在MOA平台上对真实与模拟数据流进行了实验，结果表明本文提出的方法是有效的。

参考文献：

[1] BEYAZIT E，ALAGURAJAH J，WU X D. Online Learning from Data Streams with Varying Feature Spaces [J].Proceedings of the 33rd AAAI Conference on Artificial Intelligence，2019，33（1）：3232-3239.

[2] SCHNEIDER J，VLACHOS M. On Randomly Projected Hierarchical Clustering with Guarantees [C]//Proceedings of the 2014 SIAM International Conference on Data Mining（SDM）.Philadelphia：SIAM，2014：407-415.

[3] BIFET A，GAVALDA R，HOLMES G，et al. Machine learning for data streams：with practical examples in MOA [M].USA：Massachusetts Institute of Technology press，2017.

[4] SCHNEIDER J，VLACHOS M. Fast parameterless density-based clustering via random projections [C]//CIKM’13：Proceedings of the 22nd ACM international conference on Information & Knowledge Management.New York：ACM，2013：861-866.

[5] ANDRÉS-MERINO J，BELANCHE L. StreamLeader：A New Stream Clustering Algorithm not Based in Conventional Clustering [C]//Artificial Neural Networks and Machine Learning–ICANN 2016.Barcelona：September，2016：208–215.

[6] YE M，LIU W F，WEI J H，et al. Fuzzy c-Means and Cluster Ensemble with Random Projection for Big Data Clustering [J/OL].Mathematical Problems in Engineering，2016（1）：1-13.

[7] HE Y，WU B，WU D，et al. Online learning from capricious data streams [C]//Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence，Macao：IJCAI，2019：2491-2497.

[8] LOSING V，HAMMER B，WERSING H，et al. Randomizing the Self-Adjusting Memory for Enhanced Handling of Concept Drift [C]//2020 International Joint Conference on Neural Networks（IJCNN）.Glasgow：IEEE，2020：1-8.

[9] KRANEN P，ASSENT I，BALDAUF C，et al. The ClusTree：indexing micro-clusters for anytime stream mining [J].Knowledge and Information Systems，2011，29（2）：249–272.

[10] 朱穎雯，陈松灿.基于随机投影的高维数据流聚类 [J].计算机研究与发展，2020，57（8）：1683-1696.

作者简介：李志杰（1964—），男，汉族，湖南永兴人，博士，副教授，研究方向：大数据在线学习;廖旭红（1997—），女，汉族，湖南醴陵人，硕士研究生在读，研究方向：数据流聚类;刘基旺（1997—），男，土家族，湖南永顺人，硕士研究生在读，研究方向：数据流分类;江华（1997—），男，汉族，安徽合肥人，硕士研究生在读，研究方向：数据流分类。