搭建中职生理解函数概念的桥梁

曹娟

摘要：针对中职学生理解函数概念时存在较大难度的问题，笔者认为建立相关的桥梁很重要。这个桥梁的一头是明悉初中函数的基本知识，另一头是凸显高中函数的鲜明特点。复习初中函数概念时，强化函数表现形式中的解析式法，淡化函数的不给出具体解析式的抽象形式，完善学生的认知结构;学习高中函数概念时，突出其与初中函数的异同点，增强学生的辨识度。从初中和高中两头发力，教与学才能发挥出最大效能。

关键词：中职生  函数概念  桥梁

对于中职生来说，挖掘数学学习潜力需要建立一座便于通行的桥梁。让这座桥梁真正起到使学生消除畏难思想、乐于全力以赴的作用，我认为可以从基本点、闪光点、特异点三个方面入手。简言之，基本点是指带领学生走出基本概念的盲区，闪光点是指善于发现学生的比较优势，特异点是指通过变式等方法识别近似内容的差异点。

数学函数概念的学习是高中生的一大痛点。高中函数概念和初中函数概念相比有三个转折点，即常数到变量的转折，静态到动态的转折，一元到二元的转折。众所周知，常数是静态的知识，变量是动态的知识，帮助中学生把静态的感性认识上升为动态的理性认识，把对一元的认识上升到对二元的认识甚至多元的认识，一直以来都是教师孜孜以求的目标。本文拟从以下几方面谈谈自己的做法。

一、中职生学习函数概念出现的问题

由于文化课基础薄弱，很多中职生早已淡忘了初中函数概念，甚至根本就不懂函数知识，一提函数就有一种模模糊糊、说不清楚的感觉，仅会举出常见的函数表达式，如y=2x、y=x+2x+1、y=1/x，也就是说他们将函数概念具体化，具体成函数表达式，弱化或淡忘了函数的本质属性（对应关系），而高中函数概念恰恰是在保留函数本质属性的基础上，推广函数概念，所以中职学生自主学习函数概念时就会出现旧伤未愈新伤又来的双难局面。

二、影响中职生理解函数概念的因素

首先，是函数概念本身的原因。“变量”的动态性，函数关系的两元性，呈现形式的多样性，以及函数符号的抽象性都比较难懂。

其次，是学生认知水平不足的原因。理解力达不到，不能把文字语言、符号和图形相互转换;思维水平低，学生的认知结构中数与形、动与静基本分离，不善于运用思维去理解运动变化的现象;抽象与具体的辩证认知不一致，从而难以理解函数的概念。

三、帮助中职生理解函数概念的方法

（一）抓住基本点，讲清初中函数概念

1.强化函数关系式法，消除抽象性对学生的负面影响

函数表达式是学生接触最多、记忆最牢，又是函数关系具体化的一种形式，能够具体地反映变量间的依赖关系，这也是学生为什么一提函数便会举出函数表达式的原因。因此，我们遵循认知规律，从学生角度出发，强化了列函数表达式的過程，让学生充分感受到函数表达式与方程的相似之处，感受变量间的等量关系;强化求函数值的过程，让学生充分感受求函数值与求代数式值的相同之处，借等量关系理解对应关系。这样把前后知识贯通起来，能够完善学生的知识结构，有效地消除抽象性对学生学习函数的影响。

如给出两个量x和y，当x=1时，y=2;当x=2时，y=4，当x=3时，y=6，当x=4时，y=8…依此类推，学生自然会推出y=2x（一次函数）;给出两个量x和y，当x=1时，y=1;当x=2时，y=4;当x=3时，y=9;当x=4时，y=16…依此类推，学生也会得出y=x2（二次函数）;倍数、平方、倒数关系，学生已经熟悉，易于掌握，又能体现一元到二元的转变，具体地反映函数关系，有效克服了抽象理解函数的难题。

2.强调变量，巩固变化意识

简单的数据不能使学生有效理解变量的概念，不利于学生变量意识的形成，因此要继续向学生补充熟知的具体实例，如下所示。

问题1：我们以100米/分的速度骑车去郊游，那么行驶的路程s与时间t之间的关系是_________。

（1）这个问题中有哪几个量？

（2）根据关系式填写下表。

问题2：电影票单价10元/张，票房收入y元与x张售票张数的关系式_________。

（1）这个问题中有哪几个量？

（2）根据关系式填写下表。

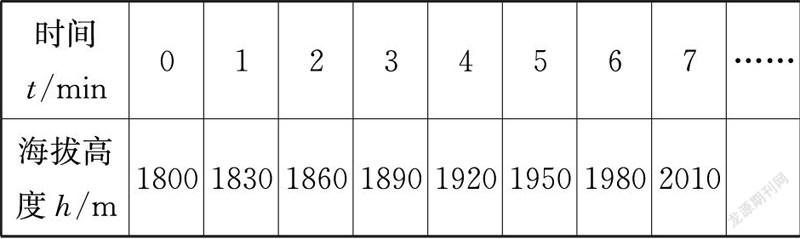
问题3：从1800米处放飞热气球，在一段工作时间内，它匀速上升，所到达的海拔高度h与以及上升时间t，如下表：

（1）这个过程中，有哪几个量？

（2）热气球平均每分钟上升的高度是多少？

（3）列出气球高度h与时间t之间的关系式。

通过以上三个问题找量，回忆了变量和常量的概念;通过填表初步回忆了变量间的对应关系。

3.强调对应关系，抓住函数本质属性

函数还有一个重要属性——对应关系，因此还要培养学生把注意力从数量关系转移到对应关系上，在表达关系式和填表格的基础上，继续引入初中教材里的“用电负荷曲线图”，并提出用电负荷与时间的关系，提醒学生函数概念强调的是对应关系，而不是单一的数量关系，关系式只是函数的表达形式之一，而不是函数的属性，从而全面揭示出函数的本质属性。

（二）发现闪光点，归纳函数概念要素

对于比较简单的知识，如果学生能理解清楚就应当作为闪光点，及时表扬、鼓励学生。比如引导学生分析以上几个案例，归纳函数概念要素。相比之下，尽管有不同的表现形式，但它们都具有共同的特点：一是存在两个变量;二是两个变量之间，有一种对应关系;三是每给定一个变量的值，根据对应关系，就确定了另一个变量（借助列出的等式，由求代数式的值体现出来，对应关系具体化）。

（三）突出特异点，对比高中函数概念

对初中函数概念的全面复习，提高了学生认识函数的能力，为介绍高中函数概念铺设了一个台阶，让高中函数概念的产生有了依据，让学生的知识结构形成链条。因此，我们提出从集合的角度出发，去理解函数，展示高中函数概念，将其与初中函数逐条进行对比分析。

（1）自变量取值范围为数集D，即把自变量的取值范围可以看成一个集合。

（2）按照某个对应法则f，常见的是y=2x，y=1/x，y=x2+2x+1，即初中的函数关系式。

（3）y=f（x）即关系式通常写成f（x）=2x，f（x）=1/x，f（x）=x2+2x+1

以上分析成功地指出了初中函数概念与高中函数概念的异同点：相同点是函数的本质属性没变（两个变量与对应关系），不同点是函数符号改变了。

当然，对于这样比较抽象、难度又大的问题，需要老师充分发挥自己的主导作用，将内容分解，降低难度，适当提示学生，给学生铺设台阶，给予学生帮助。

总之，我们要借助于列方程来列函数关系式，强化函数关系的具体形式，淡化函数概念的抽象形式，借求代数式的值求函数值，体现对应关系，完善学生知识结构，以有效消除抽象性对学生学习的影响;借助于初中函数概念来介绍高中函数概念，使前后知识贯通起来，实现降低学习难度、增强识别度的教学目的。

参考文献：

课程教材研究所，中学语文课程教材研究开发中心.义务教育课程标准实验教科书教师教学用书[M].北京：人民教育出版社，2007.

责任编辑：黄大灿