全国和区域蔬菜价格走势特征及影响因素
杨 娟 钱婷婷 郑秀国 赵京音 许叶颖
(1.上海市农业科学院 农业科技信息研究所,上海 201403;2.上海数字农业工程技术研究中心,上海 201403)
当前我国蔬菜产量从数据上分析呈现供过于求的现象[1],人均年蔬菜产量达到504 kg,同期2003—2016年蔬菜价格总体呈上涨趋势[2-3],阶段性涨跌现象频现[4],2017、2018年蔬菜价格相对有所下跌。价格波动频繁影响菜农收益,反映了蔬菜产业供给侧结构性调整的必要性。
价格是生产决策的风向标,李锁平等[1]研究发现蔬菜种植面积与当年蔬菜价格和上年蔬菜价格都有关联,实际蔬菜价格年内、年际间和区域间差异都较大,目前农产品价格研究更多的关注于大宗农产品年际间的变化及其影响因素[5],涉及蔬菜价格年内和年际间、区域间差异研究的较少。
对于耐储存农产品,全国不同区域价格差异不大,而对于蔬菜这类鲜食农产品,区域间价格差异较大,因此应分类管理[6]。蔬菜价格年度内波动也较大,季节性特征强,尤其是生长季短的绿叶类蔬菜[7-8],市场变化影响因素多,供求变化、宏观经济如居民消费价格指数[9]、人均可支配收入[10]、生产成本、运输成本、天气[11-12]等都对其有较大影响,甚至汇率变动都会影响到农产品价格[13]。总的来说,蔬菜的季节性、种类性和区域性供过于求是导致蔬菜价格波动频繁、价格下跌的主要原因,归根溯源还是信息的不对称和商品流通的不畅[4]。
农产品价格分析的方法有比较分析方法,有回归分析法,如向量误差修正模型[5]、向量自回归VAR模型[14]等,用面板VAR模型甚至可以分析相关的多项因素如天气、国际市场因素等对价格波动的影响[5,14]。而最常见的农产品价格分析工具还是时间序列分析方法,时间序列分析中的移动平均法、季节指数平滑法、差分自回归移动平均法(ARIMA)等都是较为常用也是效果较好地价格分析方法[15-17],不仅可以分析出农产品价格随时间的变化特征,还可以很方便地预测未来价格。
为研究蔬菜价格的区域差异性,本研究以上海蔬菜价格为例,对全国蔬菜价格和区域蔬菜价格的差异进行实证分析,在分析区域蔬菜价格与全国蔬菜价格之间的走势特征的基础上,采用时间序列分析方法分析全国和上海蔬菜价格的季节性、波动性的异同以及价格影响因素的差异,以期为区域蔬菜生产调控管理和销售策略制定提供科学指导。
1 数据来源
全国蔬菜价格数据来源于国家农业农村部信息中心农产品市场信息数据仓库,全国蔬菜价格采集自全国490个批发市场,采集频率为每日1次,本研究以该数据仓库中28种规模销量蔬菜的平均价格为全国蔬菜价格开展分析,分析时间为1995—2018年。上海蔬菜价格数据来源于上海市农业农村委“上海农产品价格监测与分析预测系统”,蔬菜价格采集自上海市8个农产品一级批发市场,采集频率为每日1次,本研究以该系统数据库中26种规模销量蔬菜的平均价格为上海蔬菜价格开展分析,分析时间为2010—2018年。
2 研究方法
2.1 基本统计特征分析方法
用算术平均数法获得蔬菜日平均价格、月平均价格和年平均价格,分别简称为日均价、月均价和年均价,计算月均价和日均价的标准差、变异系数、中位数、众数、偏度和峰度,初步分析蔬菜价格的波动性特征。
利用EViews软件分析全国和上海蔬菜价格的季节性、趋势性和不规则性特征。运行Census X-12季节调整模型,将蔬菜月均价时间序列数据分离成季节因子序列(Seasonal factors)、趋势循环序列(Trend-cycle)和不规则序列(Irregular component),趋势循环项再运用Hodrick-Prescott滤波法进一步分离得到趋势序列(Trend)和循环序列(Cycle),其中季节因子序列可以分析价格的季节波动规律,趋势序列可以分析价格随时间的走势特征,不规则序列可以分析价格是否受一些不规律因素的影响或某些因素的不规律性影响。
2.2 影响因素分析方法
2.2.1前期价格的影响分析
前期价格对全国和上海蔬菜价格数据序列的影响采用时间序列分析模型法进行分析,选用求和自回归移动平均(ARIMA)模型、季节性求和自回归移动平均(SARIMA)模型、Holt-Winters指数平滑模型分别建立全国和上海蔬菜月均价的时间序列分析模型,根据模型结构和参数值分析蔬菜价格的特征。模型参数可运用EViews软件运算获得。
1)ARIMA模型结构。ARIMA模型的结构为ARIMA(p,d,q),表示时间序列{xt}的d阶差分是一个平稳可逆的ARMA(p,q)模型,模型结构为:
xt=Ø0+Ø1xt-1+…+Øpxt-p+
εt-θ1εt-1-θ2εt-2-…-θqεt-q
(1)
式中:Ø0为常数,Ø1,Ø2,…,Øp和θ1,θ2,…,θq为系数;p为自回归阶数;q为移动平均阶数,εt为时间序列{xt}自回归后的残差序列,是均值为0的白噪声序列。
2)SARIMA模型结构。SARIMA模型的结构为SARIMA(p,d,q)×(P,D,Q)s,表示时间序列{xt}经过d阶差分和D阶季节差分后是一个平稳可逆的ARMA(p,q)模型,模型结构为:
(1-Ø1B-Ø2B2-…-ØpBp)·

c+(1-θ1B-θ2B2-…-θqBq)·
(1-Θ1Bs-Θ2B2s-…-ΘQBQs)εt
(2)
式中:p、d、q分别为非季节的自回归阶数、差分阶数和移动平均阶数。s为季节周期。P、D、Q分别为季节的自回归阶数、差分阶数和移动平均阶数。Ø1,Ø2,…,Øp;Φ1,Φ2,…,ΦP;θ1,θ2,…,θq;Θ1,Θ2,…,ΘQ均为系数。c为常数。
3)Holt-Winters指数平滑模型结构。Holt-Winters指数平滑模型分为季节因子子模型和趋势子模型,季节因子子模型获得的季节因子值采用乘法形式与趋势子模型结合获得最终的模拟值。2个子模型的结构分别为:
(3)
ln(xt_sa)=d+eT
(4)
式中:at为序列的水平部分;bt为序列的趋势部分;st为序列的季节因子;π为一个季节的周期长度;α,β,γ为平滑系数,介于0和1之间;xt_sa为去除了季节因子的蔬菜月均价序列;T为时间趋势,序列第一期取值1,第二期取值为2,以此类推;d、e为模型参数。
2.2.2经济因素的影响分析
采用相关性分析法和回归分析法分析价格与各影响因素的关系。本研究选择上一年的蔬菜年均价(Price,PR(-1))、蔬菜产量(Production,P)、蔬菜总需求量(Total cosumption,TC)、蔬菜生产成本(Production cost,PC)、居民消费价格指数(Consumption price index,CPI)、人均可支配收入(Per capita disposable income,PCDI)、城镇化率(Urbanization rate,UR)7个指标分析蔬菜年均价与这些影响因素之间的关系。蔬菜产量等经济指标全国数值采用1995—2018年数据,数据来源于国家统计局数据库[18],上海数值采用2010—2018年数据,数据来源于《上海统计年鉴》[19]。
回归分析选择PR(-1)、PC、CPI、PCDI、UR 这5个指标作为自变量,回归方程如下:
Xt=aIt+C
(5)
式中:Xt为应变量蔬菜年均价;It为自变量;a为变量的系数;C为常数。
3 结果与分析
3.1 数据特征分析
3.1.1基本统计特征分析
1996—2018年我国蔬菜年均价呈现先下降后持续上升的趋势,但2017—2018年蔬菜年均价较为平稳甚至有所降低(图1)。具体而言,1995—2002年我国蔬菜年均价呈下降趋势,平均每年下降3.3%,2003年开始,蔬菜年均价持续上涨到2018年,平均每年上涨14.6%,这其中2014年和2017年较为特殊,价格较上年有所下降,分别下降了2.0%和7.8%。

图1 全国和上海蔬菜年均价走势
2010—2018年上海蔬菜年均价整体呈平稳上升趋势,低于全国水平,与全国蔬菜年均价走势相同,平均每年上涨2.1%,同期全国蔬菜年均价每年上涨3.0%。其中,2016年上海蔬菜价格涨幅最大,较上年上涨了9.9%,高于全国的9.5%;2017年跌幅较大,较上年下降了11.2%,高于全国水平。
从具体数值(表1)看,2010—2018年全国蔬菜月均价为4.3 元/kg,而同期上海蔬菜月均价为3.7 元/kg;全国和上海蔬菜月均价的标准差分别为0.7、0.6 元/kg,变异系数分别为15.1%、16.5%;而日均价的标准差分别为0.7、0.8 元/kg,变异系数分别为15.7%、23.5%。可以看出,日价格波动较月价格频繁,上海蔬菜价格的波动较全国蔬菜价格频繁。从中位数、众数、偏度和峰度等整体看,分析期间内全国和上海蔬菜价格数据序列均表现为向右的正偏态分布,数据波动频繁,呈现尖顶峰形态。

表1 全国和上海蔬菜价格数据统计特征分析
图2示出全国和上海蔬菜月均价及日均价的走势。可以看出,我国蔬菜价格波动频繁,日均价的波动幅度尤其大。上海蔬菜日均价在2016-09—2017-02这一时期价格较低,明显低于全国水平,分析具体原因,主要是这一时期我国江南地区温度高于常年,且天气晴好,利于蔬菜的生长,导致蔬菜供过于求,价格大大低于历史同期。

图2 全国和上海蔬菜月均价(a)及日均价(b)走势
3.1.2季节性特征分析
利用时间序列分析的Census X-12乘法和Hodrick-Prescott滤波法对全国和上海蔬菜月均价的分析结果表明,我国蔬菜存在明显的季节性变动特征(图3),全国蔬菜月均价在每年2月到下一年2月之间的时段内蔬菜价格呈 “V”形波动规律,2月较高,随后开始下降,至6月下降到一年的最低值,随后又开始上升,9、10月有时有一个小低谷,但波动幅度不大,之后又一路上升至次年2月达到顶峰(图3(a))。而上海蔬菜月均价在每年3月至下一年3月呈 “W”形波动规律,3月较高,随后开始下降,到6月降至一年的最低值,随后又开始上升,9月上升到另一个波峰,幅度比3月的略小,之后又下降到11月的波谷,然后又回到3月的最高峰(图3(b))。对比全国和上海蔬菜月均价的季节因子特征,2010—2018年全国蔬菜月均价的季节因子先扩大后缩小,而上海蔬菜月均价的季节因子呈缩小的趋势,这可能是由于上海蔬菜仅来源于全国部分蔬菜产区,也反映了全国和区域蔬菜市场特征的不同。
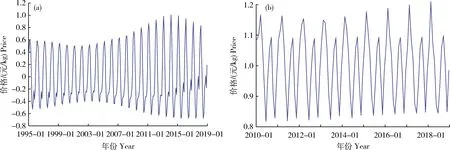
图3 全国(a)和上海(b)蔬菜月均价季节因子序列曲线
图4示出全国和上海蔬菜月均价趋势循环序列经H-P滤波分解后的趋势曲线和波动曲线,从趋势曲线来看,全国蔬菜月均价1995—2002年呈下降的趋势,2003年开始月均价走势上涨,近些年较为平稳,这与图1所示的全国蔬菜年均价走势一致,上海蔬菜月均价自2010年至今基本较为平稳。从波动曲线来看,分离掉趋势曲线序列和不规则序列(图5)后的波动曲线表现出平稳的季节性波动特征。

图4 全国(a)和上海(b)蔬菜月均价趋势循环序列H-P滤波分解
图5示出全国和上海蔬菜月均价的不规则项序列曲线。可以看出,全国和上海蔬菜月均价都存在不规则性,上海蔬菜月均价的不规则性更强。从蔬菜产品的特征以及影响蔬菜市场的现实因素进一步综合分析,引起蔬菜价格不规则性波动的原因很多,首先蔬菜产品为鲜品,不耐储存,其次蔬菜生长季短,生产和运输销售过程中受夏季高温、冬春低温、阴雨、干旱等自然灾害天气影响大,再次还会受到节假日、舆论导向等社会经济因素的影响。
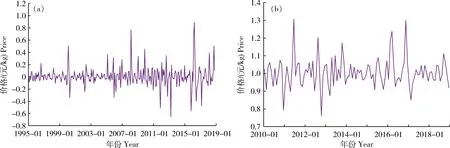
图5 全国(a)和上海(b)蔬菜月均价不规则序列
3.2 时间序列分析模型
3.2.1全国蔬菜价格时间序列分析模型
全国蔬菜月均价为非平稳序列,月均价呈现先下降后上升的趋势,其一阶差分序列为平稳序列,因全国蔬菜月均价具有季节性波动特征,可以建立ARIMA模型、SARIMA模型和Holt-Winters指数平滑模型来分析前期价格影响。
经过多种模型参数取值组合模式的测试分析,根据模型显著性检验和模型参数显著性检验,得出ARIMA(3,1,4)、SARIMA(1,1,1)×(3,1,3)12、Holt-Winters指数平滑模型都是较为适合全国蔬菜月均价的时间序列分析模型,从表2可以看出,模型常数和各变量的系数显著性检验概率值(prob.)都小于0.15,通过了检验。进一步对比ARIMA模型和SARIMA模型的模型拟合度、残差平方和、AIC值和BIC值可以看出,SARIMA模型略优于ARIMA模型。

表2 全国蔬菜价格各类型时间序列分析模型的结构及其系数、模型检验值
因Holt-Winters指数平滑模型的最终模拟结果是趋势模型结果与季节因子的乘积,进一步对比3种模型模拟的1995—2018年全国蔬菜月均价的模拟值与实际值的对比效果,可以看出,SARIMA模型的RMSE值、MAE值、MAPE值也都低于其他2种模型(表3),说明SARIMA模型用于分析预测全国蔬菜价格最好。

表3 全国蔬菜价格各类型时间序列分析模型的预测效果分析
3.2.2上海蔬菜价格时间序列分析模型
上海蔬菜月均价也是一阶差分序列为平稳序列,同样具有季节性波动特征,因此选择了ARIMA模型、SARIMA模型和Holt-Winters指数平滑模型分析前期价格的影响。
经过多种模型参数取值组合模式的测试分析,根据模型显著性检验和模型参数显著性结果,得出ARIMA(4,1,1)、SARIMA(3,1,3)×(2,1,0)12、Holt-Winters指数平滑模型都是较为适合上海蔬菜月均价的时间序列分析模型,由表4可以看出,模型常数和各变量的系数显著性检验概率值都小于0.15,通过了检验。进一步对比ARIMA模型和SARIMA模型的模型拟合度、残差平方和、AIC值和BIC值可以看出,SARIMA模型略优于ARIMA模型。

表4 上海蔬菜价格各类型时间序列分析模型的结构及其系数、模型检验值
因Holt-Winters指数平滑模型的最终模拟结果是趋势模型结果与季节因子的乘积,因此进一步对比3种模型模拟的2010—2018年上海蔬菜月均价的模拟值与实际值的对比效果,可以看出,ARIMA模型的RMSE值、MAE值、MAPE值都低于其他两种模型(表5),从模拟效果看,ARIMA模型较好。
表5 上海蔬菜价格各类型时间序列分析模型的预测效果分析
3.3 影响因素分析
3.3.1价格与各影响因素的相关性分析
全国蔬菜年均价受上期价格的影响较大,表明全国蔬菜价格年际间延续的特点比较明显,此外全国蔬菜年均价与蔬菜产量、蔬菜总需求量、生产成本、居民消费价格指数、人均可支配收入、城镇化率也都有较高的相关关系(表6)。而上海蔬菜年均价与上期价格的相关性小于全国蔬菜年均价,与居民消费价格指数、蔬菜总需求量、人均可支配收入相关性较强,与蔬菜产量呈负相关。

表6 全国和上海蔬菜价格与各经济因素间的相关系数
3.3.2价格与各影响因素的单因素回归分析
全国蔬菜年均价与上期价格、生产成本、居民消费价格指数、人均可支配收入、城镇化率呈现正相关关系,回归方程的系数均为正值(表7),表明全国蔬菜价格随着这些因素的增大/多而提高,随着这些因素的降低/减少而降低,其中与居民消费价格指数CPI的拟合度最高,其次是上年价格,这与市场调查中得到的结论一致,蔬菜销售者定价的主要依据是维持生活成本所需商品的价格走势和变化幅度。
上海蔬菜年均价与上期价格、生产成本、居民消费价格指数、人均可支配收入呈现正相关关系,回归方程各影响因素的系数均为正值(表7),表明上海蔬菜价格随着这些因素的增大/多而提高,随着这些因素的降低/减少而降低,其中与居民消费价格指数CPI的拟合度最高,其次是人均可支配收入。
表7 全国和上海蔬菜价格单因素回归模型系数和模型拟合度
4 结论与讨论
本研究结果表明,上海蔬菜年均价低于全国蔬菜年均价,月均价和日均价的波动性和不规则性高于全国蔬菜。季节性波动是我国蔬菜价格的主要特征,上海蔬菜价格尽管与全国蔬菜价格一样都具有季节性,但季节特征不同。与前期价格的关联性分析结果表明,全国蔬菜月均价用SARIMA模型模拟效果最好,参数取值反映了全国蔬菜价格与前3年同月价格、当年前1月价格较高的关联性,而上海蔬菜月均价用ARIMA模型模拟效果较好,参数取值反映了上海蔬菜价格与当年前4个月价格的关联性最高,而其SARIMA模型的参数取值表明上海蔬菜还与前2年同月价格也有较高关联性。经济因素中,居民消费价格指数对全国蔬菜价格和上海蔬菜价格的影响都最大,其他经济因素如生产成本、人均可支配收入、城镇化率也对蔬菜价格有一定影响。
我国蔬菜价格受蔬菜作物生长特性影响,呈现明显的季节性特征。在一年内的总体变化规律是:每年11月至次年2月为蔬菜上市淡季,蔬菜价格相对较高;3—4月,温室、大棚蔬菜陆续产出,但其数量不大,对蔬菜价格的影响较小,蔬菜价格虽有所下降,但仍处于高位;6—10月蔬菜旺产旺销的季节,露地、温室、大棚蔬菜全面供应,受供求关系影响,蔬菜价格降至最低;10月末,露地蔬菜基本销售结束,蔬菜价格逐步回升。蔬菜月度价格季节波动性明显,而日度价格受诸多因素的影响,表现出强烈的不规则性,其中天气和受天气影响的运输条件对价格影响最大,有研究发现不仅台风暴雨、连阴雨[11-12]对蔬菜价格有影响,温度[14]尤其是高温对蔬菜价格也有较大影响。气象因素主要通过影响蔬菜作物的适生性间接影响供应量来影响价格,或者通过影响运输成本、运输条件等间接发挥作用,使得蔬菜价格表现出明显的不规则性特征,气象对价格的定量化影响是蔬菜价格研究的难点,需要加强研究。
尽管上海蔬菜年均价低于全国蔬菜年均价,但从实际的市场运行看,作为大型销区市场,上海蔬菜市场产品仍然十分丰富,这源于大市场带来的规模效益。上海和全国蔬菜月均价的最适时间序列分析模型不同,说明了上海蔬菜价格受外来蔬菜量价的影响较大,而与本地的生产量相关性不强。由于不同区域的价格与全国价格相比有一定差异性,因此以区域为尺度开展农产品市场信息分析研究具有现实意义,可科学指导生产者更好的安排生产计划,管理者更科学的制定农业政策,从而保障蔬菜的稳定供给和市场价格的稳定,解决蔬菜生产当前存在的季节性供过于求、区域性供过于求,蔬菜生产类别难以满足市民日益增长的种类多样化需求等问题。
需要指出的是,蔬菜价格研究中存在2点困难:一是系统性、长期连续性的数据欠缺,由于数据获取的不易以及监测的中断,现有研究报道中所跟踪的蔬菜价格时间均不长[3,14-15,20],建议国家和各级政府重视蔬菜市场信息数据的监测与共享;二是蔬菜价格与影响因素的定量关系模型的建立较为困难,由于影响因素与价格的内生性关系,影响因素之间的多重共线性问题,不能建立包含所有影响因素的定量回归模型,因此结构性的局部均衡模型将是蔬菜市场信息进一步研究的重要方法。

