耦合不同年龄层接触模式的新冠肺炎传播模型*
王国强 张烁 杨俊元† 许小可
1) (山西大学复杂系统研究所,太原 030006)
2) (山西大学,疾病防控的数学技术与大数据分析山西省重点实验室,太原 030006)
3) (大连民族大学信息与通信工程学院,大连 116600)
搜集广东省自1月23日到2月16日期间944例新冠肺炎样本信息.对确诊人群进行年龄特征分析,将人群分为儿童组(0—5岁)、青少年组(6—19岁)、中青年组(20—64岁)、老年组(65岁及以上),耦合不同年龄层的接触模式,建立离散年龄结构新冠肺炎模型,得出模型的基本再生数及最终规模.通过蒙特卡罗数值算法(MCMC)辨识模型的参数、拟合累计病例数、计算消亡时间、感染峰值及到达时间等有关生物量.研究发现中青年人群感染人数最多; 相比于居家模式,社区模式下中青年人群感染峰值上升41%,峰值推迟一周到达.通过分析不同年龄层的最终规模在对应年龄层的占比,发现老年人的易感性较高,青少年的易感性相对较低.在居家模式下,若各年龄层患者能及时就诊,住院峰值将进一步减少,但住院高峰将提前一周到达.此模型可揭示个体接触行为对新冠肺炎的传播的影响,定量评价居家隔离措施的有效性.
1 引 言
新冠肺炎“coronavirus disease 2019” (COVID-19)肆虐全球10个多月以来,截至目前已有7000多万人确诊,170多万人死亡,给人类的健康和生活带来极大的危害.广东作为中国人口第一大省、经济强省,人口密集且流动频繁,感染风险颇大.截至2020年7月16日,广东省新冠肺炎累计确诊 1650 例,新增病例均为输入性病例,疫情基本得到控制.这主要得益于广东各级政府及时启动新冠肺炎疫情防控一级响应[1],如封城、限制或者停止集会、居家隔离、佩戴口罩等一系列措施.在此基础上,了解和掌握新冠肺炎的流行特征和内在传播机制是有效遏制新冠肺炎再次爆发传播的关键.
分析广东省2020年1月9日到2月16日944例新冠肺炎患者的详细病例数据信息(年龄、性别、接触史、症状、症状出现时间、住院确诊时间等),发现大多数患者以发热为主要临床症状,所占比例为73.31%,而少数患者伴有咳嗽、头晕、肌肉酸痛、乏力等症状; 男性患者占比49.79%,女性患者占比50.21%.通过对广东省每日新增病例分段统计 (如图1 所示),发现 0—5 岁、6—19 岁、20—64岁、65岁及以上各年龄组每日新增病例分别于1月31日、2月1日、1月27日及2月2日到达高峰; 由图1 发现,20—64 岁每日新增病例高峰到达时刻早于其他组别,且变化幅度明显高于其他组别.
为了更直观地观测每日新增确诊病例年龄构成,图2给出了各年龄组每日新增病例占当日新增总病例百分比.发现每日新增病例占当日新增总病例的百分比20—64岁超过80%,65岁及以上约为15%,0—19岁仅为 5%.广东省新冠肺炎患者分布呈现明显的年龄异质性.如何利用数学模型揭示新冠肺炎传播的年龄异质性,对新冠肺炎的优化控制至关重要.

图1 广东省各年龄组每日新增病例折线图Fig.1.Line chart of new cases for each age group in Guangdong province.

图2 广东省各年龄组每日新增病例占当日新增总病例百分比图Fig.2.Chart of the percentage of new cases for each age group in the total new cases of each day in Guangdong province.
现有新冠肺炎模型主要包括以数据驱动的统计模型[2-5]及通过机理分析建立的动力学模型[6-8],统计建模以数据驱动为特点,能直观描述疾病的发生和发展过程,如曹文静等[5]构建了安徽省疫情发展后期的自回归传播模型,为新冠肺炎疫情的传播早期预测预警提供参考.动力学模型主要发掘疾病传播的内在传播规律,评估和预测疾病流行特征.李盈科等[6]详细阐述了几类新冠肺炎动力学模型及其在早期疾病防控方面的作用,模型假设人群的接触是均匀混合的,忽略了接触行为的异质性.了解和掌握不同年龄段个体接触模式可以更精准地刻画传染病传播的传播途径,是传染病建模的重要组成部分[9-11].广东省采取了严格的管控遏制新冠肺炎的传播,该措施改变人的行为模式及活动范围.本文考虑以个体家庭为中心,将人群的活动距离分为家庭内部(居家模式)和家庭外0.5 km内活动范围(社区模式),并在两种模式下对不同年龄组之间的接触进行量化,得到不同模式下的接触矩阵,结合传播动力学模型,刻画新冠肺炎在不同人群间的传播.考虑各年龄层接触模式的异质性对提高新冠肺炎传播的认识及控制具有重要意义,并可提供理论依据.
近期,已有一些学者耦合社会接触模式和动力学建模方法来研究年龄异质性对新冠肺炎的影响[12,13].如Kiesha等[12]建立了一个离散年龄结构的SEIR 模型评估不同时间复工对新冠肺炎的影响.文献[13]评估不同年龄段的错峰复工感染新冠肺炎的风险.已有的结果主要讨论不同年龄间接触模式对新冠肺炎的风险评估,对数据的拟合及实际情况的预测略有欠缺.本文拟合广东省新冠肺炎各年龄层高维数据、辨识模型参数,揭示社会接触行为对新冠肺炎传播的影响,评估各种策略对新冠肺炎传播的影响.
2 模型假设和构建
2.1 模型假设
1) 2020年1月23日至2月19日时间跨度较短; 1 月 23 日距除夕仅一天,春运基本结束,而且各级政府已于1于23日实行封城,人口流动因素可以忽略.因此可忽略人口出生和自然死亡,不考虑人口迁移,假设广东省人口为固定常数.
2)自1月23日起,全国各地开始实行严格的居家式隔离,人与人之间主要以家庭单位接触,故假设广东省人群接触方式为家庭式接触.
3) 假设广东省的医疗资源充足,被确诊的染病者能得到及时救治.
4) 假设确诊者入院后被完全隔离,不再具有传染性.
2.2 模型构建
依据广东省新冠肺炎传播特征,将广东省人口分成0—5岁、6—19岁、20—64岁以及65岁及以上4个不同层次,刻画广东省新冠肺炎在儿童、青少年、中青年、老年人群中的流行特征.用N1表示0—5岁的总人口,N2表示6—19岁的总人口,N3表示20—64岁总人口,N4表示65岁及以上老年人的数量.依据SEIHR仓室建模理论,将第k(k=1,2,3,4)年龄段总人口Nk(t) 分成五种不同的人群,即易感者、潜伏者、染病者、确诊住院者和康复者,分别用Sk(t) ,Ek(t) ,Ik(t) ,Hk(t) 和Rk(t)表示.第k年龄阶段易感者的个体和j年龄阶段染病 个 体 平 均 接 触 数 为ckj,第k年 龄 段 和j年 龄段染病者接触数为总接触数为第k年龄段的易感个体以传播概率βk被感染而转变成潜伏个体Ek.潜伏个体经过 1 /α天潜伏变成染病个体.染病个体经过 1 /h天进入医院确诊.确诊住院个体经过 1 /γ天转化成康复个体.上述新冠肺炎状态间的转化可用如下微分方程组表述:
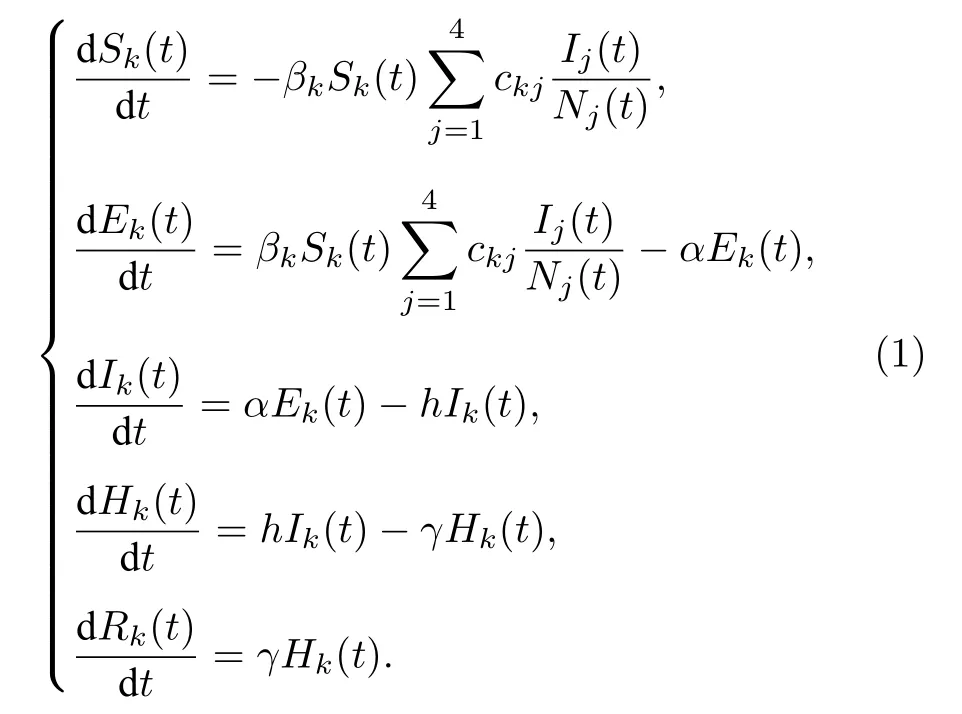
假设(1)式表示的模型1具有如下初值:

模型各参数的生物学意义及取值参见表1.第k个年龄组初始时刻的易感者数量、潜伏者数量、染病者数量、确诊者数量的具体取值见表2.

表1 参数定义和参数值Table 1.Parameter definitions and parameter values.
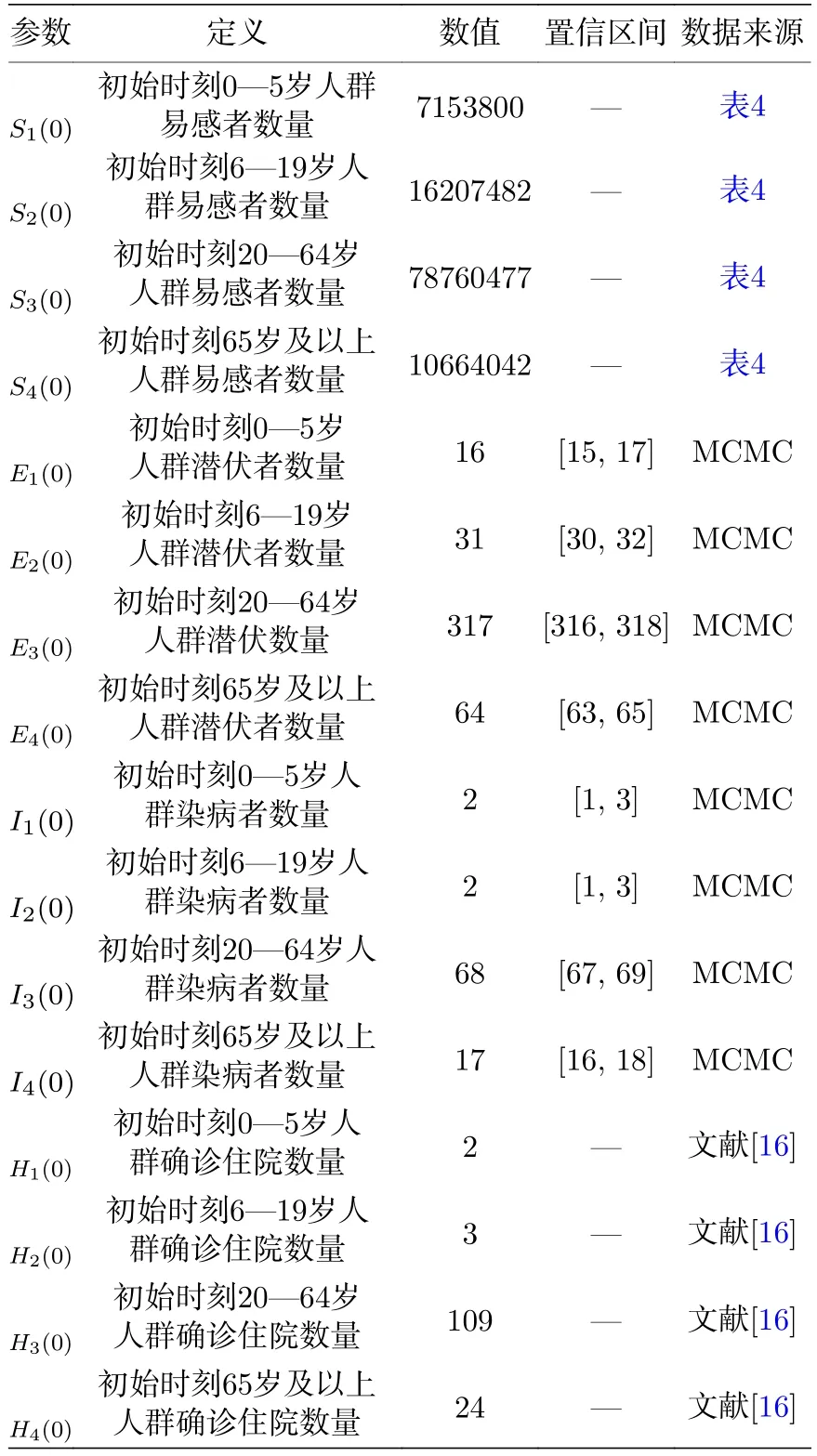
表2 变量生物学意义和变量初始值Table 2.The meaning of variables and initial values.
2.3 基本再生数
基本再生数是传染病防控中一个非常重要的量.基本再生数R0表示在一个全部都是易感者的环境中一个染病者在整个染病期内二次传染人数的平均值.在疾病传播初期,如果R0<1 ,疾病消亡; 否则,疾病流行.模型 1有惟一的无病平衡点

这里Nk(k=1,2,3,4) 分别表示广东省 0—5岁、6—19岁、20—64岁及65岁及以上人口数.
利用文献[17,18]计算模型1基本再生数.在无病平衡点P0处线性化模型1,定义
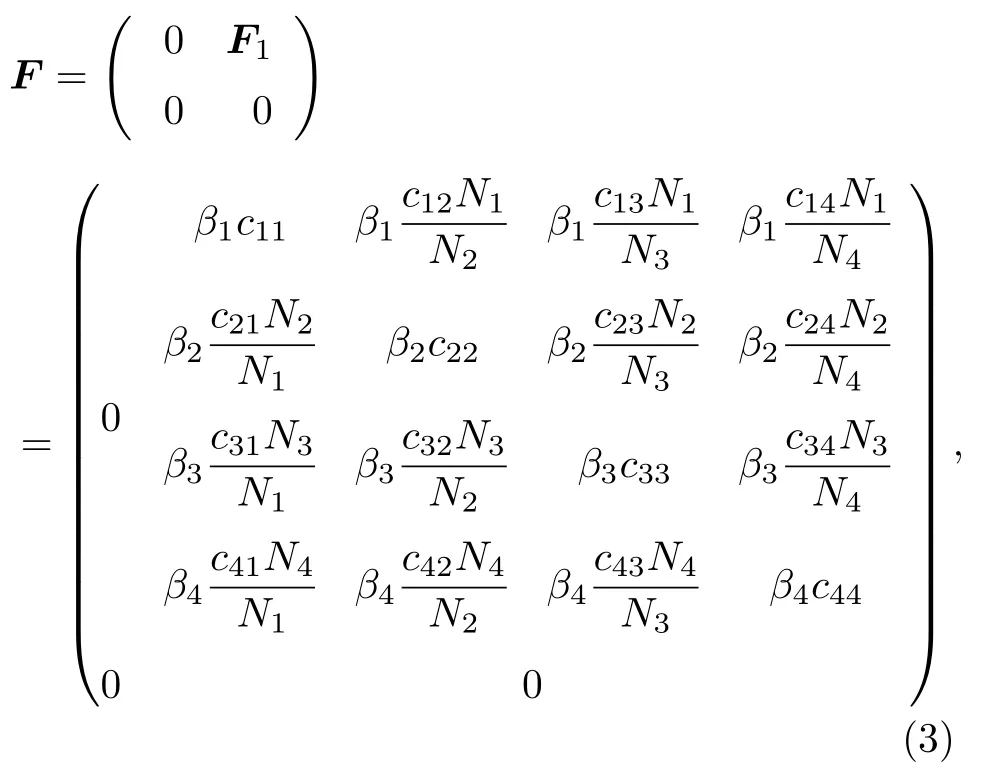
和
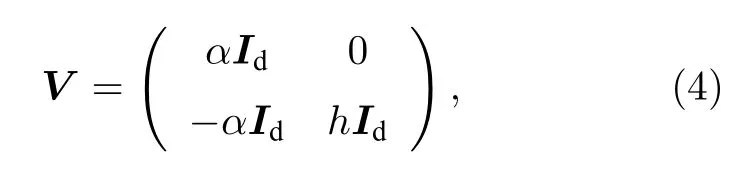
其中Id为 4×4 单位矩阵,0 为 4×4 零矩阵,

则

其中ρ表示矩阵的谱半径.
容易验证,当初值条件满足(2)式时模型1的解是非负的.注意到Nk(t)=Sk(t)+Ek(t)+Ik(t)+Hk(t)+Rk(t),那么故各年龄层人口数保持不变.从而区域

是模型(1)的一个正向不变集.
定理1假设矩阵F1不可约且R0<1 ,则无病平衡点P0全局渐近稳定.
证明由矩阵F1的不可约性,结合Perron-Frobenius[19]定理,矩阵F1存在一个单的特征根ρ(F1)=hR0和一个正的左特征向量ω=(ω1,ω2,ω3,ω4) ,满足ωF1=hρ(F1)ω=hR0ω.
令E=(E1,E2,E3,E4)T和I=(I1,I2,I3,I4)T,构建如下Lyapunov函数:

其 中ωk(k=1,2,3,4) 是hρ(F1) 对 应 特 征 向 量 的分量.
对L沿模型1解轨线求全导数得

令
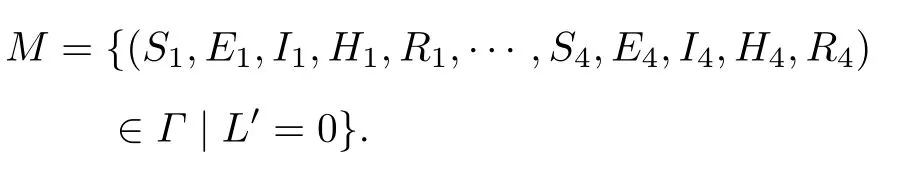
如果R0<1 ,由ω正性得到L′=0 的充要条件为I=0 .从而最大不变集M只包含惟一的无病平衡点P0.由 LaSalle 不变集原理[20]知,当R0<1时,无病平衡点P0是全局渐近稳定的.
定理1表明只要基本再生数小于1,就不会有新增新冠肺炎患者,疾病得以控制.
最终规模是指在整个疾病流行期间内感染的总人数.在传染病传播中,用来刻画疾病传播的危害程度.实际上由模型1可得,第k年龄层的累计病例数

即为各年龄组的最终规模.
首先,由模型1的第一个方程得出Sk(t) 单调递减,故Sk(∞) 存在.将模型 1 第一个方程分离变量积分得

其次,将模型1的前三个方程相加并积分得

最后,将(10)式代入到(9)式,得到模型1各年龄层最终规模为

其中Sk(∞) 表示第k年龄层易感者的最终规模.事实上,新冠肺炎的易感初始人群Sk(0) 已知; 若通过数据辨识模型参数βk和h、接触矩阵ckj及初值Ej(0)和Ij(0) ,根据 (11) 式可求出Sk(∞) ,进而得到第k年龄层的染病最终规模为Sk(0)+Ek(0)+Ik(0)-Sk(∞).
2.4 人口数据及部分参数值的确定
通过查阅中国2010年人口普查资料[21],得到2010年广东省各年龄层统计数据(见表3).
随后依据广东省2010年到2019年各年度人口增长和出生率[22],估算出现有年龄段人口分布(见表4).
由文献[23]可知新冠肺炎的平均潜伏期为5.2 天,故可以假设α=1/5.2 ; 根据国家卫健委新闻发布会[15],湖北省外患者从确诊住院到恢复出院时长约为10天,故可假设γ=1/10 .
从模型1不难发现,计算接触矩阵cij(i,j=1,2,3,4)非常关键[7,11].文献[14]对广东省城乡人口的出行和接触方式进行了调查,考虑个体活动范围(家庭内部和外部接触),得到了不同活动范围下的接触矩阵—家庭内部接触矩阵、以家庭为中心半径0.5 km内的接触矩阵及半径超过0.5 km的接触矩阵.本文将家庭内部接触矩阵定义为居家模式接触矩阵,将活动半径0.5 km以内和居家模式接触矩阵的和定义为社区模式接触矩阵.本次新冠肺炎的传播主要考虑儿童、青少年、中青年及老年人的流行病学特征和文献[14]各年龄层的划分相契合.
广东省于1月23日出台一系列严格的控制措施,如封城、居家隔离、停工、停课等,各年龄段的人群接触近似于居家模式.将文献[14]中家庭模式下的接触矩阵(图3(a))作为疫情期间采取居家隔离的接触矩阵.引入社区模式接触矩阵(图3(b))评估居家隔离措施对新冠肺炎的影响.接触矩阵中的元素ckj表示k年龄组的个体与j年龄组人群的接触数.

图3 (a) 广东省居家模式接触矩阵; (b) 广东省社区模式接触矩阵Fig.3.(a) Household-mode contact matrix of Guangdong;(b) community-mode contact matrix of Guangdong.

表3 2010 年广东省各年龄段人口 (单位: 1000 人)Table 3.The number of population for each age group of Guangdong province in 2010 (Unit: 1000).

表4 2019 年广东省各年龄段人口分布 (单位: 人)Table 4.The number of population for aggregated age groups in Guangdong province in 2019 (unit: person).
3 模型拟合结果
模型1中第k年龄组每日新增确诊病例为hIk(t),从而第T天的累计确诊病例为

结合马尔科夫链蒙特卡罗方法(MCMC)[24]拟合累计病例数据,同时采取Metropolis-Hastings(M-H)算法校准参数值和初值(见表1与表2).此算法随机模拟20000次,从第8000次模拟截断,计算后12000次模拟平均值.
基于各年龄组每日累计确诊病例,分别拟合0—5 岁 (儿童组),6—19 岁 (青少年组),20—64 岁(中青年组),65岁及以上(老年组)四个年龄组的累计病例随时间的变化图(如图4和图5所示).不难发现拟合的整体效果比较理想.但0—5岁年龄组的拟合偏差稍大,主要是由于0—5岁病例样本量较少,拟合噪声影响较强,导致实际数据和模型拟合结果有一定偏差.

图4 各年龄组每日累计确诊住院数.红点表示实际数据,蓝线表示模型预测均值,灰色阴影代表95%的置信区间Fig.4.The cumulative number of confirmed cases per day in each age group.The red dots represent the actual data,the blue line represents the solution of model 1,and the shaded gray area represents the 95% confidence interval.

图5 各年龄组每日现有确诊住院数 H k(t) .其中蓝线表示模型的解,灰色阴影部分表示95%置信区间,红线表示峰值Fig.5.The number of confirmed hospitalized cases per day in each age group.The blue line represents the solution of the model,the shaded gray area represents the 95% confidence interval,and the red line represents the peak.

图6 (a) 各年龄组每日累计确诊住院数 (b) 各年龄组每日现有确诊住院数 H k(t) .Fig.6.(a) Total number of confirmed hospitalizations per day in each age group.(b) Each age group has the number of confirmed hospitalizations H k(t) per day.
根据拟合结果,通过比较各年龄组的累计确诊住院病例曲线(图6(a))和每日现有确诊住院曲线(图6(b)),发现儿童及青少年感染人数明显少于老年组和中青年组,呈现明显的年龄异质性; 图6(b)表明老年组每日现有确诊峰值最先到达、儿童组紧随其后、中青年组最后到达.具体各个年龄组的住院病例峰值到达时间、住院峰值、最终规模、消亡时间见表5.
表5表明每日现有确诊住院数高峰老年组(65岁及以上)于1月31日到达,儿童(0—5岁)于2月2日到达,青少年组(6—19岁)和中青年组(20—64岁)于2月3日到达.由图7(a)可以看出20—64岁年龄组每日现有确诊住院峰值占比最多,65 岁及以上年龄组次之,0—5 岁年龄组最少;各年龄层最终规模(图7(a))和高峰占比构成相似;住院病例多为中青年和老年人.该结论为针对不同的年龄人群预备和筹集相应的医疗资源提供了关键信息.通过比较表1中传播概率β1,β2,β3,β4以及各年龄组最终规模,得出青少年感染新冠肺炎风险较低,20—64岁中青年染病风险较高.结合表4和表5的数据计算各年龄层最终规模占对应年龄层人数占比,结果如图7(b)所示.不难发现,65岁及以上年龄患者占比最高,而6—19岁年龄组患者占比最低.因此,老年人群易感染新冠肺炎,该年龄组人群应该加强日常新冠肺炎预防.

表5 拟合结果分析Table 5.Analysis of fitting results.
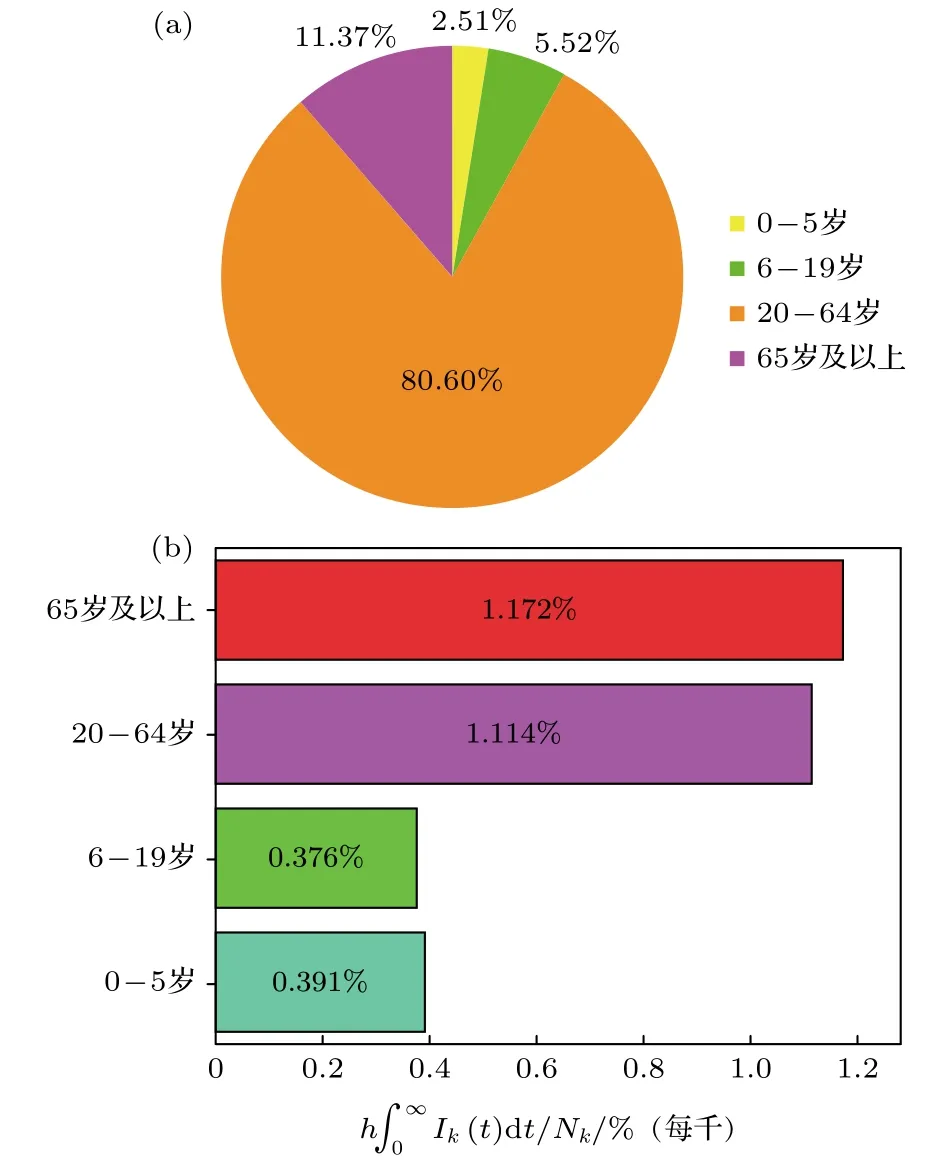
图7 (a)各年龄组最终规模占比图; (b) 各年龄层最终规模占对应年龄层人数占比图Fig.7.(a) The proportions of final size in each age group;(b) The proportion of the final size of each age group in the associated age group.
4 控制策略评估
为了评估居家隔离效果,改变接触模式,允许个体以家庭为中心,在半径为0.5 km的范围内活动,该接触模式定义为图3(b)所示的社区模式.比较两种接触模式下各年龄组感染新冠肺炎的变化.
图8表明在社区模式下,各年龄组的每日现有确诊病例数峰值及到达时间有显著差异,其中,0—5岁年龄组每日现有确诊病例数住院高峰时间将推迟2天,峰值增加9%; 6—19岁年龄组高峰到达时间推迟3天,峰值增加29%; 20—64岁年龄组高峰时间推迟近1周,峰值增加41%; 65岁及以上年龄组峰值到达时间推迟1天,峰值增加8% (表6).

表6 社区模式住院峰值到达时间及峰值Table 6.Daily peak arrival time and peak values of hospitalized cases in the community mode.
定理1表明基本再生数小于1能有效控制新冠肺炎的传播.为此,采用拉丁超立方抽样方法分析模型参数对基本再生数的影响,结果如图9(a)所示.可以看出,减小传染概率βk(k=1,2,3,4) 和提高确诊率能有效降低新冠肺炎的传播.在居家模式下,提高确诊率比其他控制策略更有效.
在居家隔离政策下,对比 1 /h天后确诊对疫情高峰的影响,分别取参数值h= 0.5,h= 1.0,h=2.0,即确诊期分别为 2 天,1 天和 0.5 天,其他参数值保持不变,结果如图9(b)所示.可以看出,如果感染者出现症状后立刻去医院检测,特别是在出现症状后半天内确诊,会明显降低住院高峰人数,同时也能缩短疫情消亡时间.说明及时就诊能有效遏制新冠肺炎的蔓延.
通过以上控制措施评估效果可以发现,实施居家隔离措施、及时隔离确诊病例并对其进行治疗是疫情防控的关键.以上所有分析都基于医疗资源充足,若考虑感染者在出现症状后不能及时得到确诊,该模型还需要进一步修改和完善.

图8 各年龄组每日确诊病例时间序列图.蓝实线表示居家模式下的每日确诊病例时间序列图,红虚线表示社区模式下每日确诊病例时间序列图Fig.8.The daily hospitalized cases for each age group over time t.The blue line represents the daily hospitalized cases in the household mode,the red dotted line represents the daily hospitalized cases in the community mode.
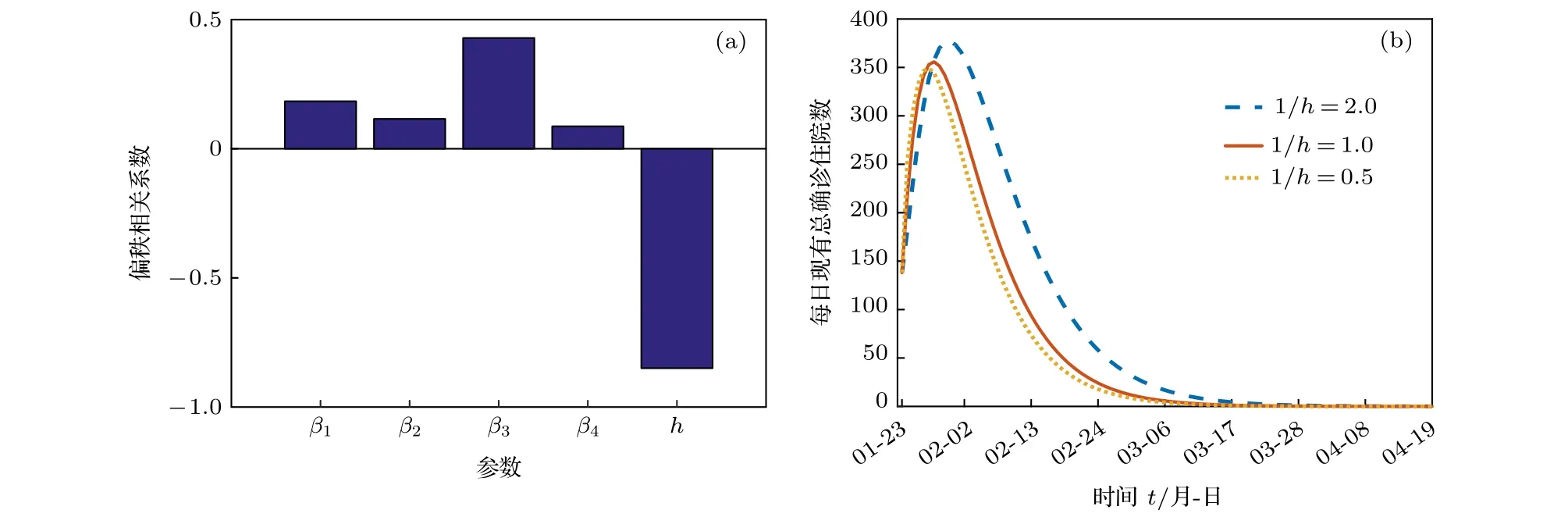
图9 (a) 参数对基本再生数 R 0 的敏感性分析; (b) 每日现有总确诊住院数 取不同确诊率时间序列图Fig.9.(a) The sensitivity analysis of model parameters to R 0 ; (b) the time series diagram of the total hospitalized cases with parameter h .
5 讨 论
本文分析了广东省944例新冠肺炎患者信息,发现广东省新冠肺炎患者各年龄患者的构成比例有显著差异.通过建立耦合不同年龄层接触模式的SEIHR模型,基于现实病例数据,利用MCMC方法,辨识模型参数,分析不同年龄段人群的新冠肺炎的传播趋势,计算出基本再生数R0= 1.2323(95% CI [1.2316,1,2329])和最终规模分别为 0—5 岁年龄组 28 例 (95% CI [23,33]),6—19 岁年龄组 61 例 (95% CI [54,69]),20—64 岁年龄组 877例 (95% CI [791,962]),65 岁及以上年龄组 125 例(95% CI [107,144]).研究发现居家模式对疫情的控制非常有效,如果政策适当放松,即社区模式下染病人数上升明显,其中20—64岁(中青年组)染病峰值比居家模式增加41%.通过分析不同年龄层感染最终规模在对应年龄层人口数的占比,发现老年人感染新冠肺炎风险较高,青少年的感染风险较低.
耦合不同年龄层人群接触模式的传染病动力学模型,本质上刻画了不同社会接触模式(物理距离)对新冠肺炎传播的影响,揭示不同年龄段人群的新冠肺炎的流行特征和规律.同时能准确捕捉不同控制策略下,人的社会行为对新冠肺炎的影响.结果表明在严格管控措施下,提高确诊和隔离率是遏制新冠肺炎传播的关键.耦合年龄结构的传染病模型为合理调派医疗资源和节约成本提供了理论依据.
图6较准确地拟合了各年龄组的确诊病累计例数,表明模型1能客观反映广东省新冠肺炎在各年龄组间的实际传播情况.与传统的均匀混合的SEIHR仓室模型相比,模型1能较准确了解新冠肺炎与年龄及物理接触距离的关系,能捕捉各个年龄组人群之间的传播动态,能较清晰地评估居家隔离对各年龄组新冠肺炎传播的影响.通过数值模拟发现,经典的均匀混合模型会高估新冠肺炎在广东省的传播,可能对及时复工复产发出误导信息(见图10).

图10 均匀混合模型与模型 (1)比较图Fig.10.The comparison diagram of uniformly mixed model and model (1).
本文虽然详细地讨论了年龄异质性及物理接触距离对新冠肺炎的影响,但模型的建立仍有许多不足.首先接触矩阵的数据由文献[14]直接获得,虽然我们采用和文献[25,26]类似的聚合方法更新接触数据,但获得的信息与实际情况有一定的偏差.受限于获得信息的不完整,目前只能依赖文献[14]提供的数据将年龄进行分层.将来如果采用更加精确的遥感设备,精确记录每天各年龄组的接触数据,进而能设计更加合理的分组方式来研究新冠肺炎的传播.其次,由于缺乏实际详细信息,模型1假设参数(除感染率外)都和年龄无关,实际上由于各年龄层个体体质不同,不同年龄层的康复期略有不同,那么康复率应该是一个与年龄有关的函数.我们将对这些遗留问题进行进一步改进和完善.

