超级质子-质子对撞机中束流热屏的热-结构耦合模拟分析*
范佳锟 王洁† 高勇 游志明 王盛‡张静 胡耀程 许章炼 王斌
1) (西安交通大学,陕西省先进核能技术重点实验室&动力工程多相流国家重点实验室&陕西省先进核能工程研究中心,西安 710049)
2) (西安交通大学机械学院,西安 710049)
束流热屏(beam screen)是新一代高能粒子对撞机中的重要部件,用于将束流在管道中运行时产生的热量转移到冷却系统中,同时通过束流热屏上的排气孔将残余气体输送至冷管壁上,维持良好的真空度.然而,在转移热负载的过程中,温度变化产生的形变会影响束流热屏的结构稳定性.如何在保证束流热屏良好传热性能的情况下,尽量减小形变是优化束流热屏结构设计的关键问题之一.本文采用ANSYS软件对束流热屏模型的传热性能和力学性能进行了模拟,并优化了束流热屏结构设计,增强其传热性能和结构稳定性.对于束流热屏外屏的内表面,采用减小铜涂层厚度的方式来降低运行过程中产生的洛伦兹力.相关理论模型计算结果表明: 与厚度为 100 µm 的铜涂层工况相比,当铜涂层的厚度在 0到 100 µm 之间变化时,厚度为 75 µm的铜涂层可以使束流热屏外屏的最大形变降低70.9%,同时使束流热屏的最高温度升高1.1%.对于束流热屏内屏,采用间隔布置支撑肋片的设计方案对束流热屏的结构进行加固处理,提高束流热屏整体的结构稳定性.计算结果表明: 与未加支撑肋片的工况相比,当相邻两个支撑肋片之间的间隔为1个排气孔时,束流热屏内屏的最大形变可降低86.8%,同时使束流热屏的最高温度降低7.69%.研究成果为新一代高能粒子加速器真空系统中关键部件束流热屏的设计提供重要的理论参考.
1 背景介绍
2012年,标准模型中希格斯粒子(Higgs boson)在欧洲核子中心被发现[1],但仍然存在着夸克-轻子对称性、电荷量化、基本粒子数量以及暗物质等标准模型所不能解释的现象[2-4].因此,探究超越标准模型的“新物理”成为粒子物理学的首要任务,也是超级质子对撞机(super proton-proton collider,SPPC)的主要目标之一[5].
高能粒子束在运行过程中产生的同步辐射等会在管道内壁产生能量沉积,造成管道温度升高,继而影响束流的稳定运行[6-9].束流热屏作为高能粒子加速器真空系统中的关键部件之一,通过将束流热屏内的热载荷转移到冷却管道内,维持超导磁铁运行所需的工作温度[10,11].同步辐射轰击在束流热屏内壁会释放出大量气体,因此,束流热屏上必须存在贯通的排气孔,使同步辐射致解吸的气体分子可以从中逸出,并且凝结在冷管道内壁上[12,13].
束流运行过程中产生的温度场变化会在束流热屏结构中产生位移和应变.同时,考虑到超导失超的情况[14,15],在进行结构分析时需要考虑洛伦兹力的因素,进行热-结构耦合分析.因此,本文采用ANSYS软件对束流热屏设计方案进行改进和优化,以增强其结构性能和传热性能,从而保证束流运行的稳定性.
2 模型与方法
2.1 模型介绍
束流热屏模型[16-19]的结构和尺寸如图1所示.在本文的模拟中,SPPC的束流热屏主体材料选择316LN不锈钢[20-23].其中,不锈钢表面镀了一层铜涂层,铜材料选择剩余电导率RRR(residual conductivity ratio)为100的高电导率无氧铜[17].当温度为20 K时,不锈钢和无氧铜的物性参数如表1所列[20-26].
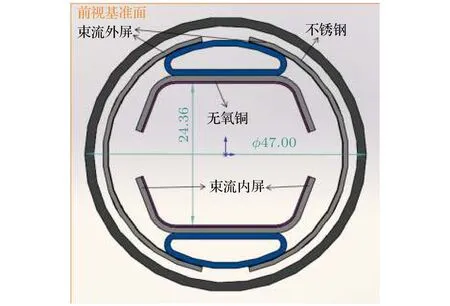
图1 束流热屏模型的结构和尺寸Fig.1.Structure and size of beam screen model.
2.2 热负载与洛伦兹力
2.2.1 热负载
束流热屏上的热负载主要有三个来源,分别是同步辐射、镜像电流和电子云产生的热负载[6,12].在SPPC中,辐射沿水平面与轨道相切地发射,是束流热屏上热负载的主要来源[10,11].管壁镜像电流产生的热负载与束流热屏材料的电导率相关[6].本文采用在束流热屏内壁上镀一层高电导率无氧铜的方法来降低镜像电流产生的热负载.束流与残余气体相互作用引起的相关效应最终导致电子云的形成,在束流热屏内壁产生热负载[27,28].综合考虑三种热负载,SPPC的束流在运行过程中产生的总热负载为17.08 W/m[16].
2.2.2 洛伦兹力
磁场引起的洛伦兹力作用在束流热屏上引起形变,使其在水平方向上张紧,而在垂直方向上收缩.超导磁铁失超时的磁场会在束流热屏内部感应出涡流[14,15],涡流的强度由感生电场的强度以及材料的电阻率决定.涡流在磁场结构内部沿着闭合回路运动,在磁场的作用下产生洛伦兹力,作用在束流热屏结构上.对SPPC的束流热屏而言,超导磁铁失超过程中的最大洛伦兹力为
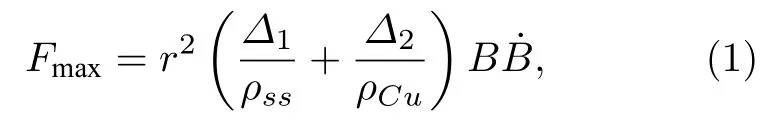
其中r为束流热屏结构的半径;Δ1为316 LN不锈钢的厚度;Δ2为无氧铜的厚度;ρss为 316 LN 不锈钢的电阻率;ρCu为无氧铜的电阻率;B为磁感应强度,12 T;为磁感应强度的变化率,63 T /s .对于SPPC而言,束流热屏内屏边缘处和外屏中心处的洛伦兹力最大值分别为23.6 N/mm和15.2 N/mm.
2.3 网格独立性分析
本文研究的束流热屏模型采用ANSYS meshing 进行网格划分.在冷却剂管道温度为 80 K,束流运行过程中产生的总的热负载为17.08 W/m时,对束流热屏模型进行网格独立性分析.根据划分网格几何尺寸的不同,得到如图2所示的五种网格数目的最高温度计算结果.由图2可知,在网格数大于248956时,束流热屏的最高温度变化小于0.01 K.考虑到计算精度和效率,束流热屏所用的网格数为248956.

表1 温度为 80 K 时,无氧铜和 316LN 不锈钢的材料属性Table 1.Material properties of oxygen-free copper and 316LN stainless steel at 80 K.
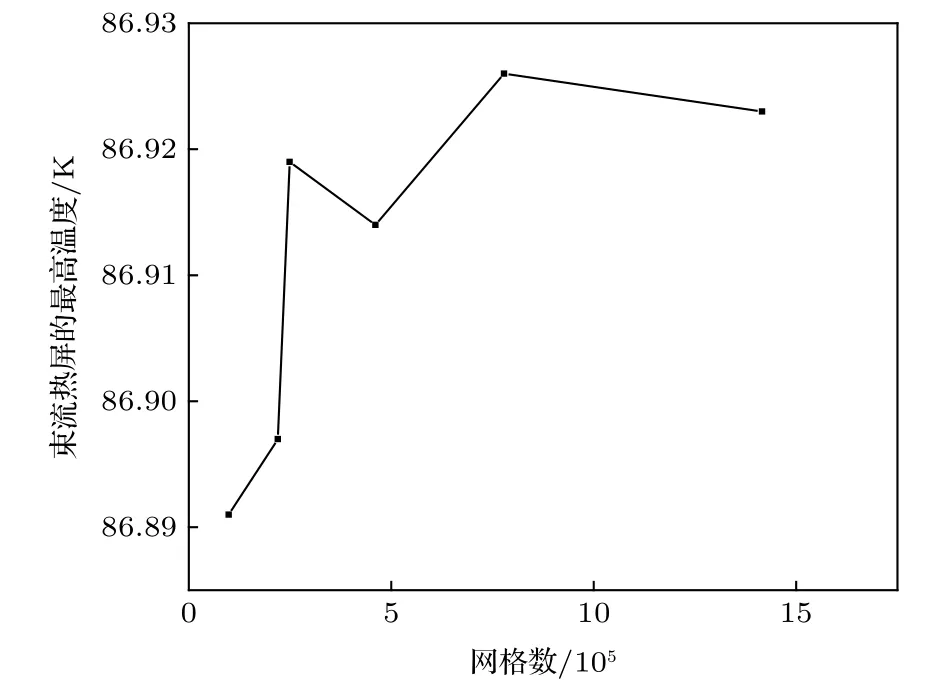
图2 五种网格数目的束流热屏最高温度计算结果Fig.2.The calculation result of the maximum temperature of beam screen with five kinds of the grids.
2.4 可靠性分析
为了验证所采用的束流热屏模型以及网格划分方式的正确性,使用COMSOL仿真软件在相同的工况下对同一模型进行验证.在冷却剂管道温度为 80 K,排气孔开口面积比为 6% 时,COMSOL的模拟结果为83.756 K,ANSYS在相同条件下的模拟结果为 83.613 K,误差为 0.17%,在可接受的范围内,因此可以验证本文所采用的束流热屏模型以及网格划分方式的正确性.
3 热-结构耦合模拟
在80 K的工况下对束流热屏模型进行温度场模拟,所涉及关键参数如表1 所列,316 LN 不锈钢和无氧铜的导热系数分别为 8.12 W m—1K—1和 540 W m—1K—1,将得到的温度场模拟结果作为载荷施加到静力学结构分析模型上,所涉及关键参数如表1所列.根据实际情况,将所有接触面的接触关系定义为Bonded,对冷管壁外表面施加固定约束,限制其位移,对束流热屏两端横截面施加无摩擦约束,限制其法向位移,允许进行径向位移,其他表面不施加约束.
3.1 无洛伦兹力情况下的热-结构耦合模拟结果
在无洛伦兹力情况下,当冷却管道内温度为80 K,排气孔开口面积比为6%时,对束流热屏的形变量进行分析.通过如图3(a)所示的四个路径,对束流热屏上的形变量进行分析.在图3(b)中,束流热屏距离为0处是指束流热屏内屏与上冷却管道相切处,其他距离是指以相切处为起点,沿着路径1上某一点与相切处的距离.束流热屏内屏处形变量沿着路径1的变化如图3(b)所示.
由计算结果可以得到: 沿着路径1,束流热屏内屏形变量沿着路径1基本呈线性变化,在接近底部的位置形变仅为0.006 mm,在顶端则达到了最大形变量 0.031 mm,总体形变量较小,相对最大形变量为 2.3%.在图3(c)中,束流热屏距离为0处是指束流热屏外屏最左端,其他距离是指以最左端为起点,路径3上某一点与起点间的距离.束流热屏外屏的形变量随距离的变化如图3(c)所示,形变呈波状分布,变化趋势与排气孔位置的分布相关.束流热屏的向外形变位于排气孔之间,最大形变量为0.074 mm; 束流热屏的向内形变位于相邻排气孔的间隙处,最大形变量为0.065 mm.
3.2 有洛伦兹力情况下的热-结构耦合模拟结果
在束流热屏内屏边缘处以及束流热屏外屏中心处分别施加大小为23.6和15.2 N/mm的洛伦兹力,水平指向束流热屏外侧.图4为冷却管道内温度为80 K,排气孔开口面积比为6%的工况下,施加了洛伦兹力的热-结构耦合模拟结果.可以看到形变的最大值出现在束流热屏外屏受同步辐射处,最大形变量为0.428 mm.总形变可分解为沿X,Y,Z三个方向的定向形变,分别如图4(b),图4(c)和图4(d)所示.
图4(b)为X方向上的形变分布云图,其中红色代表和X方向同向的形变,蓝色代表和X方向反向的形变.可以看到X方向上的形变集中在束流热屏外屏中心处和内屏边缘处,分别向两侧发生形变,最大形变量为 0.416 mm.束流热屏内屏边缘处的X方向上的形变方向和束流热屏外屏形变方向一致,指向束流热屏外侧.这是由于洛伦兹力产生的形变大于温度引起的形变引起的,从而使束流热屏内屏的形变方向变为相反方向.在束流热屏的其他位置X方向上的形变量很小,束流热屏X方向上总体的形变呈现出向两侧扩张的趋势.

图3 不同路径和束流热屏形变随不同路径的变化 (a) 路径1、路径2、路径3和路径4的示意图; (b) 束流热屏内屏形变量沿着路径1的变化; (c) 束流热屏外屏形变量沿着路径3的变化.Fig.3.Different paths and variations with distance along paths in beam screen.(a) Schematic of paths 1,2,3 and 4; (b) variations of the inner screen with distance along path 1 in beam screen; (c) variations of the outer screen with distance along path 3 in beam screen.
图4(c)为Y方向上的形变分布云图,与X方向上的形变分布云图相似,红色和蓝色分别代表和Y方向同向和反向的形变.可以看到束流热屏在Y方向上的形变集中在冷却剂管道周围,束流热屏上部的形变量略大于下部的形变量,最大形变量为 0.273 mm.因此,重力加剧了束流热屏上部的形变,束流热屏下部的形变正好相反,束流热屏两侧对下部进行拉扯引起的形变方向与重力作用方向相反.因此,重力作用在一定程度上缓解了束流热屏下部的形变.在束流热屏其他位置Y方向上的形变很少,束流热屏Y方向上总体的形变呈现向内部压缩的趋势.
图4(d)为Z方向上的形变分布云图,形变集中在排气孔两侧,呈挤压排气孔的趋势.X,Y和Z方向上的形变量最大值分别为0.416,0.273和0.014 mm,形变主要出现在X和Y方向上.出现这种情况的原因是: 排气孔周围温度分布平均且较低,并且上下两侧有束流热屏其他部分结构上的支撑来保持排气孔部分的结构稳定性.
有洛伦兹力的情况下,束流热屏内屏形变量沿着路径1的变化如图5(a)所示,形变量的范围是在0.2—0.387 mm之间.相比于无洛伦兹力作用下的最大形变量(0.031 mm),有洛伦兹力存在情况下的最大形变量提高了近12倍.除了数值上的变化,有无洛伦兹力两种工况下,束流热屏内屏处的形变另一个区别在于两者的方向是相反的.因此,在洛伦兹力作用前后,束流热屏内屏顶端形变变化最大,由指向内侧的最大形变量0.031 mm变为指向外侧的 0.387 mm,形变变化量为 0.418 mm,相对最大形变量为29.7%.
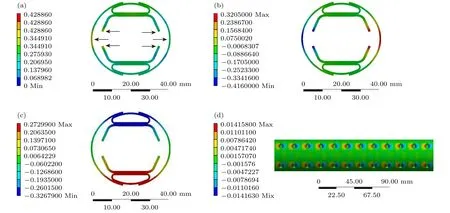
图4 有洛伦兹力情况下的热-结构耦合模拟结果 (a) 总体形变分布; (b) X 方向上的形变分布云图; (c) Y 方向上的形变分布云图; (d) Z 方向上的形变分布云图Fig.4.Simulation results of thermal-structure coupling with Lorentz force: (a) Overall deformation distribution; (b) cloud map of deformation distributions in X direction; (c) cloud map of deformation distributions in Y direction; (d) cloud map of deformation distributions in Z direction.
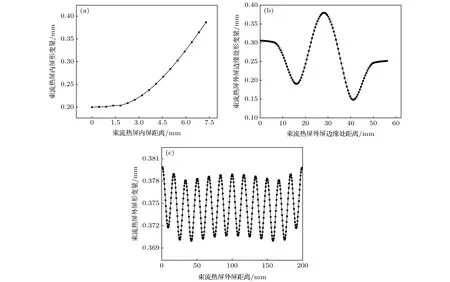
图5 束流热屏形变随不同路径的变化 (a) 束流热屏内屏处形变量沿着路径1的变化; (b) 束流热屏外屏边缘处沿着路径2的形变量; (c) 束流热屏外屏形变量沿着路径3的变化Fig.5.Variations with distance along paths in beam screen: (a) Variations of the inner screen along path 1 in beam screen; (b) variations of the edge of outer screen along path 2 in beam screen; (c) variations of the outer screen along path 3 in beam screen.
束流热屏外屏边缘处形变量沿着路径2的变化如图5(b)所示.路径2的起点为束流热屏外屏与上冷却管道的相切点.在0—7 mm处即接近束流热屏顶部冷却剂管道处,Y方向上的形变占主要地位.随着位置向下移动,在 7—18 mm 处即排气孔处的形变主要由X和Y方向上的形变构成,两者的形变数值较小.因此,在排气孔处的形变小于排气孔两侧的形变,在18—28 mm处即束流热屏外屏中心上侧,X方向上的形变占主要地位,并且在中心点处达到了最大值.束流热屏外屏下侧部分变化趋势与上侧总体呈对称分布,其中数值上不对称是由于重力作用的影响.
有洛伦兹力的情况下,束流热屏外屏形变量沿着路径3的变化如图5(c)所示,其外屏形变量变化趋势与无洛伦兹力的情况下的变化趋势相似,但最大形变量由 0.074 mm 增加到了 0.379 mm,最小形变量则由0.065 mm增加到了0.370 mm.
4 束流热屏的结构稳定性强化
在无洛伦兹力作用的情况下,束流热屏的形变主要出现在束流热屏内屏处,最大形变量为0.031 mm,方向指向束流热屏内侧; 在有洛伦兹力作用的情况下,束流热屏的形变主要出现在束流热屏内屏及束流热屏外屏中心处,最大形变量为 0.387 mm,方向指向束流热屏外侧.束流热屏内屏和束流热屏外屏的相对最大形变量分别为29.7%和42.1%.因此,需要考虑对束流热屏进行结构上的优化和改进,增强其机械性能,从而使束流稳定运行.
4.1 束流热屏外屏的结构稳定性强化
保持束流热屏的结构稳定性有三个方面: 一是改变材料,采用强度更大的材料作为束流热屏的主体材料; 二是对形变较大处进行加固处理,如增加厚度等; 三是降低束流热屏上的洛伦兹力,从而减小形变.本文对束流热屏外屏的结构稳定性强化主要基于后面两个方面.对于束流热屏外屏,其与外部冷管壁之间的距离仅为1 mm,采用加固处理的方式有局限性且效果不明显.因此,通过降低运行过程中产生的洛伦兹力来对束流热屏外屏进行结构稳定性强化.
同等条件下,无氧铜内洛伦兹力远大于不锈钢内的洛伦兹力.因此,降低铜涂层的厚度是降低洛伦兹力的有效方式,但铜涂层厚度的增加有利于增强传热.在80 K的温度下,铜和不锈钢的导热系数分别为 540 W/mK 和 8.12 W/mK,两者相差近67倍.因此,需要分析不同厚度的铜涂层对传热性能的影响.对于束流热屏内屏,在没有洛伦兹力作用的情况下,也存在着一定的形变.单纯地降低洛伦兹力不能很好地保持其结构稳定性,考虑到束流热屏内屏与束流热屏外屏之间空间较大,可以采用加固处理的方式增加其机械强度.
4.1.1 不同铜涂层厚度对束流热屏传热性能和结构稳定性的影响
在冷却管道内温度为80 K,排气孔开口面积比为6%的情况下,分别对铜涂层厚度为0,25,50,75和100 µm的束流热屏模型进行温度场模拟分析.由图6 可知,与 100 µm 厚铜涂层工况相比,铜涂层厚度为 0,25,50 和 75 µm 的束流热屏模型最高温度分别增加了 31.6%,7.9%,3.2% 和 1.1%.铜涂层的存在对束流热屏的传热能力有着很大的影响,但温度分布趋势则基本相同.
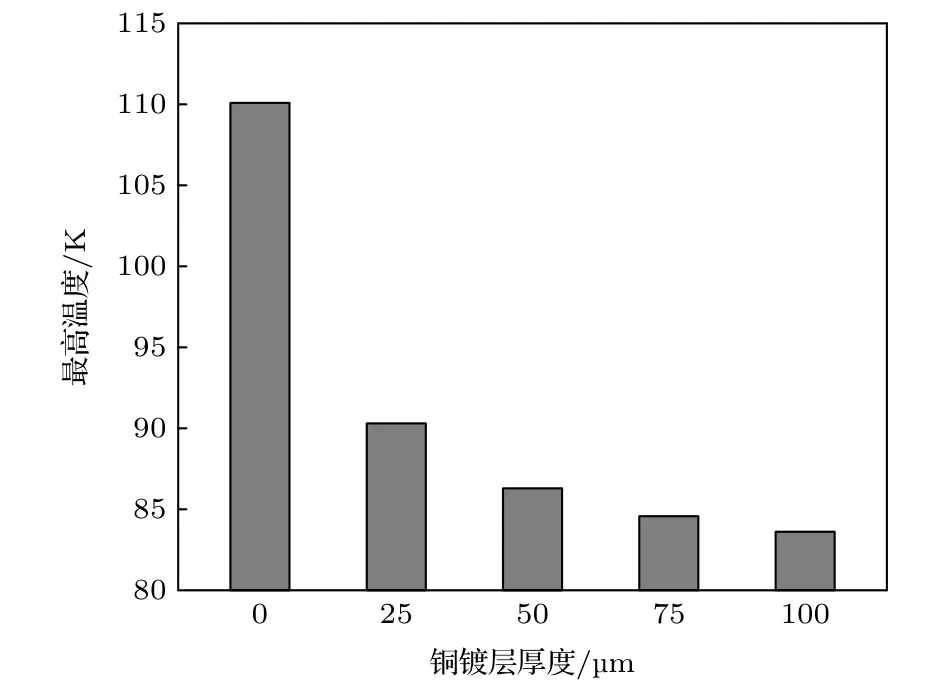
图6 不同铜涂层厚度下的束流热屏模型最高温度Fig.6.Maximum temperature of beam screen model under different copper plating thickness.
由于铜涂层厚度发生改变,作用在束流热屏外屏上的洛伦兹力也发生了改变.根据(1)式,铜涂层厚度为 0,25,50,75 和 100 µm 时,洛伦兹力分别为 0.58,4.23,7.88,11.53 和 15.18 N/mm.在冷却管道内温度为80 K,排气孔开口面积比为6%的情况下,分别对上述五种束流热屏模型进行热-结构耦合分析.由图7 可知,相比于 100 µm 厚铜涂层的束流热屏外屏最大形变量,铜涂层厚度为0,25,50和75 µm的束流热屏外屏最大形变量分别为 0.059,0.062,0.087,0.11 和 0.379 mm,即分别降低了 84.4%,83.6%,77.0% 和 70.9%.当铜涂层厚度为100 µm时,形变量最大且远高于其余四种厚度的束流热屏外屏形变量,其余四种厚度的束流热屏外屏形变量在0.059—0.11 mm之间.综合考虑传热性能和结构稳定性的因素,选择使用厚度为75 µm的铜涂层比较合适.

图7 不同铜涂层厚度下的束流热屏外屏最大形变量Fig.7.Maximum deformation of beam screen outside screen under different copper coating thickness.
4.2 束流热屏内屏的结构稳定性强化
束流热屏内外屏之间的空隙在束流运行过程中起到了气体分子逸散通道的作用.因此,采用在束流热屏内屏外侧增加支撑肋片的方式来对束流热屏内屏进行结构稳定性强化,如图8(a)所示.
本文选取以下五种不同的支撑肋片分布方式,即每两个支撑肋片之间分别间隔1个、2个、3个、4个和5个排气孔.图8(b)和图8(c)分别是相邻支撑肋片间隔1个排气孔时的支撑肋片分布以及束流热屏模型温度分布图,其中蓝色部分为支撑肋片.接下来将分析不同的支撑肋片分布对束流热屏传热性能和结构稳定性的影响.
4.2.1 支撑肋片结构对束流热屏传热性能的影响
在冷却剂管道温度为80 K的情况下,分别对五种束流热屏模型进行热-结构耦合分析,计算结果如图9所示.在没有支撑肋片存在的情况下,束流热屏的最高温度为83.613 K.支撑肋片间隔排气孔数量分别为1个、2个、3个、4个和5个的束流热屏模型的最高温度分别为83.335,83.388,83.542,83.577 和 83.588 K,这五种工况下的最高温度变化量相比于无支撑肋片存在的束流热屏模型的最高温度变化量分别降低了7.69%,6.22%,1.96%,0.99% 和 0.69%.
4.2.2 不同支撑肋片分布对束流热屏内屏结构稳定性的影响
在冷却管道内温度为80 K,排气孔开口面积比为 6%,洛伦兹力分别为 23.62和 15.18 N/mm的工况下,对五种不同支撑肋片分布的束流热屏模型进行热-结构耦合分析.图10为支撑肋片间隔排气孔数量分别为0个、1个、2个、3个、4个和5个的束流热屏内屏边缘处沿着路径4的形变分布.
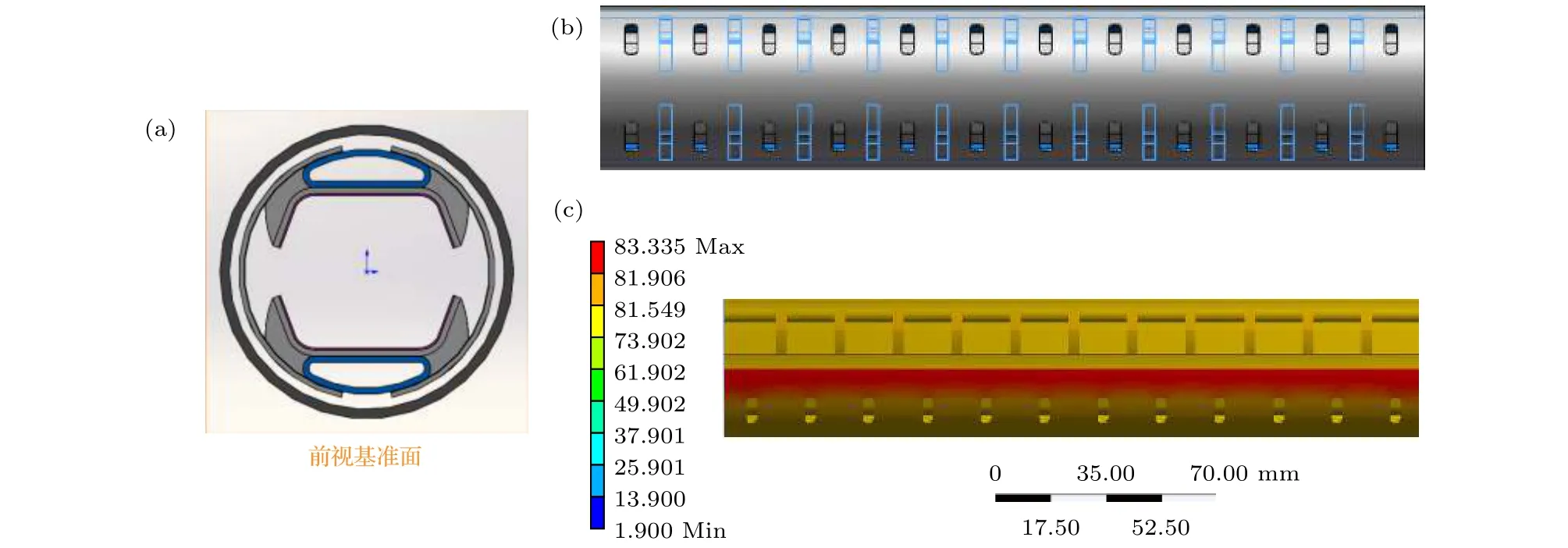
图8 (a)增加支撑肋片的束流热屏模型; (b)相邻支撑肋片间隔排气孔数量为1个时的支撑肋片分布; (c)相邻支撑肋片间隔排气孔数量为1个时束流热屏模型的温度分布图Fig.8.(a) Beam screen model with added support ribs; (b) distributions of support fins when the number of exhaust holes between adjacent support fins is one; (c) temperature distribution diagram of the beam screen model when the number of exhaust holes between adjacent support fins is one.
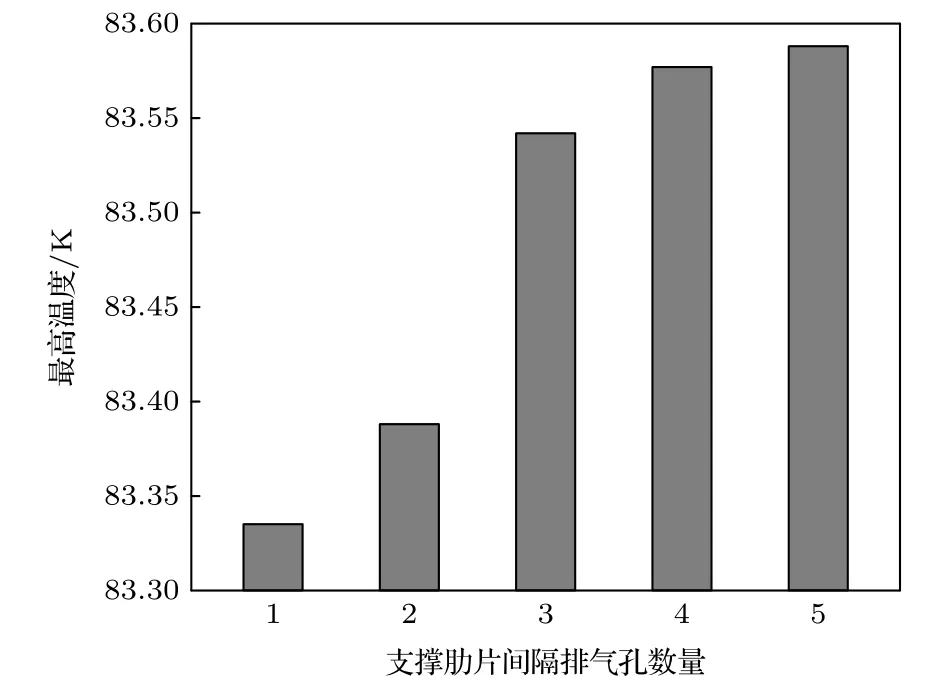
图9 不同支撑肋片分布下的束流热屏最高温度Fig.9.Maximum temperature of beam screen under different supporting ribs distribution.

图10 6种不同支撑肋片束流热屏内屏边缘处沿着路径4的形变分布Fig.10.Deformation distributions along path 4 at the edge of inner screen of six beam screens with different number of support ribs.
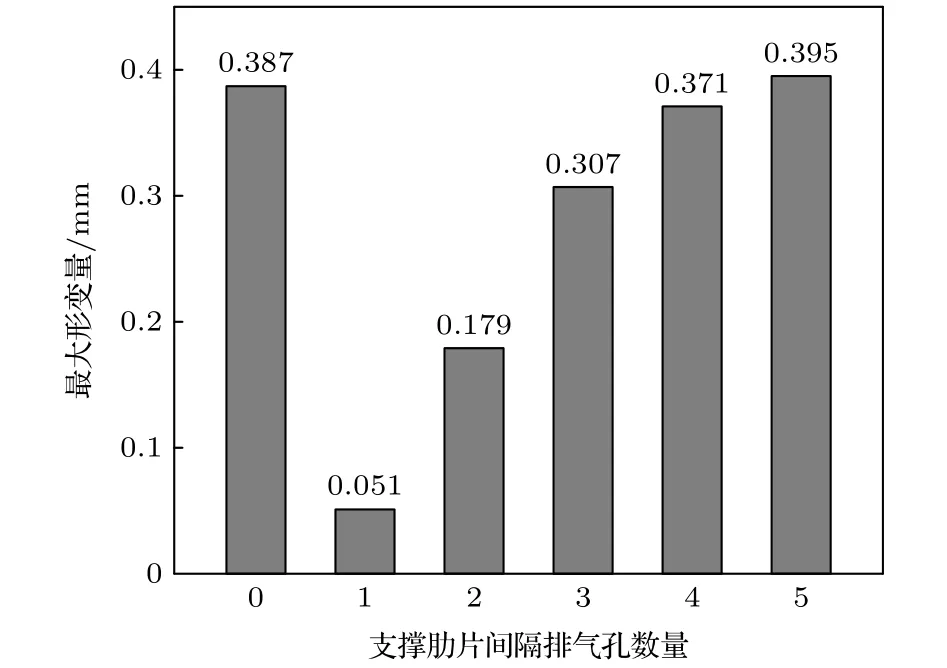
图11 六种束流热屏的内屏边缘处最大形变量Fig.11.Maximum deformation at the edge of the inner screen of six beam screens.
由图11可知,无支撑肋片时,束流热屏的内屏边缘处最大形变量为0.387 mm,支撑肋片间隔排气孔数量分别为1个、2个、3个、4个和5个时的束流热屏模型最大形变量分别为0.051,0.179,0.307,0.371 和 0.395 mm.相比无支撑肋片的束流热屏模型的最大形变量,这五种工况的最大形变量分别降低了 86.8%,53.7%,20.6%,4.1% 和 2%.
由图10和图11可知,当束流热屏模型的支撑肋片间隔排气孔数量为1个时,束流热屏内屏的形变量最低且远低于其他五种模型的束流热屏内屏形变量,而且分布更加均匀.因此,选择支撑肋片间隔排气孔数量为1个的支撑肋片分布模式来增强束流热屏内屏的结构稳定性.
5 结 论
本文基于ANSYS 软件,针对束流热屏冷却管道内温度为80 K,排气孔开口面积比为6%的工况,对束流热屏的传热性能和结构稳定性进行了综合分析.在温度场和洛伦兹力共同作用下,束流热屏X方向上最大形变量为0.416 mm.Y方向上的最大形变量为0.273 mm.Z方向上的形变量最大值仅为0.014 mm.为了增强束流热屏的的结构稳定性,采用减小铜涂层厚度的方式来降低运行过程中产生的洛伦兹力,同时采用加固处理的方式来增加束流热屏内屏的结构稳定性.铜涂层厚度分别为 0,25,50,75 和 100 µm 时,最高温度分别为110.09,90.302,86.295,84.569 和 83.613 K,铜涂层的厚度对束流热屏传热性能有着很大的影响,相应的最大形变量分别为 0.059,0.062,0.087,0.11和0.379 mm.铜涂层厚度的变化带来的洛伦兹力的变化造成了束流热屏外屏最大形变量的变化.综合考虑传热性能和结构稳定性的因素,选择使用75 µm的铜涂层.在没有支撑肋片存在的情况下,束流热屏的最高温度为83.613 K.支撑肋片间隔排气孔数量分别为1个、2个、3个、4个和5个的束流热屏模型的最高温度变化量相比于无支撑肋片存在的束流热屏模型的最高温度变化量分别降低了 7.69%,6.22%,1.96%,0.99% 和 0.69%.当束流热屏模型的支撑肋片间隔排气孔数量为1个时,束流热屏内屏的形变量最低且远低于其他五种模型的束流热屏内屏形变量.因此,合理设置支撑肋片能够增强束流热屏的传热能力和结构稳定性.

