计算机算法技术在静力触探试验中的层位划分应用

鲁国浩，刘龙飞

（中建三局工程设计有限公司 武汉430070）

0 引言

在岩土工程勘察中，对地下土层进行划分，有助于查明地下土层构造及变化情况。目前，在实际勘察工作中，主要采用钻探及原位测试技术来了解地下土层的变化情况，静力触探试验作为一种原位测试的方式，具有数据连续，对土层扰动小，深度精确等优点，适用于软土、粘性土、粉土、砂类土及含有少量碎石的土层［1］，相较于钻探而言，此方法在层位划分领域具有更加明显的优势。

静力触探技术在我国发展较为久远，早在20世纪30 年代就出现机械式的静力触探仪，1954 年，陈宗基教授利用该技术成功在黄土地区进行了试验研究［2］；1964 年，我国首创电测静力触探技术，此项原位测试技术在1966 年开始全国推广，并于20 世纪70 年代被列入国家规范和许多部门及地方规范，解决了大量的岩土原位测试问题，取得了重大的技术经济效益［3］。

在目前的工程应用中，主要使用的依然是“单桥”探头和“双桥”探头［4］，通过多年的实践积累，目前我国已经形成了针对这2种类型静力触探的相关标准和规范。但是在实际的应用过程中，由于缺乏简单实用的工具或手段，目前勘察人员在利用静力触探数据进行层位划分的时候，主要依据经验和相关的分类公式来进行土层分类，不够直观和精确，直接影响到了层位划分的效率及可靠性。

本文针对这一问题，尝试利用计算机编程的手段，在总结前人经验的基础上，归纳相关标准及规范，开发了一系列简单实用的算法，为利用静力触探试验进行层位划分提供参考。

1 研究方法及应用

1.1 单桥静力触探试验分析算法

1.1.1 算法原理

由于单桥静力触探仪只能获得比贯入阻力Ps这一个类型的数据，只依靠这一个参数并不能确定土的具体类型，需要结合周边的钻探情况来综合分析判定不同深度土的具体类型，它仅适用于城市、工矿区等对当地地层已有概略了解的地方［5］。目前，湖北地区已经建立了比贯入阻力Ps同黏性土塑性的关系，如果利用钻孔和静力触探的数据综合分析，能够判定某一深度土层为黏性土，就可以利用Ps与黏性土塑性的关系，对黏性土层进行进一步的划分。

依据湖北省地方标准《建筑地基基础技术规范：DB 42/242-2014》［6］的说明，武汉地区室内试验的液性指数与比贯入阻力具有以下统计关系：

式中：IL为液性指数；Ps为比贯入阻力（kPa）。

根据液性指数同黏性土状态之间的关系（见表1），利用式⑴可以确定黏性土状态与Ps的对应关系［6］。

表1 黏性土状态与Ps关系Tab.1 Relationship between the State of Cohesive Soil and Ps

根据上述关系，结合实际工作经验，编写相应算法，在输出Ps值，绘制静探曲线图的同时，绘制相应的比贯入阻力临界线，将临界线与静探曲线置于同一图件中，可以直观地判定黏性土的塑性状态及具体分布。

1.1.2 实际应用

在湖北省孝感市某地区（靠近武汉）进行岩土工程详细勘察，根据已有的钻探资料，发现该勘察区域存在较厚的黏性土层，利用单桥静力触探分析算法，结合钻孔试验结果，对本区域静探孔进行层位划分。选取部分静探数据进行分析说明。

如图1所示，J64和J60为本区域的2个静探孔，根据周边的钻孔试验结果，确定地下约9 m 范围深度内的土层为黏性土，按照图1，可以将这部分黏性土按照可塑性分成3 个部分，具体划分情况如表2 所示，由表2可知，这一剖面的地层分布较为均匀，地层起伏变化不大。

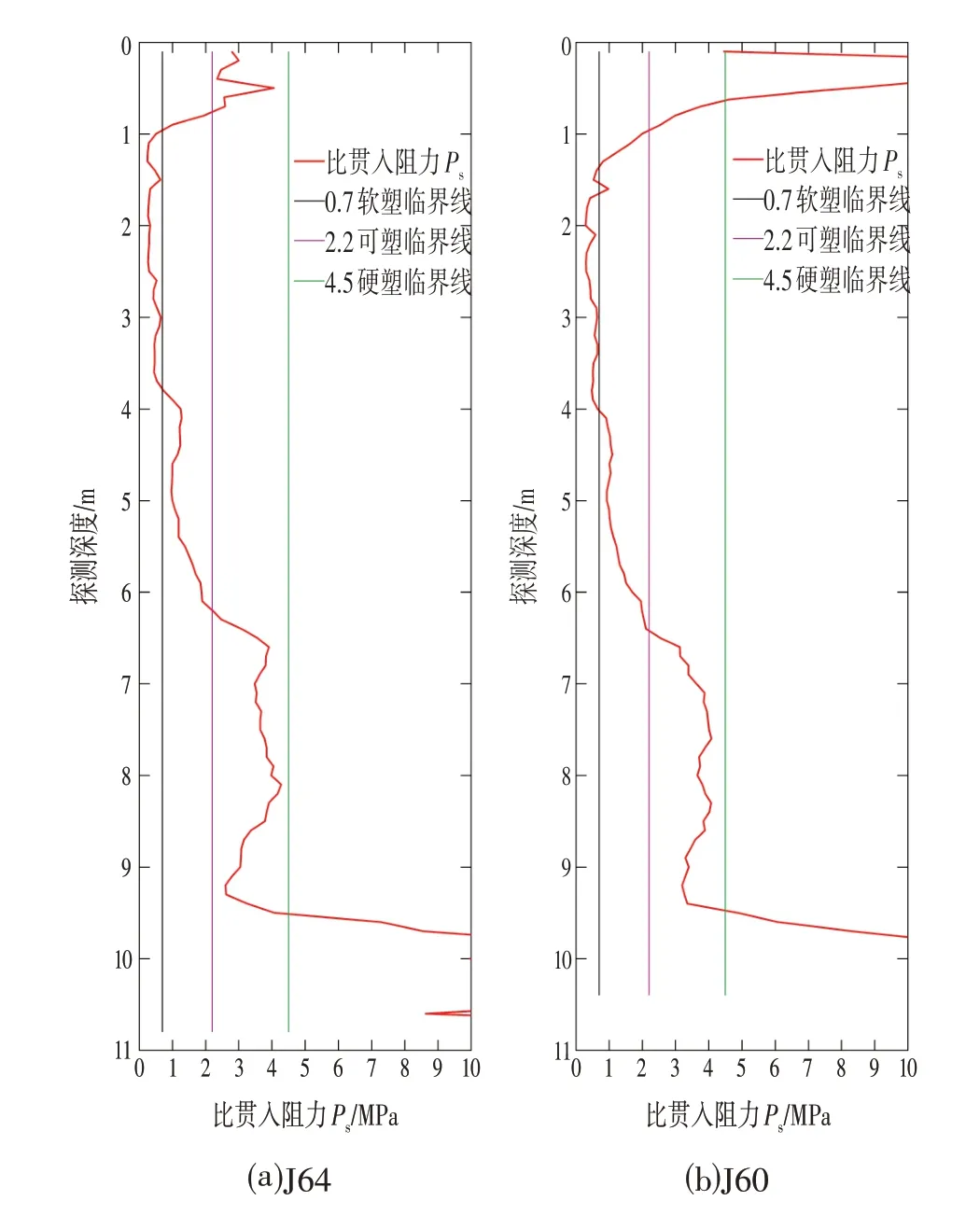
图1 单桥静探分析对比Fig.1 Comparison of Single Bridge CPT Analysis

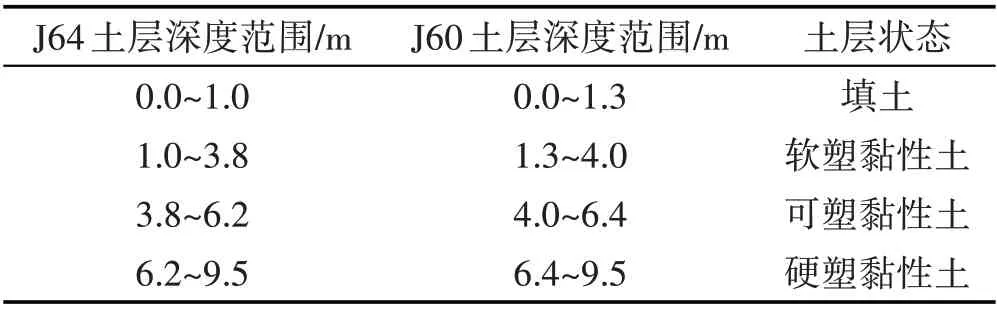
表2 静探孔土层分类Tab.2 Soil Layer Classification of CPT Hole

为了验证算法的可靠性，将在两静探孔原位置进行钻探而获得的土工样本进行试验，试验结果如表3所示。

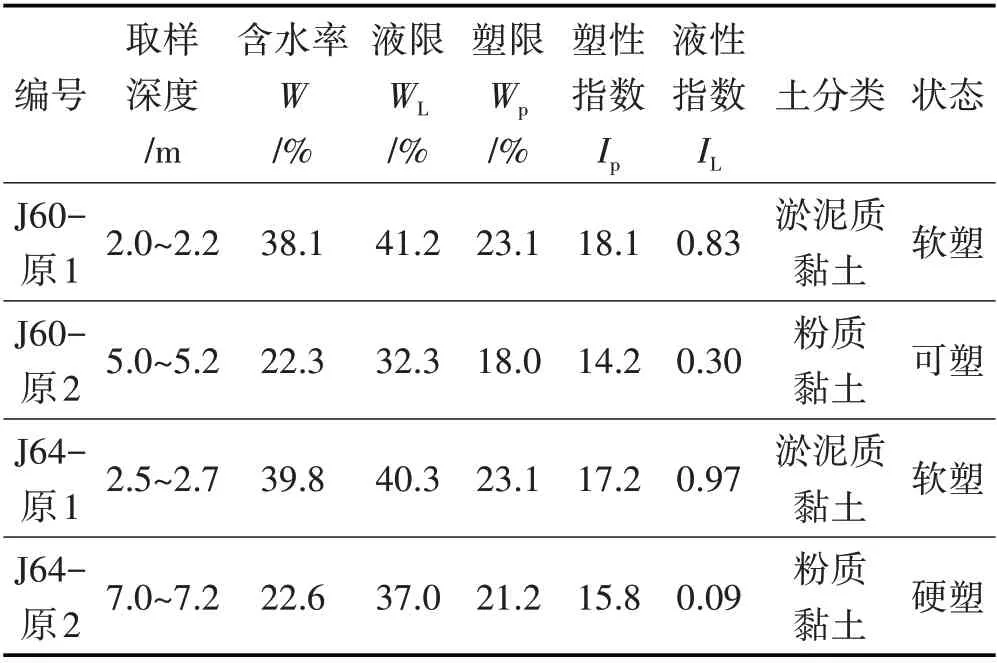
表3 土工试验表1Tab.3 Geotechnical Test Table 1

对比表3 与图1，不同深度处的黏性土状态结果同静力触探试验的分析结果基本吻合，也验证了该算法的可靠性。

通过单桥静力触探试验分析算法，可以直接将比贯入阻力Ps的具体数值同黏性土的状态连系起来，虽然利用手绘或者其他方法也可以建立这种连系，但是利用算法运算实现这一目标更加的简单高效，一目了然，只需要输入确定的孔号，就可以自动生成相应的对比图，灵活方便。

以上基于单桥静力触探的分析算法是根据湖北省的相关规范开发所得，目前适用范围有限，后期需要对更广泛的土工试验数据和单桥静力触探试验数据进行进一步的对比分析，完善算法，扩大适用范围。

1.2 双桥静力触探试验分析算法

单桥静力触探数据形式单一，应用范围有限，双桥静力触探可同时获得锥尖阻力qc和侧壁摩阻力fs两个参数，当触探过程中遇到相同的qc，可以利用fs的差异性来区分土类，反之，fs若相同，也可根据qc的差异区分土类，因为不同土的qc和fs值不可能都相同，因而可利用qc和fs/qc（摩阻比）2 个指标来区分土层类别［7］，所以双桥静力触探比单桥静力触探精度更高，且触探方式与国际相统一［8］。

1.2.1 算法原理

经过多年的实践和统计分析，目前已经有多种利用双桥静探划分土层的经验公式和分类图表。本文利用文献［8］中多年来在静力触探实践中总结的经验公式，使用计算机编程的方法，开发出一套基于双桥静探试验的简便直观的分层辅助算法。

如图2 所示，可以利用端阻qc和摩阻比Rf的数量关系对土层进行划分［9］。

图2 双桥静力触探土层分类Fig.2 Soil Classification of Double Bridge CPT

根据此分类图建立的算法流程如图3所示。按照图3 流程设计算法，读取地下相应的深度Xr和代表土类别的数值C，绘制相应的图件，即可判定任意静探孔在不同深度处的土层类别。

图3 双桥静探分析算法流程Fig.3 Flow Chart of Double Bridge CPT Algorithm

1.2.2 实际应用

在山东省东明县某地区进行岩土工程详细勘察，采用双桥静力触探试验对地下土层进行分类识别。根据钻孔试验得到的信息，该地区以粉土和粉砂为主，局部夹软塑的粉质黏土，但是在实际的钻探过程中，由于施工技术的限制，现场勘察人员很难有效区分粉土和粉砂在地下的准确变化情况，需要借助双桥静力触探试验数据来进一步划分土层。此处选取部分静探孔试验数据进行说明。

如图4 所示，SJ219 与SJ220 为同一剖面的两个双桥静力触探孔，从图4中可以看出，分层线C中的每一个点*都包含着该深度处土的类别信息，根据每一个点*的横坐标的数值，即可判定土的类别。点*的横坐标的数值为5、4、3、2、1分别代表的土层为砂土、粉土、粉质粘土、粘土、软土。

图4 双桥静探分析对比Fig.4 Comparison of Double Bridge CPT Analysis

通过这种对应关系，根据静探对比分析图的判定，结合钻孔试验的信息及现场地质条件的现状，就可以有效地把该剖面中的2 个静探孔进行层位划分，以SJ219 静探孔为例，可将该静探孔的层位分成7 部分，具体如表4所示。

表4 静探孔SJ219层位划分Tab.4 Soil Layer Division of CPT Hole SJ219

表5 土工试验表2Tab.5 Geotechnical Test Table 2

表6 土工试验表3Tab.6 Geotechnical Test Table 3

同理，也可以按照相同的思路将静探孔SJ220 划分成7 层，最终对比分析发现，该剖面土层较为均匀，土层性质随深度变化较大。

为了验证算法的可靠性，将在静探孔SJ219 原位置进行钻探而获得的土工样本进行试验，试验结果如表5、表6所示。

对比表5、表6 与图4，不同深度处的土类别结果同双桥静力触探试验的分析结果基本吻合，这证明了该算法的可靠性。

利用双桥静力触探分析算法，可以对任意剖面中的任意静探孔进行分析对比，且不受剖面中静探孔数量的限制，只需要输入静探孔孔号即可得到相应的分析对比图，比起利用Excel 数据表格等常规方法来分析，该方法操作简便，结果直观，具有对比意义，同时也更加灵活，自动化程度高，比起利用经验来直接分析判定，该方法更加的准确可靠。

1.3 全区域双桥静探综合分析辅助算法

1.3.1 算法原理

双桥静力触探试验分析算法利用摩阻比Rf和端阻qc之间的关系，可以较直观准确地判定任意静探孔的土层变化情况，考虑的是对有限个静探孔或者有限个剖面的分析对比。而在实际的勘察工作中，静探孔的数量往往高达数百个，需要首先综合全区域所有的静探孔和钻孔的数据信息，给出勘察区域的标准地层表，然后再对每一个具体的孔位进行进一步的分析判定，同时还要考虑到实际地形的起伏变化情况，此时只能分析有限个静探孔的双桥静力触探试验分析算法就无能为力了，同时该算法也忽略了地形起伏的影响，不能体现整个勘察区域地层的主要变化情况。

针对以上问题，为了更好地掌握勘察全区域地层的变化情况，给勘察区域标准地层表的确定提供有效的辅助手段，尝试着开发了一套全区域双桥静探综合分析辅助算法。该算法通过读取勘察区域所有静力触探孔的孔号名称及地面标高，将所有的静力触探孔按照图2 的分类方式进行土层判定，然后针对不同的土类别，用不同的颜色进行显示，最后综合绘制在一张图谱上，供勘察人员进行综合分析使用。整个算法的流程如图5所示。

按照该流程编写全区域双桥静探综合分析辅助算法，在读取各个孔号名称及相应的地面标高之后，即可自动获取全区域的分层图谱，利用该图谱可以辅助勘察人员对整个勘察区域进行综合分析，确定标准地层表。

1.3.2 实际应用

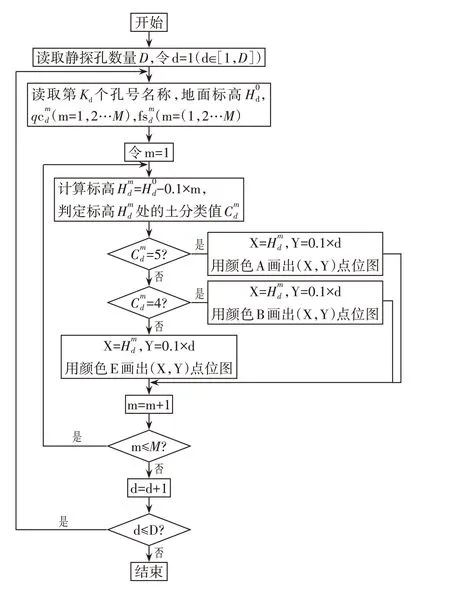
图5 全区域双桥静探综合分析辅助算法流程Fig.5 Flow Chart of Comprehensive Analysis Algorithm For Double Bridge CPT in the Whole Region

在山东某地区进行岩土工程详细勘察，按照采取土试样和进行原位测试的勘探孔数量不应少于勘探孔总数的二分之一，钻探取土试样钻孔的数量不应小于勘探孔总数的三分之一的原则［10］，结合勘察区域实际的地形地貌布置测点，其中共有双桥静力触探试验孔110个，勘察区域地形起伏变化较大，结合现场实际踏勘和钻孔信息，确定表层的填土深度大约为1 m，利用全区域双桥静探综合分析辅助算法，设定0.0～1.0 m深度范围为填土，然后剔除所有静力触探孔在该深度范围内的数据，对所有静探数据进行土层类别判定之后，按照实际标高和孔位排列序号绘制全区域双桥静探综合分析对比图，针对不同的土类别，用不同颜色表示出来，最终结果如图6 所示。为了更明显体现地层变化，图6中将粉质黏土、黏土和软土都统一划分到粘性土中。

图6 全区域双桥静探综合分析对比Fig.6 Comprehensive Analysis Chart of Double Bridge CPT in the Whole Area

图6 展示了勘察区域内部所有110 个静探孔的土层变化情况。从图6中可以看出，在该勘察区域内，地形起伏变化较大，最高处与最低处的高差高达4 m，地下土层的变化也极为复杂，如果只根据现场经验和部分静探孔的土层变化数据，难以有效且准确地认识全区域的地层变化情况，但是通过算法得到全区域双桥静探综合分析对比图之后，就可以在一个维度内同时观察所有孔位的地层变化情况，这就为勘察人员掌握全区域的地层变化提供了有效参考。

以图6为例，根据该图反映的实际土层变化情况，结合单个静探试验孔数据和部分钻孔信息，可以基本确定该区域内部地层变化趋势，现简要概述如下：

①层填土：根据现场踏勘结果和钻孔信息，该层土主要分布在地表以下0.0～1.5 m 范围内，以粉土和粉砂为主要成分；②层砂土：分布区域较小，基本在标高73～74 m 的区域，且层底埋深基本不超过4 m；③层粉土：只在个别静探孔位中出现，且厚度较小，层底埋深基本不超过4 m；④层黏性土：分布区域较小，土层厚度变化较大，层底埋深基本不超过5 m；⑤层粉土：分布较普遍，且土层厚度变化较大，部分孔在该层还夹有少量粉砂或者粘性土；⑥层砂土：分布极普遍，且土层厚度变化较大，在出现该层的大多数孔内部，该层层厚基本都达到4 m 左右。⑦层黏性土：分布较普遍，且土层厚度变化较大，层底埋深基本在9～14 m 范围内；⑧层粉土：分布较普遍，且土层厚度变化较大，层底埋深基本在11～17 m 范围内；⑨层砂土：分布较普遍，且土层厚度变化较大，层底埋深较深，部分孔位未完全揭露。

以上对全区域层位的简单划分主要是基于静探数据的判定得到的，并不能完全反映实际的地层变化，还需要结合土工试验、钻孔信息数据、标贯试验数据、静力触探试验端阻qc和侧阻fs等进行进一步的综合判定，但是通过绘制全区域双桥静探综合分析对比图，可以有效地给勘察人员提供参考，尤其是对粉砂粉土交互沉积地层的划分提供了极大的方便，为标准地层的确定打下坚实的基础。

2 结论及建议

本文介绍了3种针对单桥静力触探试验和双桥静力触探试验的分析算法，通过论述算法原理及流程，同时结合实践数据分析了算法的运行方式，证明了3种算法在利用静探数据分层方面的实用性及便捷性，为勘察人员以后的勘察作业提供了新的思路及手段，可以有效地提高勘察人员的工作效率。

同时应该看到尽管这3种算法能够帮助勘察人员进行层位划分，但都只是一种辅助手段，还需要结合实际经验及其他数据综合分析。此外这些算法还需要进一步接受实践的检验，目前在同时分析多孔静探数据的效率方面仍有不足，需要在后期的工作中进行改进。