支护桩危险点的判定方法研究

何 钦，张记峰，丘北刘

（广东省建设工程质量安全检测总站有限公司 广州510500）

0 引言

支护桩常见于基坑及边坡支护、滑坡治理等工程，用于承载水平方向的土压力或滑坡推力。在支护体系的设计有效期内，一般采用预埋测斜管的方式对支护桩进行水平位移监测。监测单位定期观测并以变形允许值作为支护桩安全稳定性的判定标准，超限报警，向委托方反馈分析建议，为优化设计和指导施工提供依据，保障支护体系和周边环境安全。

在进行支护桩水平位移监测数据分析时，通常认为桩体水平位移最大值处的应力状态是最危险的［1-5］，即危险点。在监测数据超过变形允许值、桩体开裂漏水等异常情况下，采取抢险加固措施时通常基于这个结论展开。但结论并不能涵盖所有情况，如2012 年12 月30 日发生的武汉市轨道交通3 号线王家湾站基坑垮塌事故［6］，项目设计开挖深度20.6 m，采用φ1 000@1 200 灌注桩围护结构，桩长为31.6 m。开挖至17 m 左右时，支护桩在桩顶以下10 m 处折断，引发冠梁破坏和基坑局部坍塌。而断桩处水平位移监测值并非最大值。

因此，支护桩危险点的判断方法应进一步完善，以便更准确地找到支护桩危险点。为此，本文以某项目中的支护桩水平位移监测数据为例，利用有限元分析方法对桩体的应力状态进行了模拟，对桩体最大位移值并非最危险点的情况进行了分析。根据分析结果，本文提出了一种以桩段相对位移判断最危险点的方法，并对该方法的适用性进行了分析和讨论。结果表明，在桩身不存在明显激凸点时，基于桩段相对位移的判别方法能有效找出桩体的最危险点。

1 基于测斜数据的桩体危险点数值分析

为弥补实际工程中桩体水平位移最大值处并非最危险点处而导致的判断不准问题，本文首先利用测斜数据对桩体进行了有限元模拟分析，以找出桩体的最大应力点（危险点）。

1.1 方法介绍

本文建模所用测斜数据近似抛物线型桩，如图1所示，测斜数据间距为0.5 m。由于实际工作中，测斜并非将桩体各处的水平位移均测出，而是按照固定间距测到某一深度为止［7］。因此在构建有限元模型时，其边界条件应选为桩体底部仅限制纵向位移（重力方向）的单向约束，如图1b 所示。该约束条件可考虑最后一个测点（最深处）水平位移对该点以上桩体的影响。同时，不限定该点转动，即认为该点仍可因弯矩而产生转角，使其与实际情况相符。

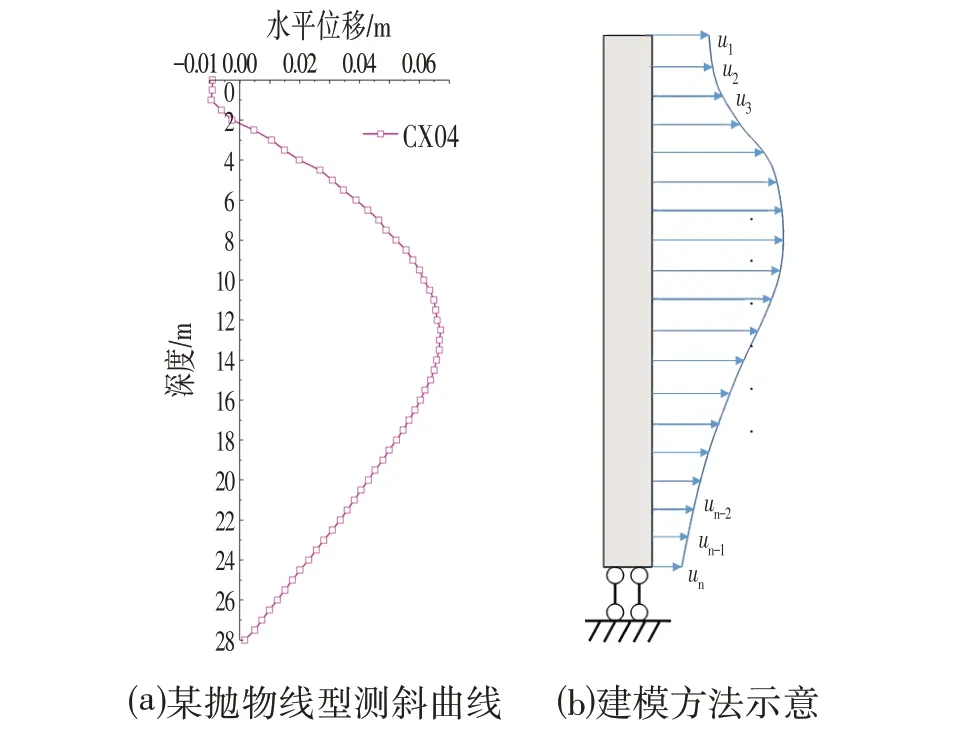
图1 某抛物线型测斜及建模方法示意Fig.1 Schematic Diagram of a Parabolic Inclinometer and Modeling Method

模型边界设置后，参考位移法［8］，将各深度的水平位移作为边界约束条件作用在桩身各处，即以若干个集中荷载去逼近实际的外荷载条件，并限定其各点位移与实际相同。以此方法可以逼近桩体真实的受力情况，已知水平位移测点数越多则计算结果越接近实际。参考工程实例将支护桩截面取为直径为1.2 m的圆形截面，单元类型为B22 梁单元，单元尺寸统一取为1 cm；其中，钢筋混凝土的弹性模量E=31.5 GPa，泊松比ν=0.2。为使计算结果区分度更为明显，本文选用的抛物线数据为一事故基坑的监测数据，此时桩体位移值已超过允许位移值。

1.2 模拟结果分析

模型计算得到全桩的主应力面最大主应力和最小主应力的分布曲线如图2所示。

图2 应力分布曲线Fig.2 Stress Distribution Curve

由于建模时桩单元局部坐标选择以向上为正。因此，最大主应力对应着最大拉应力，而最小主应力对应着最大压应力。经对比，桩体最大拉应力出现在4.53 m 深度处；最大压应力处为1.06 m 深度附近。由于桩体最大水平位移位置分别为深度1.0 m（最大负水平位移）和12.5 m（最大正水平位移）处。因此，可以得出结论，桩体水平位移最大处并不一定是桩体应力状态最危险处。上述结果说明，除采用规范规定的最大位移点对桩体危险点进行判别外，还需采用有限元分析等其他方法对其进行辅助判别。

2 判断桩体危险点的桩段相对位移方法

在1.2 节分析中，本文通过数值分析再次说明了桩体最大水平位移值处不一定是最危险点的问题；说明实际工程中为确保桩体的及时二次支护，需要补充其他方法对桩体最不利应力位置进行分析。而利用桩体所有测斜数据对工程中所有桩体进行有限元建模分析，存在实际操作上的困难。为此，本文进一步提出了以桩段最大相对位移（相对位移法）对桩体最危险点进行判断的方法，并对该方法的适用性利用有限元模拟分析进行了讨论。

2.1 相对位移判别法

根据等距间隔的监测数据将桩体分割成多段小短桩，可以单独研究其小段内的挠度变化。参考《建筑变形测量规范：JGJ 8-2016》［9］给出的挠度计算公式⑴（见图3），将各小段两端的水平位移监测数据视作梁段的整体位移进行扣除，则可以根据小段中点的水平位移计算出小梁段中点的相对挠度f1。

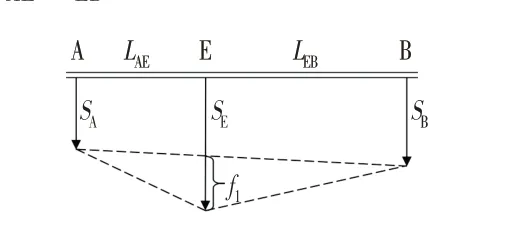
图3 挠度计算方法Fig.3 Deflection Calculation Method

以图1中抛物线型测斜曲线为例，经计算，该抛物线型变形桩体的各点换算的挠度（相对位移）按桩身方向绘制曲线如图4所示。

图4表明，桩体的最大正相对水平位移位于4～5 m深度间，而最大负相对水平位移则位于1 m深度附近；这一结果与1.1 节中有限元分析得到的最危险位置相符。说明相对位移法具有实用的可能性。

2.2 相对位移法适用性分析

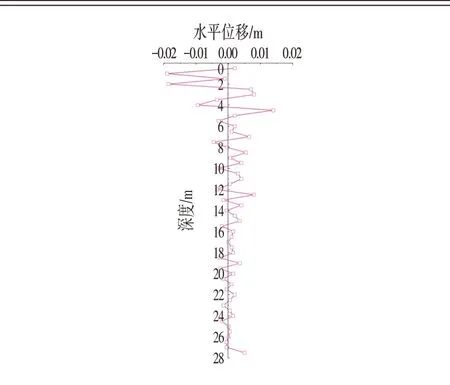
图4 抛物线型测斜数据换算后桩相对位移曲线Fig.4 Pile Relative Displacement Curve after Conversion of Parabolic Inclinometer Data

2.1 节的换算结果说明相对位移法与利用所有测斜数据的有限元分析方法得到的危险点结果较为一致，但其对危险点的预测是否合理还需进一步的分析讨论。为此，本文按照监测数据将桩体截成多段两端固定梁体，将最大相对位移段取出单独进行有限元模拟计算，并将其最大应力与全桩的有限元计算结果进行对比。然而，在实际案例中［10，11］，除连续光滑的抛物线型类测斜曲线外，还存在桩体变形出现突变点的激凸型测斜曲线（见图5）。相对位移法对具有不同变形特征的桩体危险点的预测适用性可能存在明显区别。为此，本文同时选用了2 组分布特点相差较大的连续光滑型（抛物线型）和曲线有较大凸变值的激凸型测斜曲线进行分析，以研究相对位移值作为桩体危险点分析方法的整体可行性。

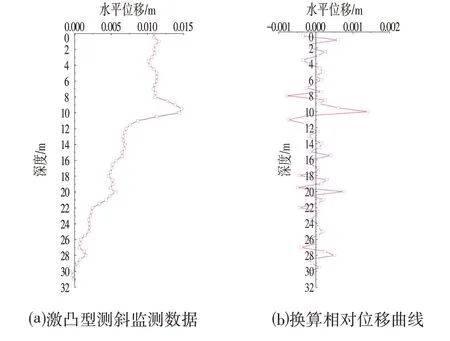
图5 激凸型测斜监测数据和换算相对位移曲线Fig.5 Monitoring Data of Protruding Type Inclinometer and Conversion Relative Displacement Curve

2.2.1 建模方法

其具体建模思路如下：由于小梁段两端的水平位移作为小梁段的整体位移扣除，因此小梁段应不存在水平和竖向位移，而仅存在由于弯曲而产生的转动。因此建立模型时应约束小梁段的水平和竖向位移，而不约束转动，如图6a 所示。加载时，模型选为位移加载，在梁端中间施加计算得到的相对位移值。小梁段的梁单元局部坐标亦选择向上为正反向，局部坐标选取如图6b所示；梁单元截面尺寸和材料参数均设置与全桩计算相同。

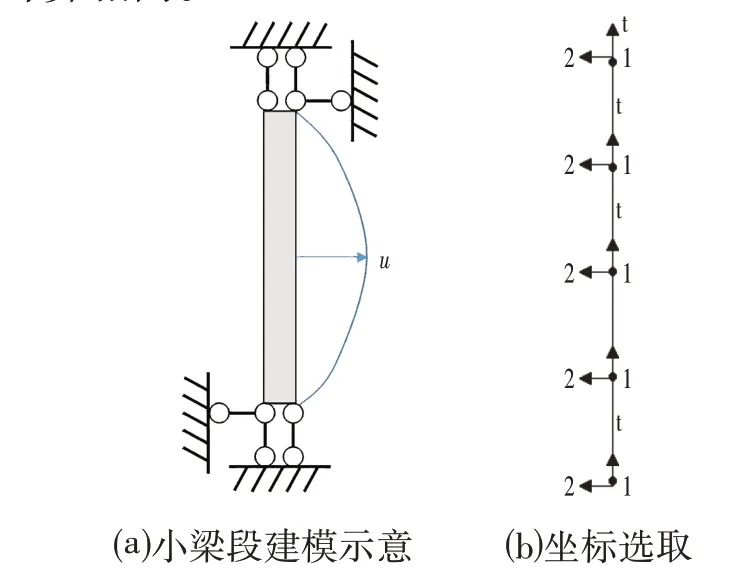
图6 小梁段建模示意及其坐标选取Fig.6 Modeling of Trabecular Segment and its Coordinate Selection

模型计算所用加载位移值分别采用抛物线型（见图4）以及激凸型测斜数据（见图5）的最大和最小（负值）相对位移值。其中，图5b 中的相对位移曲线是利用图5a 中数据根据式⑴换算所得。因图中有较明显的位移突变点而命名为激凸型测斜曲线（见图5a）。该激凸数据来自一处于安全状态的基坑。

2.2.2 模拟计算结果与分析

经计算，抛物线型测斜数据换算得到的最危险梁段的最大正相对水平位移和最小水平位移计算结果分别如图7所示。

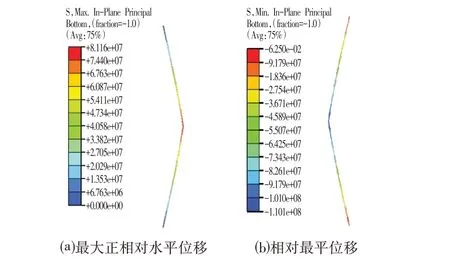
图7 抛物线型变形桩桩身最大正相对水平位移和最小水平位移计算结果Fig.7 The Maximum Positive Relative Horizontal Displacement of the Parabolic Deformed Pile Minimum Horizontal Displacement Calculation Result

图7 表明，最大正相对位移段的最大拉应力为8.116×107Pa，而全桩计算的对应结果为8.163×107Pa；最大负相对位移段最大压应力为1.101×108Pa，而全桩计算结果相近位置处应力大致为1.492×108Pa。说明小梁段简化单元的计算结果十分接近桩体整体计算的结果。相对位移法替代有限元分析方法用于辅助判别抛物线型变形桩体的适用性较好。

与之相应，激凸型曲线的桩体有限元建模计算结果如图8、图9所示。

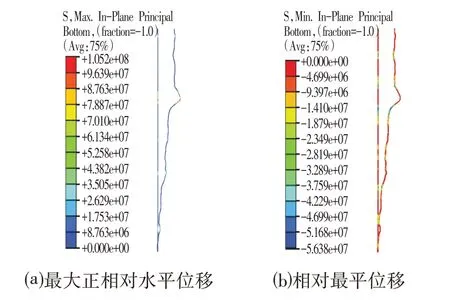
图8 激凸型桩体全段应力分布情况Fig.8 Stress Distribution of the Whole Section of the Excited Convex Pile

图9 激凸型桩体小梁段应力分布情况Fig.9 Stress Distribution of Small Beam Section of Stimulated Convex Pile

根据图8可知，全桩段分析时，激凸型变形桩体最大拉应力和最大压应力位置分别位于深度9.902 43 m和10.051 90 m 处。而根据图9 相对位移曲线找到的正负最大位移点分别为10.0 m 和8.0 m。说明存在激凸时，对应最大正相对位移点与整体计算结果的拉应力最大点较接近，但其最大负相对位移点仅对应整体计算结果的压应力较危险点，而不是压应力最危险点。因此，当曲线存在明显的激凸点（曲线欠光滑，二阶导数不为0）时，用相对位移判断的方法可能会错过最危险点。此外，从计算结果可以看出，处于安全状态的激凸测斜曲线算出来的最大应力值已接近危险基坑（抛物线形）的计算结果，说明激凸形变形的桩体较平滑变形的桩体更为危险。

造成桩体激凸变形的可能原因有很多，一般是因为桩体本身或外荷载导致桩体受力情况不能保持平滑的过渡，例如桩身存在缺陷，桩后土体不均匀等情况。因此，利用短梁段相对位移分析的方法可能因为简化条件不满足而产生过大误差；又或者因激凸变化的最大点没有被监测点覆盖而不能反应其最危险位置。不过，根据激凸型变形桩体全段有限元计算结果不难发现，激凸点一般为最危险受拉点；而激凸峰的突起两端点一般为最危险受压点。这一结论可以有效辅助判断桩体的最不利受力位置。

3 结论

由于文献［7］以桩体测斜水平位移绝对值作为判断桩体危险点的主要判据，而实际工程事故表明存在例外，即桩体破坏点并非位移最大点的情况。为优化判断方法，本文以某工程实测桩体测斜数据为例，通过有限元数值分析方法对其进行了探索和讨论。本文先根据测斜数据作为位移量进行梁单元受弯情况分析，对桩体水平位移最大点并非应力最大点的问题进行了讨论；之后给出了一种利用相对位移进行危险点判断的方法，并利用截取小梁段进行有限元分析计算的方式对其适用性进行了讨论。根据建模分析结果，本文得出如下主要结论：

⑴本文提出了一种较为简便的桩体危险点判别方法——相对位移法，在桩体变形为连续光滑曲线时，该方法可得到与有限元位移分析较为接近的计算结果，以辅助判断桩体的最不利受力位置。

⑵当桩体变形曲线出现明显激凸点时，采用相对位移法不一定能准确地找出桩体最不利位置，存在错过最危险点的可能性。

⑶激凸型变形桩体的激凸点一般为最危险受拉点；而激凸峰的突起两端点一般为最危险受压点。这一结论可以有效辅助判断桩体的最不利受力位置。

本文所得结论均基于连续体有限元分析，将桩体视为均质弹性体，这在桩体出现较大塑性变形时可能并不适用。但本文给出的相关规律和判断方法可为工程实践提供参考。至于桩体的塑性变形状态分析有待进一步的试验和理论研究。