考虑机器故障的作业车间调度方案鲁棒测度方法
巴智勇,袁逸萍+,戴 毅,李晓娟,阿地兰木·斯塔洪,刘金朵
(1.新疆大学 机械工程学院,新疆 乌鲁木齐 830047;2.新疆生产力促进中心,新疆 乌鲁木齐 830099)
0 引言
作业车间作为产品制造的直接执行者,承载着大量的生产任务,生产任务间存在着复杂的关联关系。随着生产系统规模的扩大和复杂性的提高,生产系统运行中的不确定因素急剧增加,对于生产系统的影响难以估计,如果车间管理者无法提前或及时进行资源调度和计划调整,极易导致生产进度的拖延和生产成本的上升,严重时引起生产过程混乱。
在实际生产过程中,机器故障是常见的不确定因素,它不仅会导致实际生产结果和计划产生偏差,还可能引起物料配送等相关生产环节的混乱,对生产过程带来重大影响。因此,在制定调度方案时考虑未来机器故障干扰,可以有效减少机器故障对调度性能的影响。如何有效评估故障环境下调度方案的性能成为鲁棒性调度的一个难点。
近几十年,大量学者对于生产过程中存在机器故障的鲁棒调度问题进行了深入的研究。由于在生产之前无法得到实际生产数据,蒙特卡洛仿真(Monte Carlo simulation, MC)和替代测度(Surrogate Measure, SM)是常用的两种鲁棒性测度方法。
(1)基于蒙特卡罗仿真的测度方法
Zandieh等[1]通过免疫算法求解随机机器故障下混合流水车间调度问题,通过故障模拟器评估可行调度方案的期望完工时间,将其作为选择适应度值对种群进行选择,引导算法生成期望时间较小的调度方案。张先超等[2]针对设备故障下多阶段流水车间的调度问题,将生成的调度方案在故障环境下运行100次,将平均工期和工期标准差作为调度方案的性能和风险测度。Shen等[3]使用场景表示扰动的随机性,进而提出两种替代性测度方法,并通过仿真实验证明其有效性。Amirl等[4]通过仿真软件建立大量扰动场景,评估可行调度方案的性能,并通过对仿真数据进行训练,构建调度决策神经网络。Al-Hinai等[5]研究了随机机器故障下柔性作业车间的鲁棒调度问题,以工序完工期偏差为基础提出3个鲁棒性指标,通过模拟大量的故障场景来评估调度的鲁棒性。顾泽平等[6]针对多种不确定因素环境下柔性作业车间的多目标调度优化问题,提出使用离散仿真方法来评估调度方案的性能,引导混合遗传算法的进化方向,并通过对比试验证明了所得近似最优解具有更高的鲁棒性。
(2)替代测度方法
针对单机鲁棒调度问题,Mehta等[7]详细给出了5种替代测度,并进行了比较,提出了基于替代测度的鲁棒调度算法。Goren等[8]根据机器加工时间和机器维修时间提出了两种替代测度,并通过仿真验证了替代测度对单机鲁棒调度的有效性。陆志强等[9]针对考虑预防性维护的流水线鲁棒调度问题,提出一种替代测度,并基于替代测度设计三阶段启发式算法对模型进行求解。Leon等[10]研究了作业车间鲁棒性调度问题,以所有工序的平均总松弛(total slack)时间为替代测度,将该替代测度嵌入到遗传算法中,引导算法生成鲁棒性调度方案。Xiao等[11]结合调度方案和工序加工时间的分布信息,考虑关键路径和非关键路径对调度鲁棒性劣化的影响,提出了两种替代性的鲁棒测度,并通过仿真实验证明其有效性。Al-Fawzan等[12]用自由松弛(free slack)时间之和来测度资源受限项目调度的鲁棒性。Xiong等[13]考虑机器负载与故障的相关性,用机器负载来表示工序总松弛时间的重要性,提出工序加权总松弛时间之和来近似调度方案的鲁棒性。Wu等[14]结合工序松弛时间和故障信息提出一种调度鲁棒替代测度方法,评估调度完工期的延迟风险。
以上成果都为本文的研究工作提供了借鉴和参考。蒙特卡洛仿真虽能有效评估调度鲁棒性,但求解速度慢;同时多数替代性测度方法,由于未能充分利用故障信息,导致评估的准确性下降,若要有效利用故障信息需要解决以下两个难点:①机器故障的随机性和造成的影响在传播过程中的不确定性;②多个机器故障在传播过程中的叠加效应。
因此,本文结合调度方案结构、机器故障概率和维修时间提出一种基于期望影响效应的替代性测度方法,首先由机器故障分布函数计算工序加工过程中机器发生故障的概率,简称工序故障概率,同时得到工序加工过程中机器平均维修时间,简称工序期望维修时间,将机器故障映射到工序层面,分析单工序故障影响的传播效应,进而评估多工序故障影响的综合效应,获得各工序的期望完工时间,最终求解出调度鲁棒性。
1 机器故障下作业车间鲁棒性调度问题描述与假设
为表述方便,表1列出了文中用到的符号及其说明。

表1 符号表示及其说明

续表1
1.1 机器故障下车间作业调度问题描述与假设
作业车间调度问题可描述为:n个工件在m台机器上加工,每个工件有特定的加工工艺,使用机器的次序一定,加工时间为常数;工件在0时刻到达,所有机器在开工前均可用,每台机器同一时间只能加工一个工件。在生产前调度计划已经制定,且在加工过程中工序在机器上的加工顺序不变。
本文的研究对象是可行的调度方案,各工件在机器上的加工时间和加工次序已确定。当发生故障时存在以下假设:
(1)机器故障只发生在机器加工期间;
(2)加工过程仅当机器发生故障时允许中断,在维修后继续加工,受到影响工序采用右移策略进行控制;
(3)维修操作不改变机器役龄。
1.2 随机机器故障描述
随机机器故障可以用故障发生概率与维修时间两个参数进行描述,一般认为机器故障是服从一定的概率分布,机器的维修时间为定值。本文假设机器的可靠性服从Weibull分布。
机器在t时刻的可靠性为:
(1)
式中:λ(t)为故障率函数;β为形状参数,当β>1时,随着t的增加,机器故障概率逐渐增大;θ为尺寸参数。
1.3 调度方案鲁棒性测度指标
调度的鲁棒性指调度在不确定环境下保持原有状态或性能的能力,通常分为性能鲁棒性(Performance Robustness, PR)和调度稳定鲁棒性(Stability Robustness, SR)[15]。性能鲁棒性是指初始调度的目标值与不确定因素扰动下实际调度目标值的接近程度。调度稳定鲁棒性指扰动因素影响下实际执行的调度与初始调度的接近程度。
(1)性能鲁棒性
用实际调度的σr与原调度σp期望最大完工时间偏差作为原调度σp的性能鲁棒性测度,可表示为:
PR(σp)=E[|Cmax(σr)-Cmax(σp)|]。
(2)
由于原调度σp受到机器故障的影响,工序的完工时间不会减小,即Cmax(σr)-Cmax(σp)>0修改为:
PR(σp)=E[Cmax(σr)]-Cmax(σp)。
(3)
式中:原调度方案的Cmax(σp)已知,而E[Cmax(σr)]为实际调度σr中工序最大的期望完工时间。
(2)稳定鲁棒性
用实际调度σr与原调度σp各工序期望完工时间偏差之和表示稳定鲁棒性,可表示为:
(4)
同理,式(4)修改为:
(5)
式中,原调度方案中各工序的完工时间已知,E[Ci,j(σr)]表示实际调度σr中各工序的期望完工时间。
由以上分析可知,两类调度鲁棒性指标都转化为工序期望完工时间的求解问题。但在生产完成之前,无法得到实际调度各工序完工时间,难以评价原调度方案的鲁棒性。
2 基于故障影响传播效应的鲁棒性测度
2.1 作业车间工序关联关系分析
工序在制造资源加工时序上存在次序性,在工艺上存在顺序性,使得工序间存在复杂关联关系。为描述工序间关联关系,给出以下定义。
定义1关联工序。由于机器共用和工艺的顺序性,使得工序间存在时间约束关联:先加工工序时间的减少或增加可能引起后加工工序时间的提前或延迟。
先加工的工序称为前向关联工序,后加工称为后向关联工序,若关联工序加工的先后顺序是紧邻的,同一工件紧后加工的工序,记作工件维紧后工序,同一机器紧后加工的工序,记作机器维紧后工序。
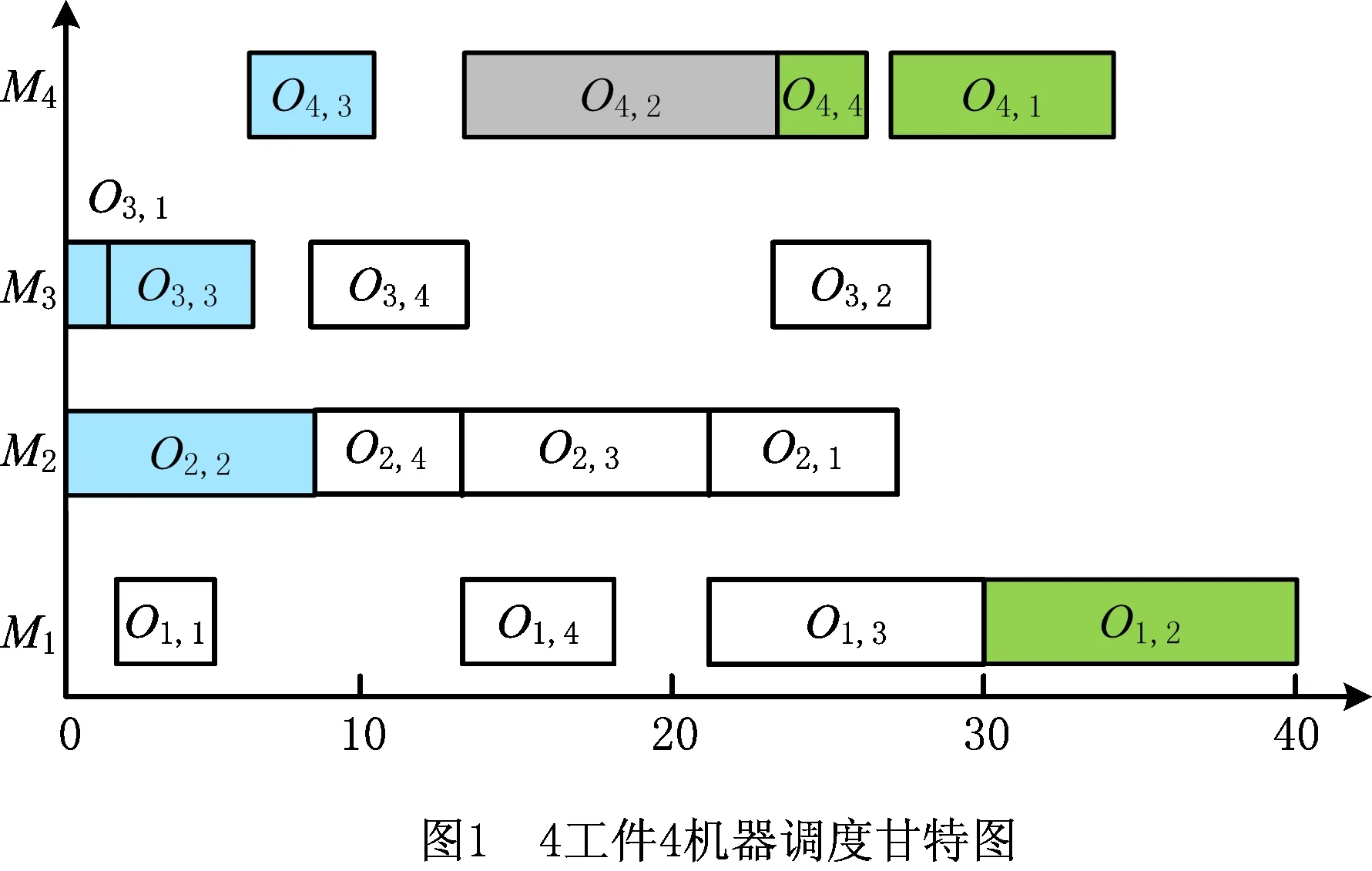
以图1中工序O4,2关联工序分析为例,按工序加工次序可将O4,2关联工序分为前向关联工序集合{O3,1,O3,3,O4,3,O2,2}和后向关联工序集合{O4,4,O4,1,O1,2}。前向关联工序集合中任意工序的加工时间变化可能会导致O4,2的延迟,如前向关联工序O3,1与O4,2既不是同一工件的工序也不在同一机器加工,但工序O3,1的加工时间变化会通过工序O3,3、O4,3间接影响工序O4,2的完工时间。
定义2影响传播链。关联工序及其之间工序组成的有序集合,集合中的工序至多存在一个紧前关联工序和一个紧后关联工序。如图1中O3,1与O4,2之间的影响传播链为{O3,1,O3,3,O4,3,O2,2}。

2.2 工序关联下故障影响效应分析
机器故障导致工件的加工过程发生中断,由于本文假设工件在机器修复后继续加工,机器故障实质上增加了工件在机器上的停留时间[2],在工序层面,可视作工序加工时间的增加。本文通过机器故障概率分布函数,将机器故障映射到工序层面,得到各工序的故障概率,如式(6)所示:
pri,j=1-e-[(ai,j/θ)β-(bi,j/θ)β]。
(6)
式中:ai,j为工序Oi,j开工时机器Mi的役龄;bi,j为工序Oi,j加工完成时机器Mi的役龄。
式(7)给出了工序Oi,j的期望维修时间:
(7)



2.3 鲁棒性测度
作业车间调度问题中,各工序具有约束松弛度紧、约束内联度高等特点[17]。当多个工序发生故障时,各工序故障将沿着约束链进行传播并在该过程中出现叠加影响的效应。

如图3所示,工序O1,1的前端关联工序集合为{O2,1,O2,3,O1,2};按工序间存在的时序约束,前向关联工序可分为Path1和Path2两条传播路径。
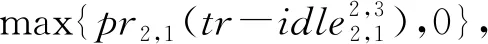
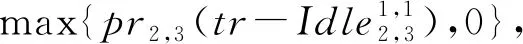

工序O1,1的完工时间期望延迟是两条传播路径上工序造成延迟累计最大值为DT1,1=max(DT(1)1,1,DT(2)1,1)}。

根据以上分析,定义工序由前向关联工序造成延迟时间
DTi,j=max(DT(1)i,j,…,DT(k)i,j)。
(8)
式中DT(k)i,j为第k个影响路径上工序对Oi,j造成的累计期望延迟。

根据调度性能鲁棒性的定义,将工序的期望完工时间带入式(3),可得到调度的性能鲁棒性为:
cmax(σp)。
(9)
同理可得调度稳定鲁棒性为:
(10)
3 算法设计
根据上述分析,本文设计一种基于故障影响效应的调度鲁棒测度求解算法,符号说明如表2所示,具体算法如下:
输入原调度σp(工件在机器上的加工顺序,各工序加工时间、开工时间、完工时间),Weibull分布函数的形状参数β,尺寸参数θ,故障维修时间tr。
步骤1确定未添加期望维修时间工序集合NDO和已添加的工序集FDO,并对以下集合、变量初始化FDO←∅;NDO←TO;PAO←∅;AO←∅;STAO←∅;ETAO←∅;k=0;a=0。
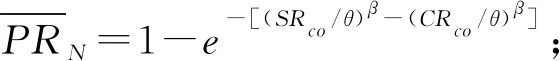
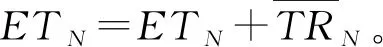
步骤4若CO∉AO,则AO←AO∪{CO},STAO←STAO∪{STN},ETAO←ETAO∪{ETN},a←a+1,否则,确定出当前工序CO在AO中编号a′,更新AO[a′]=CO;更新STAO[a′]=max{STN,STAO[a′]},ETAO[a′]=max{ETN,ETAO[a′]}。
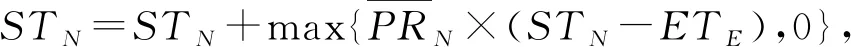
步骤6从工序集ARO中删除CO,转步骤5。
步骤7遍历受影响工序完工集合ETAO,计算受影响工序完工时间ETAO(Oij)与原调度方案工序完工时间Ci,j(δp)的差值并求和,获得稳定鲁棒性指标;计算受影响工序完工时间ETAO(Oij)的最大值max(ETAO(Oi,j))与原调度方案Cmax(σp)的差值,获得性能鲁棒性。

表2 算法中用到的符号及说明
4 仿真验证
4.1 仿真方案设计
为验证本文测度方法的有效性,从典型的基准案例库中选取25个作为实验案例;Adams[18]设计的2个案例(abz5,abz9)、Fisher和Thompson[19]设计的2个案例(ft10、ft20)、Lawrence[20]设计的8个案例(la01、la06、la11、la16、la21、la26、la31、la35、la40)、Storer[21]设计的4个案例(swv01、swv06、swv11、swv16)、Vaccari[22]设计的8个案例(tai01、tai11、tai21、tai31、tai41、tai51、tai61、tai71)和Yamada[23]设计的案例yn1。
采用Windows 2008 Server,3.0 GHz CPU,4 G内存,Python3.5作为仿真语言。
使用Della Croce等[18]提出的遗传算法生成25个案例的不考虑机器故障的调度方案,以最小化makespan为调度目标。设置种群规模为300,交叉率为0.7,变异概率为0.05,迭代次数300。终止条件满足迭代次数。本文假设机器可靠性服从Weibull分布,其中形状参数β=2,尺寸参数θ分为3类,分别为调度方案中机器最大负载的0.5倍、1倍和1.5倍;4类机器故障维修时间tr分别为10,20,30,60;共存在300个实例。求解各案例在随机机器故障环境下调度方案σp的性能鲁棒性PR(σp)、稳定鲁棒性SR(σp)和期望完工周期E[Cmax(δp)]。本文采用蒙特卡洛实验模拟随机机器故障场景,每个案例执行5 000次,获得期望完工期完工期偏差期望值(PRMC)和工序时间偏差期望总和(SRMC)和E[Cmax(σr)]作为真实值。
4.2 有效性分析
为检验测度方法的有效性,设计2个指标来检验测度方法得到结果的精度。PRD(PR(σp),PRDMC)表示PR(σp)与PRMC相对偏差,SRD(SR(σp),SRMC)表示SR(σp)与SRMC的相对偏差,相对偏差越小,说明所提方法的测度结果越精确。
(11)
(12)
表3是25个案例在θ,tr组合成的12种故障水平下的仿真结果,由于每种故障水平下存在25个案例,表3中数据均为25个案例在各故障水平下相应指标的平均值。由表3可以看出,PRD(PR(σp),PRMC)的值均小于0.21%,说明提出的方法对调度性能鲁棒性的测度精度平均可达到99.79%以上,同样的SRD(SR(σp),SRMC)的最大值仅为5.81%,说明提出的方法对调度稳定鲁棒性的测度精度平均可达到94.19%以上,可以有效地表征调度的稳定鲁棒性。由于本方法可以同时求得PR(σp)和SR(σp),两者求解时间相同,用T1表示;η在[0.58%~0.87%]之间,说明本文提出方法的运行时间远远小于蒙特卡罗仿真方法,证明了本文算法的高效性。

表3 有效性分析
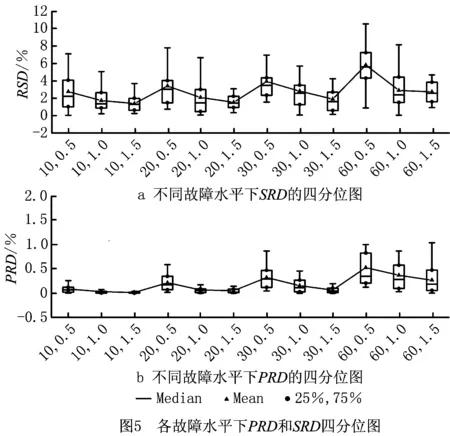
图5为不同故障水平下PRD(PR(σp),PRMC)和SRD(SR(σp),SRMC)分布的四分位图。由图5a可知,当维修时间tr相同时,随着θ的增加,SRD(SR(σp),SRMC)略有下降,由式(6)可知,θ越大时,机器故障概率越低,说明测度方法在低机器故障率环境下的测度精度更高且波动范围较小。当θ相同时,随着维修时间tr的增大,SRD(SR(σp),SRMC)略有上升,说明维修时间的增加对稳定鲁棒性测度的精度有所下降。图5b可得,PRD(PR(δp),PRMC)在各故障水平下保持极小的误差,随着维修时间tr增大,PRD(PR(δp),PRMC)的波动略有增大,但都保持在1%以内,说明本文方法对调度性能鲁棒性的测度精度极高。
4.3 相关性分析
Leon等[10]认为当调度方案中存在更多总松弛时间时,可以更好地减少调度方案的延迟风险,从而提出了基于工序平均总松弛时间的鲁棒性测度方法,如式(13)所示:
(13)
式中ti,j为工序间总松弛时间。
Al-Fawzan等[12]提出使用工序自由松弛时间总和的鲁棒性测度方法,如式(14)所示:
(14)
式中tfi,j为工序间的自由松弛时间。
Xiong等[13]认为负载越大的机器发生故障的概率越大,该机器上的工序总松弛时间越重要,因此提出了工序总松弛时间加权和作为鲁棒性的测度方法,如式(15)所示:
(15)
式中wi,j为Oi,j所在机器的负载,wtot为所有机器负载之和。
为了进一步说明提出测度方法的有效性,对3种替代方法和本文所提方法与实际调度鲁棒性进行线性相关分析(如表4),分析发现,判定系数R2越接近1,线性拟合效果越好。由于实际调度鲁棒性不能提前获得,使用蒙特卡洛仿真得到的PRMC和SRMC作为实际调度的性能鲁棒性和稳定鲁棒性。

表4 相关性分析
从表4可知,SR(σp)的判定系数R2远大于其他3种替代性方法,说明SR(σp)与实际调度稳定鲁棒性的线性相关性很强,同样可得PR(σp)的判定系数R2均优于其他三种替代性方法,且R2均大于99%,说明PR(σp)与实际调度性能鲁棒性线性相关性极强。
图6a表示不同的测度方法与SRMC的判定系数R2在不同故障水平下的变化情况,从图6a中可以看出SR(σp)与SRMC判定系数R2都保持在90%以上,且随着参数变化的幅度较小,保持较高的稳定性。而另外3个替代性指标RM1、RM2、RM3与SRMC的相关性均在30%以下,表明三者与SRMC的相关性很差,不能替代表示调度方案的稳定鲁棒性。
图6b表示对于不同测度方法与PRMC判定系数R2在不同故障水平下的变化情况,从图6b中可得PR(σp)不随着维修时间和机器故障概率变化,保持较高的稳定性,同时R2均保持在99%以上,说明PR(σp)与PRMC几乎是线性相关。而RM1和RM3与PRMC的判定系数R2保持在30%~60%之间,存在一定的线性相关,随着参数变化存在一定的波动性。RM2与PRMC的判定系数R2在70%~90%之间,说明RM2与PRMC相关性较高,但随着tr的增加相关性有所下降。

5 结束语
本文研究了设备故障环境下作业车间的调度鲁棒性的测度问题,从工序关联角度分析机器故障及其扩散效应对调度鲁棒性的影响,提出了基于故障传播效应的测度方法并设计求解算法,仿真结果显示本文提出的测度方法对于调度性能鲁棒性的测度精度可达到99.79%以上,对调度稳定鲁棒性的测度精度可达到94.19%以上,证明本文方法的测度有效性。通过相关性分析,得到本文方法在各种故障水平下与蒙特卡洛方法的结果均能保持较高的相关性,并与其他3种替代性测度方法比较,证明了本方法的优越性。
本文提出的方法可为故障环境下鲁棒性调度提供精确的测度方法,引导算法生成。在动态调度问题中,可通过评估机器故障对调度性能影响程度,准确选择调度时机和重调度策略。未来将进一步研究集成预维护活动的调度方案的风险评估及预维护活动的插入策略,并对机器故障环境下作业车间重调度时机和策略进行研究。

