基于PH 分布的多服务器小型有线通信网络稳态性能研究

王 清 ，吴 倩 ，刘以群

(1.91033 部队，山东 青岛266000；2.海军工程大学海军舰船振动与噪声研究所，武汉430033；3.船舶振动噪声重点实验室，武汉 430033；4.中南财经政法大学继续教育学院，武汉430064)

0 引言

小型有线通信网络系统的运行过程中，由于服务器数量和资源有限，如果出现通信高峰，会产生排队现象。此时要充分考虑用户终端的耐心，尽可能地减少用户终端的排队等待时间，避免出现长时间排队等待加载的现象。数学排队论模型为小型有线通信网信息交换机制的优化提供了新的方法。

PH 分布族在经历过大量运算后依然具有封闭性，同时能近似拟合非负半轴上的任何概率分布，可将各类典型分布统一表示为Phase-type(PH)形式，降低了解析计算难度，又具有一般性，使得其被广泛应用于各类随机模型。

综上，本文以小型有线通信网络系统为研究对象，引入连续PH 分布描述系统中各随机时间变量，基于排队论建立了通用性更好的小型有线通信网络系统稳态性能解析模型，给出了相关稳态指标。

1 相关基础知识

为进一步说明连续PH 分布在小型有线通信网络系统稳态性能分析中应用的可行性，下面对PH 分布的相关定义和性质进行简要介绍：

定义 1［1］：若一个非负随机变量服从连续 PH 分布，那么它的分布函数为：

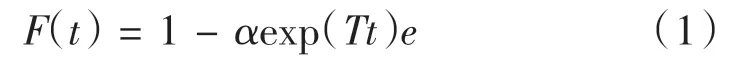
其中：

(1)e 是全部元素都为1 的列向量；

(2)α 是次随机矩阵，含m 个非负元素的行向量，m 为正整数，αe ≤ 1；

(3)T 是m 阶矩阵，该矩阵对角线元素全为负，其他元素非负，矩阵可逆，且每行元素之和是非正的。

定义 2［1］：连续时间马尔科夫链{I(t)，t ≥ 0}，其状态空间由m + 1 个状态组成，无穷小生成元表示为：

其中，T 为PH 分布的生成元。由于每一行元素之和均为0，则可得T0= -Te。状态m + 1 的转移概率为0，则状态m + 1 为吸收态。

定义 3［2］：一个 m × n 阶矩阵 A 和一个 p × q 阶矩阵B 的Kronecker 积被定义为：

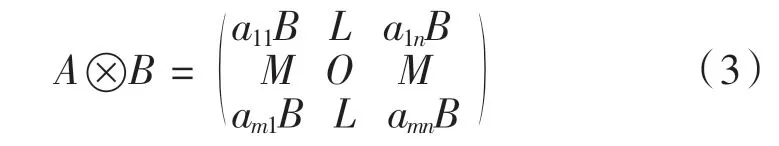
根据式(3)，可得出Kronecker 积有如下性质：

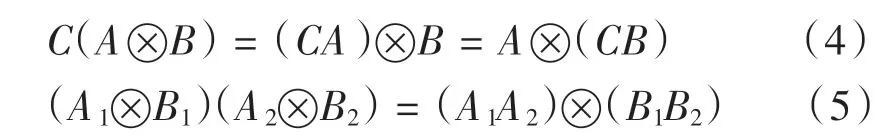
定义 4［2］：一个 m 阶矩阵 A 和一个 n 阶矩阵 B 的Kronecker 和被定义为：

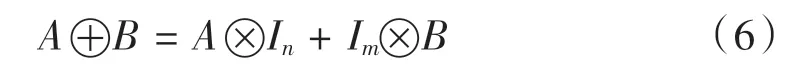
其中，In和Im分别表示m 和n 阶的单位矩阵。

2 问题描述

某有线通信网络系统中由服务器和用户终端组成，是排队论中典型的M/M/C 队列，具体假设如下：

(1)系统中有有限的n 个服务器和m 个用户终端，m ＞ n；

(2)各服务器资源被占用时间服从随机分布，假设服从连续PH 分布，形式为k 阶的(α，T)表示；

(3)两用户终端到达服务器时间间隔服从随机分布，假设服从连续PH 分布，形式为g 阶的(β，S)表示；

(4)当服务器全部占用时，用户终端采用等待制的模式进行先到先服务的排队；

(5)各服务器资源被占用时间、两用户终端到达服务器时间间隔相互独立。

3 模型构建

3.1 用户终端排队规则

对于有线通信网络系统来说，当多个用户终端同时进入服务器中出现排队现象后，要对用户终端进行排队规则的设定以确定服务器资源占用次序。

排队原则是当系统中服务器没有排队现象时排队规则为先到先服务，各服务器优先级相同，具有相同的性能和信息传递水平；当系统中服务器均被占用时，系统会出现排队现象，会有用户终端在等待访问服务器，等待的用户终端在有服务器空出时依然按照先等待先进入的规则访问服务器；当有多个服务器同时空出时，用户终端随机进入某一服务器。

针对于小型有线通信网络系统，一般设置2 ～3个服务器进行信息交互传输，工作时采取串行或并行作业的方式，设置为多窗口混合型排队系统，如图1 所示。

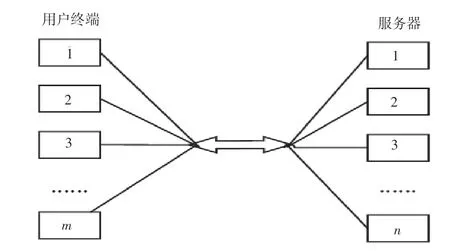
图1 有线通信网络混合型排队系统

3.2 系统状态转移

根据用户终端和服务器的运行规则和排队规则，可得小型有线通信系统状态转移图如图2 所示。

图2 有线通信网络状态转移图

其中，状态(0，n)表示系统中有0 个用户终端传输数据，有n 个服务器空闲，以此类推。直到状态(n，0)为止表示系统中有n 个用户终端传输数据，无空闲服务器。状态(m，m - n，0)表示系统中有有n 个用户终端传输数据，无空闲服务器，m - n 个用户终端排队等待。

结合PH 分布的相关定义，对各状态之间的转移率进行分析，从状态(0，n)到状态(1，n - 1)的状态转移矩阵为 S0α，以此类推，直至从 S0α；而后，从状态(n，0)到状态(n + 1，1，0)的状态转移矩阵为直至状态(m，m - n，0)。

反之，从状态(m，m - n，0)到状态(m - 1，m - n -1，0)的含义是某一用户终端已完成服务器数据交互，等待的用户终端按排队规则进入服务器，其状态转移矩阵为直至状态(n，0)为止；从状态(n，0)到状态(n - 1，1)表示某一用户终端已完成服务器数据交互，这一服务器空闲，其状态转移矩阵为T0β，直至状态(0，n)为止。

根据各状态转移矩阵，可得出该小型有线通信网络系统状态转移矩阵Q 为：

3.3 系统稳态概率向量

有线通信网络系统按照这一排队规则在经历长时间运行之后会进入稳定状态。当系统处于稳态时，其各状态在相互转移的过程中停留在每个状态的概率可以构成稳态概率向量π，可分解为π =(π0，π1，π2，…，πm)，根据稳态概率向量的相关性质［3］可知其满足下列方程组：

利用矩阵解析方法［4］对其进行求解，引入转移率阵 R*，令 R*2B + R*A + C = 0，(π1，π2，…，πm)B［R*］ =0，从而求解得出最小非负解R*，则稳态分布可以表示为：πk= πcR*k-c，k ≥ c，且 π 由方程组(π1，π2，…，πm)B［R*］ =唯一决定。

4 队列稳态性能指标

结合PH 分布的相关定义和性质，以矩阵论为模型求解基础，根据以往的通信网络系统排队的一般性指标定义，本文对下列通信网络排队的相关队列稳态性能指标进行求解：

(1)服务器平均服务时长

服务器服务时长是指同一服务器数次连续接收用户终端输入的平均工作时长，结合PH 分布的封闭性，则服务器服务时长也服从PH 分布，具有(φ，Q*)表示。

根据服务器平均服务时长的定义，可以得出MUB = -φQ*-1e。

(2)系统服务器平均占用率

系统服务器平均占用率是指系统服务器全部被占用的平均概率，根据系统状态转移矩阵Q 可得：

(3)服务器空闲稳态概率

服务器空闲稳态概率Pm是指m 个服务器至少有一个处于空闲状态的稳态概率，即系统稳态概率向量(π0，π1，π2，…，πn-1)：

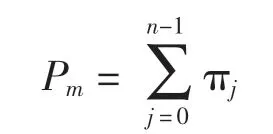
(4)用户终端平均队长

令Nf表示系统中等待的用户终端数量。根据系统稳态概率向量的含义，可以得出等待的用户终端数量的分布如下：

P{Nf= j} = πjj = n + 1，…，m

对其求期望可得出用户终端平均队长E［Nf］如下：

(5)稳态忙期服务器数量

令Nb表示处于忙期的服务器个数，则处于忙期的服务器的分布如下：

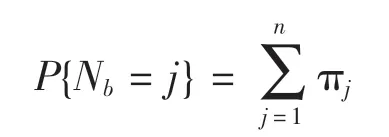
对其求期望可得出系统稳态忙期服务器数量E［Nb］如下：

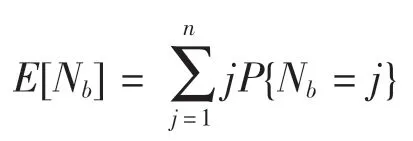
5 计算示例

假设有某小型有线通信网络系统，系统中有2个服务器和7 个用户终端，各服务器资源被占用时间和两用户终端到达服务器时间间隔均服从连续PH 分布，表示如下：

(1)服务器资源被占用时间：

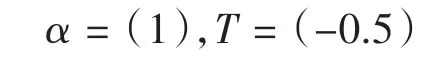
(2)两用户终端到达服务器时间间隔：

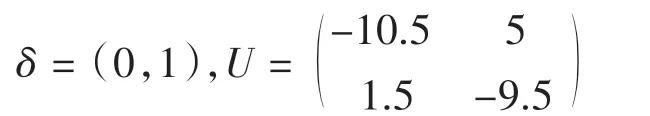
构建系统状态转移矩阵，对模型进行求解，可以得出：

服务器平均服务时长MUB = 0.963；

系统服务器占用率rz= 0.461；

服务器空闲稳态概率Pm= 0.134；

用户终端平均队长 E［Nf］ = 2.419；

稳态忙期服务器数量 E［Nb］ = 0.943。

通过对该示例结果进行分析，所得结果均符合有线通信网络M/M/C 排队模型相关指标要求，验证了模型对PH 分布的适用性和正确性，且具有优良的解析计算性。

6 小结

针对于小型通信网络组网服务器延迟服务的问题，引入排队论和PH 分布，利用排队论模型的计算公式及方法，可以确定用户终端排队系统的关键指标，如用户终端平均队长、服务器平均服务时长、系统服务器平均占用率等。综合考虑这些指标的影响以及系统建设成本和效益提升，可优化组网方案及有线通信服务机制，以有效提升综合效益。