露天煤矿两种常用土石方量计算方法对比研究

朱有彬

(北京天地华泰矿业管理股份有限公司，北京 100013)

在露天矿开采中，土石方剥离是最主要的生产环节，剥离土石方量的费用也是露天矿最大的生产成本。因此，精确计算土石方工程量不仅是工程预算、计算剥采比、编制煤矿的采剥计划和生产进度的依据，而且是采剥工程结算的基础[1-2]。但是在矿山的实际生产中，常遇到业主与承包商之间因为土石方量计算结果差异太大、超出合理误差允许范围的情况，最终导致工程款结算滞后。当前计算土石方量的方法相对较多，如方格网法、三角网法、断面法、平均高程法、等高线法等[3-6]，但各种计算方法的使用范围和条件一直没有明确的技术规范。为更好地服务于露天矿的生产，保证露天矿生产正常有序进行，有必要针对露天矿的土石方工程特征，对影响土石方量计算的相关因素进行研究分析。

本文以新疆准东地区某露天矿的土石方工程为实验数据，通过研究方格网法和三角网法这2种较常用的计算方法的计算原理、应用范围，并对比分析了在不同地形地貌条件、不同测点间距、不同方格网宽度等条件下方格网和三角网法分别对土方计算精度的影响，为露天矿精准计算土石方量提供了理论依据[7]。

1 土石方计算方法的原理分析

1.1 方格网法计算原理

方格网法是先把要测算的区域划分为一定边长的正方形网格[8]，由外业测量的原始地形地貌坐标点(x，y，z)得到正方形网格4个角上的原始高程值(若网格的角上没有高程点，可通过周围高程点内插得其高程)，再根据原始高程值设计高程作差，求出填挖线位置并绘制出填挖方分界线。然后根据网格边长和高程差值，求出每个网格的填挖方量，最后累计求和得出测算区的填方和挖方量[9-10]，其计算如图1所示[11-12]。

图1 方格网计算土石方量示意Fig.1 Calculation of earthwork by square grid method

方格网法计算公式见表1[11-12]。表1中，a为方格网的边长；b、c为零点到一角的边长；h1、h2、h3、h4为正方形方格网4个顶点的施工高程，代入它的绝对值；∑h为填挖方的高程总和；V为挖方或填方体积。把所有方形网格中的体积累加，即得到测算区域挖填方的总量。 由计算原理知，该方法操作简便，数据量较小，计算速度快，直观易懂，同时也不需要很大的数据存储空间[13-16]，且计算结果可手工复核，因此该方法在土石方施工工程中应用较为普遍。

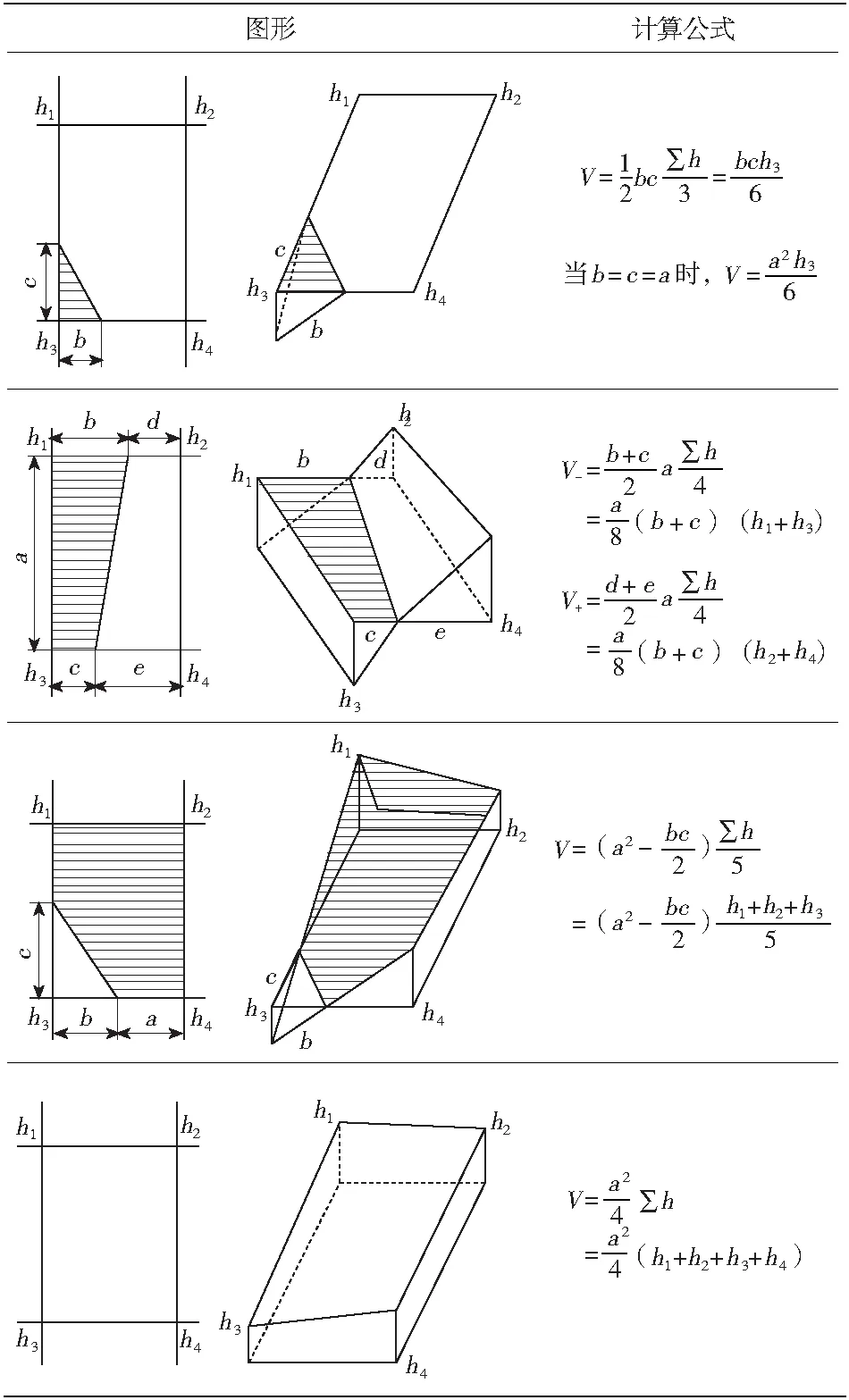
表1 方格网法计算公式Tab.1 The calculation formula by square grid

1.2 三角网法计算原理

三角网法就是根据施工前后实测的两期坐标(x，y，z)数据，构成邻接的等边三角形进而组合成不规则的三角网(TIN)，然后对需要计算的区域按照三棱柱的体积计算方法来计算，最后累计求和得出体积[17-18]。其公式如下：

(1)

式中，Vi为第i个三棱柱的体积；H1、H2、H3分别为三角形顶点填挖量；Si为三棱柱对应的投影底面积。

由于生成的不规则三角网能够充分还原实际的地形地貌，且不改变数据的精度[19]。因此，当测区的落差较大、计算范围不规则时，采用三角网(TIN)模型能够在很大程度上提升计算结果的精确度[20-21]。

三角网法计算土石方量如图2所示[7，22]。由计算原理知，该方法适应能力较强，无论是平坦的地形还是起伏较大、复杂多变、无规则的地形地貌，均可以有很好的适应性，它可以准确地模拟出原始的地形地貌特征[23-24]。但该方法所需数据较大，将占用较大的存储空间，在运算时又对计算机配置要求较高，且计算结果无法用手工核算[25]。

图2 三角网法计算土方示意Fig.2 Calculation of earthwork by triangulated network

2 工程案例

为定量研究2种土石方量计算方法的精度和对外业测量的要求，笔者以新疆准东地区某矿的两个土石方工程为试验数据，分别选取了测点间距在3、5、10、15 m外业测量数据，采用方格网法和三角网法进行土石方量计算，对比分析其计算结果精度。

2.1 实验区一

新疆准东地区某露天矿的生活福利区域要增建宿舍楼，在土建施工前需要进行平场处理，并计算平场中产生的土石方量。该区域地形地貌起伏变化不大，经计算需计算土方的面积为19 138.5 m2，场区最大高程为+704.49 m，最低高程为+704.08 m，场区内最大高差为0.41 m。平场施工前原始地貌数据作为起算底数据，并设定不变。平场后分别以3、5、10、15 m为外业测点间距对场区进行测量(测算区边界应测量完整[26-27])，其计算结果见表2。

由表2知：①采用三角网法计算，当测点间距在3～15 m时，其计算结果偏差为0～0.38%，由此得知测点间距对计算结果的影响较小。②采用方格网法计算，测点间距在3～15 m时，方格网的网格宽度从1 m到20 m逐渐增大时，计算结果的偏差(由0.14%增长到5.21%)也越来越大，网格宽度与偏差结果呈正向相关；当网格宽度不大于10 m时，计算结果偏差(0.02%～0.82%)不大。

表2 平坦地形的各种土石方量计算结果对比Tab.2 Comparison of the results of various earthwork calculation methods on flat landform

2.2 实验区二

新疆准东地区某露天矿采场内一区域的土石方工程，按照煤矿的采剥施工计划正常施工，然后计算采剥的土石方工程量。该区域地形地貌起伏较大，需计算土石方的面积为15691.5m2，最大高程为+769.78 m，最低高程为+757.23 m，最大高差为12.55 m，同样，以采剥施工前原始地貌数据作为起算底数据，并设定不变。采剥施工后，分别以3、5、10、15 m为外业测点间距对施工区进行测量(测算区边界应测量完整)，其计算结果见表3。由表3知：①外业测量的测点间距与计算结果偏差呈正向相关，即外业测量的测点间距越密，土石方量的计算结果越准确。②若采用三角网法计算，当测点间距在3～10 m时，计算结果偏差为0～0.44%；当测点间距为15 m时，计算结果的偏差达1.86%。③若采用方格网法计算，当方格网的网格宽度一定(以5 m×5 m网格为例)，测点间距从3 m到15 m变化时，计算结果的偏差(由2.15%增长到6.66%)越来越大，测点间距与偏差结果呈正向相关；当测点间距一定时(以5 m测点间距为例)，方格网的网格宽度从1 m到20 m变化时，计算结果的偏差(由2.20%增长到16.41%)也越来越大，网格宽度与偏差结果呈正向相关。

表3 复杂地形下各种土石方量计算结果对比Tab.3 Comparison of the results of various earthwork calculation methods on complex landform

《煤矿测量规程》中对露天矿土石方量的计算误差作出的规定为2次独立计算的体积误差不超过1.5%。但由于露天矿土石方的工程量较大，动辄千万方以上，1.5%的计算误差已不能满足实际计量的需求，某矿在采剥施工合同中约定，土石方量的计算误差为0.5%～1.0%。根据上述工程实例的计算结果对比分析(表2、表3)数据可知，若测区的地形地貌起伏不大，采用方格网法和三角网法均可满足土石方量计算的需求。若测区地形地貌比较复杂，当外业测量的测点间距不大于10 m时，采用三角网法计算土石方量能够满足精度要求，采用方格网法计算土石方量不能满足精度要求。

3 结论

(1)外业测量的测点间距与土石方量计算结果偏差呈正相关，即测点间距越密，土石方量的计算结果越接近实际值。若采用方格网法计算土石方量，当测点间距分别取3、5、10、15 m时，在地形地貌起伏不大的测区，计算结果偏差变化为0.14%～5.21%；在地形地貌比较复杂的测区，计算结果偏差变化为0.95%～16.41%，且方格网的网格宽度与计算结果偏差呈正相关，即网格的宽度越小，其计算结果偏差也越小。

(2)在地形地貌比较平坦的测区，可采用方格网法计算土石方量。综合外业测量的工作量和内业计算的难易程度，当选取测点间距10 m左右、网格宽度10 m，其土石方量计算结果精度可以控制在0.5%～1.0%。

(3)在地形地貌起伏较大的测区，宜采用三角网法计算土石方量。当测点间距在3～10 m时，计算结果偏差为0～0.44%；当测点间距为15 m时，计算结果的偏差达1.86%。在不过多增加外业测量工作量的条件下，测点间距一般5～10 m为宜。