页岩气临界吸附量的初步研究

马青华，张学梅，郝静远,2，李 东

(1.西安思源学院能源及化工大数据应用教学研究中心，陕西西安 710038；2.西安交通大学化工学院，陕西西安 710038)

页岩气产生并储存于页岩，是潜力巨大的非常规油气资源。众所周知，地表以下的固体都承受着水平应力和垂直应力，随着埋深而变化的应力以及它们的相对大小决定了受力固体的应变，而对岩体的孔隙、裂隙产生影响，进而影响到岩体的渗透和吸附。对页岩气吸附储量的正确评价是正确制定开发方案的基础[1-10]。

煤层气吸附量有临界深度以及相应的临界性质(压力、吸附量)，那么，页岩气吸附量是否有类似的临界深度以及相应的临界性质(压力、吸附量)呢？

“煤吸附气量—埋深关系图”[11]显示煤岩含气量随埋深先上升后下降，即煤层气吸附量随埋深的增加先上升，达到一个极大值，然后随着埋深的进一步增加却下降。在上升阶段，地层压力的正效应大于地层温度的负效应；在下降阶段，地层压力的正效应小于地层温度的负效应；在极大值(即拐点)时，地层压力的正效应等于地层温度的负效应。出现煤层气吸附极大值的深度被称为临界深度Hc，所对应的压力被定义为临界压力pc，所对应的吸附量被定义为临界吸附量Vc[1,11-13]。

本文以煤层气吸附量的临界性质为研究基础，选取了李武广[14]等、赵天逸[15]等、杨峰[16]等文章中的7个页岩样品，并将其文章中的系列等温吸附数据有效地转换为多元函数(温度—压力—吸附)方程。通过对4个临界值，即“临界深度Hc”“临界压力pc”“临界吸附量Vc”和“临界温度Tc”相应的数值模拟计算，探讨页岩气出现吸附极大值的条件及因素。

1 页岩样品

由于没有实测数据，故从参考文献里选择李武广[14]等的T-1、T-2、R-1、R-2 4个样品，赵天逸[15]等的T-1、Alum 2个样品，以及杨峰[16]等的一个黑色页岩样品。因为李武广[14]等和赵天逸[15]等6个页岩样品在各自的原文中都用“T-1”作为标识，所以按原文第一作者的姓而分别标识为“李T-1”和“赵T-1”。

页岩样品均使用常规系列等温吸附数据，即7种页岩岩心在不同温度下的兰氏吸附体积和兰氏压力。7个页岩样品中的4个在4个温度下进行试验，其余3个在3个温度下进行试验。样品数据均由相应文章作者经过实验所得，实验原理清楚，过程科学严谨；数据分析在合理区间，流程正确。其他的页岩性质因与本文研究内容无关而并未引用，但可到原文中查找。

表1 7种页岩岩心在不同温度下的兰氏吸附体积和兰氏压力[14-16]

2 温度—压力—吸附方程及数据处理

2.1 温度—压力—吸附方程

温度—压力—吸附方程(Temperature-Pressure-Adsorption Equation, TPAE)是包含温度、压力和吸附体积3个相互共存、互为影响变量的数学方程，旨在研究指定温度和气体压力下煤的吸附量变化的函数关系[17-19]。

(1)

式中A——一个固定的多孔介质的微孔几何形体常数，是与努尔森扩散有关的参数，无量纲；

B——吸附流量系数，与吸附区域相关，无量纲；

M——分子量，甲烷的分子量为16；

p——压力，MPa；

T——绝对温度，K；

V——吸附量，cm3/g；

β——衡量吸附压力的相对影响的参数，无量纲；

2.2 数据处理

页岩的系列等温吸附数据是以兰氏体积和兰氏压力的方式加以报道。要想求得温度—压力—吸附方程的参数，只能先将各页岩样品的兰氏体积和兰氏压力转换成相应温度、压力下的吸附量，并由这些不同温度、压力下的吸附量回归计算温度—压力—吸附方程的参数。已有文章以陕西焦坪崔家沟7号煤为例[20]，详细分步说明了如何利用系列等温吸附的兰氏体积和兰氏压力建立回归样本集、确定温度—压力—吸附方程的4个参数，以及计算相对平均误差。页岩也按相同的方法步骤进行，在此就不一一重复。7个页岩样品的相应参数列于表2：

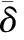
表2 7种页岩岩心在测试温度内的相应参数和平均相对误差

只对压力的上、下限和间隔补充说明两点：

(1)对于每个测试温度，压力下限为1.0 MPa，上限为10.0 MPa，间隔为1.0 MPa，共计10个压力测试点。因此，如果页岩样品有4个测试温度，那么相对平均误差就是40个相对误差的平均值；如果页岩样品有3个测试温度，那么相对平均误差就是30个相对误差的平均值。

(2)A与努尔森扩散有关，是一个表征多孔介质的微孔几何形体常数[21]。对于所研究的页岩，A值恒等于0.05。

2.3 页岩气的吸附极值计算

要想对温度—压力—吸附方程这样一个多元函数方程求极值，必须用到其全微分。在A相对较小而被忽略时，温度—压力—吸附方程的一阶全微分为：

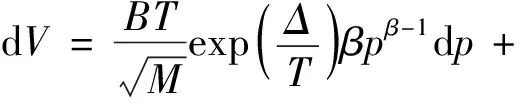
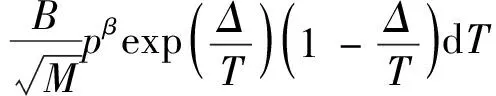
(2)

在变温变压条件下，吸附量出现极大值的必要条件是全微分等于零。将该全微分等于零的齐次方程整理、移项后可得：

(3)

该简化后的齐次方程有2个已知量(β、)和4个未知量(T、p、dT、dp)。显然用一个方程是不可能解4个未知数的。但是可以利用勘探页岩并取样时所测定的3个数据来消除3个未知量来进一步简化方程，即：

(1)测定的地温梯度，如3 ℃/100 m时，dT=3；

(2)测定的地压梯度，如1 MPa/100 m时，dp=1；

(3)测定的恒温层温度，如15 ℃为恒温层温度时，T=15+3p+273。

由此，方程(3)就成为一个以压力p(单位为MPa)为未知数的一元二次方程。从数学上分析，一元二次方程有实数解的充分条件是该一元二次方程的判别式大于或等于零，当一元二次方程的判别式大于零时有两个不同的实数解，当一元二次方程的判别式等于零时就只有一个实数解。

3 结果与讨论

(1)与煤层气吸附一样，页岩吸附极大值是客观存在的。其必要条件是描述该页岩吸附的温度—压力—吸附方程的一阶全微分为零。而该页岩吸附的温度—压力—吸附方程的参数是可以用页岩的系列等温吸附数据来求得。

(2)求临界深度Hc：

(4)

式中a1、a2、a3、a4、a5、a6——待定系数；

Ro,max——镜质组最大发射率。

当地温梯度dT、压力梯度dp和恒温地层温度Th(K)值确定后，这些待定系数则确定。

(3)求临界压力pc：

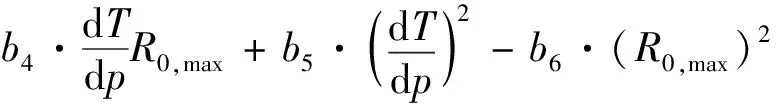
(5)

式中b1、b2、b3、b4、b5、b6——待定系数。

当地温梯度dT、压力梯度dp和恒温地层温度Th(K)值确定后，这些待定系数则确定。

(4)求临界吸附量Vc：

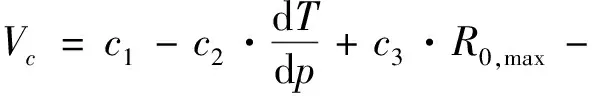
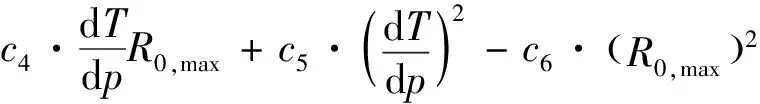
(6)

式中c1、c2、c3、c4、c5、c6——待定系数。

当地温梯度dT、压力梯度dp和恒温地层温度Th(K)值确定后，这些待定系数则确定。

(5)存在页岩吸附极大值必要且充分的条件是该一元二次方程的判别式大于或等于零。表3列出计算7个页岩样品吸附极大值的结果。

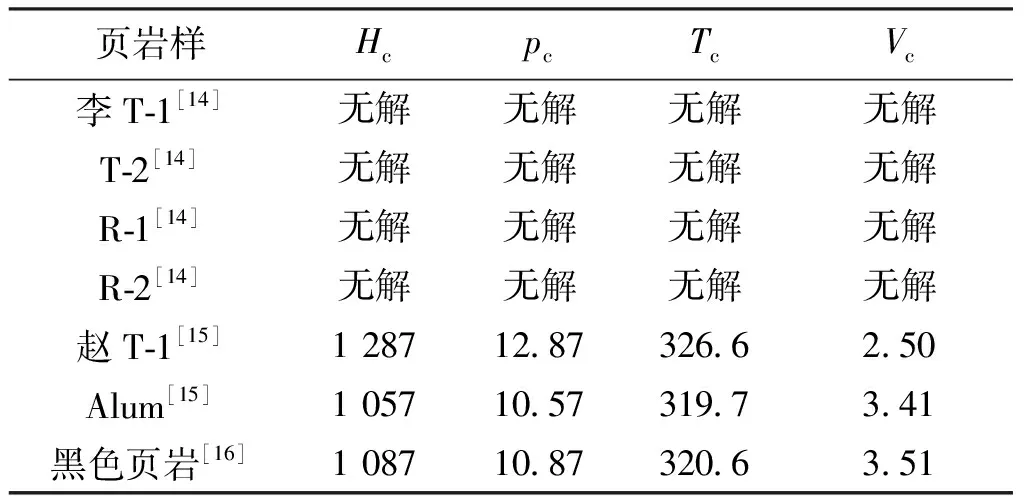
表3 7个页岩样吸附极大值的计算结果

表3的计算结果是按3点假设：①地温梯度为3 ℃/100 m；②地压梯度为1 MPa/100 m；③恒温层温度为15 ℃。

如果取页岩样品的地温梯度、地压梯度和恒温层温度与上述的假设有一点不同，那么所得到的临界深度会有不同，甚至可能出现完全不同的结果，如原来有吸附极大值的变成没有极大值，而原来没有吸附极大值的变成有极大值。

(6)地层温度负效应和地层压力正效应的比值。

按地应力状态的转换理论，任何页岩都应该有极值，没有例外。而通过温度—压力—吸附方程求页岩气吸附极大值的必要且充分的条件则解释在什么条件下，页岩气吸附出现极大值；在什么条件下，尽管有地层压力正效应和地层温度负效应，但页岩气吸附不会出现极大值。为此，特别定义一个衡量温度效应与压力效应之比的参数/β，称之为“温压比”。可见温压比是个分数，而使分数变大有3种途径：①分子变大；②分母变小；③分子变大和分母变小。表4列出了7个页岩样品的温压比和相应的吸附极大值。

表4 7个页岩样品的温压比和相应吸附极大值

(7)尽管页岩一般较煤岩埋藏更深，但页岩气和煤层气一样具有游离相态、吸附相态和溶解相态为其赋存相态，所以这两种气井都采取排水降压的方式生产气体。从概念上了解，自变量单向变化(压力单调下降)对因变量(吸附量)在极大值(临界深度所对应的临界压力)附近的影响是很重要的。换句话说，当气井的目标深度是在临界深度以深，采取排水降压的方式生产气体会先随压力降低而含气量增高，达到一个最大值后，随压力降低而含气量降低，直至需要清洗、修补、恢复和提高。当气井的目标深度是在临界深度以浅，采取排水降压的方式生产气体会随压力降低而含气量就会降低，直至需要清洗、修补、恢复和提高。

4 结论

(1)可以将页岩的系列等温吸附数据有效地转换为多元函数(温度—压力—吸附)方程。7个页岩样品转换后的相对平均误差仅在4.46%～6.61%之间。

(2)页岩气吸附出现极大值的必要条件是温度—压力—吸附方程的一阶全微分为零。

(3)页岩气吸附出现极大值的充分条件是通过简化温度—压力—吸附方程一阶全微分得到的一元二次方程的特征判别式大于和等于零。

(4)特别定义“温压比”来衡量温度效应与压力效应之比的参数/β。温压比大于3 340的3个页岩样品出现吸附极大值，而温压比小于1 820的4个页岩样品没有出现吸附极大值。