一种新的飞航导弹飞行高度测量处理方法
高 冰 何林泽
(中国人民解放军92941 部队,辽宁葫芦岛125001)
1 引 言
飞航型号反舰导弹其掠海飞行高度是体现导弹战术技术性能的一项重要指标,特别是超低空掠海飞行能力是提高导弹突防能力的重要手段[1]。一般的导弹防御系统对付超低空、“擦树梢”、掠海、机动多变飞行、低成本、群体作战的飞航导弹往往是无能为力和得不偿失的[2]。所以,在飞航型号反舰导弹试验中,对其飞行高度的测量和处理精度有很高要求,特别是在弹上高度表精度已达到米级的情况下[3,4],对飞行高度的测量精度应优于米级。相应地,近年来新一代舰空型号导弹,对其超低空拦截性能的考核也是一项重要的战技指标,因此对预拦截的靶弹供靶高度的精度也提出米级的要求[5]。
在高度测量上,因受大气折射影响,误差甚至超过10m 以上。测量设备距离目标越远,俯仰角越低时,大气折射带来的误差越大,尤其是对超低空飞航型号导弹,大气折射引起的测角系统误差和测距系统误更大。当目标相对于测量设备为低负仰角时,大气折射给高低角带来的测量误差最大可达3′~4′,高度方向上大气折射有时引起的误差可达20m[6]。常规的大气折射修正方法,只适用于高仰角,利用常规方法对低负仰角进行折射修正,其修正剩余误差会越来越大。根据大气折射修正的经验,在大气状态稳定的情况下,气象测量参数精度较高,经大气折射处理出的目标高度精度也较高,但当大气状态变化剧烈,气象测量结果误差较大时,大气折射修正残差将达到1′以上,带来的高度折射残差大于(3 ~5)m[7]。针对这种问题,本文提出航区等高参照物误差折算的飞航导弹海面高计算方法。
2 基本思路
在飞行航路附近特定载体上设定多个参照目标,通过精测手段测得这些参照物的高度,将其作为真值,对测量系统相对这些参照物的测量数据进行修正,获得其在航路上的测量误差,利用其修正飞航导弹飞行高度测量数据,以获取满足精度要求的导弹海面高数据。
在发射平台和沿航区布设的多条巡逻艇上加装光学合作目标。具体安装要求是在发射平台两端各加装2 个曳光管,并加装GPS 测量系统;同时在各巡逻艇上一侧特定位置上安装曳光管并加装GPS 测量系统,曳光管与GPS 接收机天线安装高度尽量接近,曳光管安装位置应保证光学经纬仪正常测量。
导弹发射后接力点燃发射平台两端曳光管及巡逻艇上的曳光管,并同时测量飞行的导弹和经过的曳光管;导弹飞行结束后,再次接力点燃发射平台两端曳光管及巡逻艇上的曳光管,光学经纬仪进行跟踪测量;发射平台和巡逻艇上的GPS 全程进行测量。
试验前,利用激光测距等高精度手段测量发射平台、巡逻艇上曳光管和GPS 接收机天线距海面高度;试验结束后,对光学经纬仪获取的导弹、发射平台和巡逻艇上曳光管测量数据按同一流程进行处理,计算出发射平台和各巡逻艇上曳光管测量结果中高度数据的系统误差值,利用此系统误差值对导弹飞行高度测量结果进行修正,以提高数据精度。
3 计算飞航导弹海面高的新方法
3.1 高度计算方法的选择
利用光学经纬仪测量数据计算目标高度有双站交会和多站数据融合处理两种方法[8]。光学经纬仪双站交会法处理环节少,处理效率高,可作为快速分析的主要数据来源,但是误差模型和数据处理方法简单,结果精度较低。多站数据融合处理方法和误差模型合理,结果精度通常比双站交会数据处理方法高一个量级,但是处理过程复杂、环节多、周期长。为满足飞航导弹掠海飞行高度的高精度试验要求,显然在外场测量设备能够提供大量有效测量数据的前提下,应尽量选择采用多站数据融合处理方法。
3.2 航区等高参照物高度系统误差折算方法依据
不同高度大气参数的变化为:高度升高1km,温度下降6℃;水平方向变化无规律,但从国内气象资料中可以查得,100km 范围内温差小于2℃,湿度差不超过2%。可认为在水平方向近距离10km 内海面上两点的大气环境是相同的,大气折射误差基本是一致的。因此采用航区等高参照物误差折算方法计算飞航导弹海面高是可行的。
3.3 航区等高参照物高度系统误差计算方法和步骤
根据上面的分析,提出航区等高参照物系统误差测量与处理方法,该方法步骤如下。
1)在导弹等被测目标附近,一般约(5 ~10)km,距离发射平台和巡逻艇上布设曳光管等参照目标,由布设人员在平台上采取精测手段近距离测量该参照目标距海面的真实高度Hz;
2)试验零点前光测系统首先对发射平台和巡逻艇曳光管等参照目标进行测量,事后处理得到该参照目标大地高度Hc1,此时参照目标高度Hc1含有测量系统误差、大气折射误差、潮汐、高程异常及各种不易模型化的误差,计算公式为
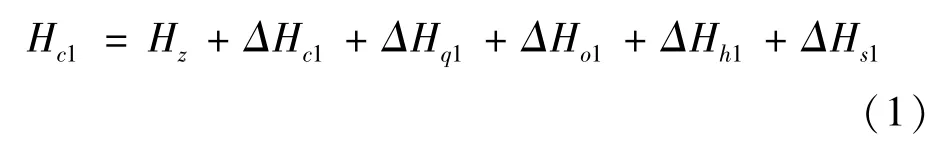
式中:Hc1——试验零点前参照目标大地高度;Hz——参照目标距海面高度真值;ΔHc1——试验零点前参照目标海面高度测量误差;ΔHq1——试验零点前参照目标高度大气折射误差;ΔHo1——试验零点前参照目标潮高;ΔHh1——试验零点前参照目标当地高程异常值;ΔHs1——试验零点前参照目标高度方向上不易模型化的误差。
3)在试验结束后光测系统再次对参照目标进行测量,事后处理得到参照目标大地高度Hc2,显然参照目标高度Hc2也含有测量系统误差、大气折射误差、潮汐、高程异常及各种不易模型化的误差,计算公式为

式中:Hc2——试验零点后参照目标大地高度;ΔHc2——试验零点后参照目标高度测量误差;ΔHq2——试验零点后参照目标高度大气折射误差;ΔHo2——试验零点后参照目标潮高;ΔHh2——参照目标当地高程异常值;ΔHs2——试验零点后参照目标高度方向上不易模型化的误差。
4)取Hc1和Hc2的平均值得到¯Hc
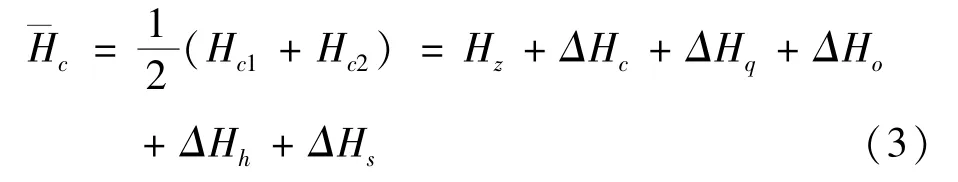
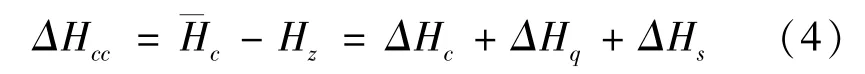
式中:ΔHcc——试验零点前后对参照物目标高度测量修正误差。
此时对参照目标高度的测量修正误差ΔHcc仅含有测量误差ΔHc、大气折射误差ΔHq及误差ΔHs。
3.4 飞航导弹海面高精确计算方法
试验结束后对获取的导弹飞行测量数据进行处理,得到导弹飞行大地高度hc,此时导弹飞行海面高hz可表示为

式中:hz——期望获得的高精度导弹距海面高度;hc——试验中导弹飞行的大地高度;Δhc——对导弹飞行高度测量误差、Δhq——导弹高度大气折射误差;Δho——导弹飞行航路上潮高(相对平均海平面);Δhh——飞行航路上高程异常值;Δhs——导弹高度方向上不易模型化的误差。
在导弹与参照目标距离较小,一般为(5 ~10)km,且在光学经纬仪同一画幅条件下,基本满足:ΔHc≈Δhc,ΔHq≈Δhq,ΔHo≈Δho,ΔHh≈Δhh,ΔHs≈Δhs。
由式(5)可得

ΔHcc由对参照目标测量处理得到,ΔHo由当地验潮站提供,ΔHh由航保部门提供。上述计算得到的hz即为期望获得的高精度导弹掠海飞行海面高度。
3.5 飞航导弹海面高精确计算流程
1)对获取的光学原始数据进行直接处理,可计算得到导弹飞行大地高hc
此时,该高度含有测量系统误差、大气折射误差、潮汐、高程异常及各种不易模型化的误差。
2)计算导弹飞行海拔高hhb

此时,该高度结果修正了高程异常的影响。
3)计算导弹飞行海面高初值h′z
设试验海区潮高基准面高度为H0(验潮站提供),飞行时刻t瞬时潮高为Hot(潮汐表查取),则导弹海面高初值h′z为

此时,该高度结果修正了瞬时潮汐的影响,但仍含有大气折射误差和不易模型化的其误差。
4)海面高修正
设参照物(发射平台或巡逻艇上曳光管)海面高为Hz,试验前后光学经纬仪测得参照物(发射平台或巡逻艇上曳光管)海面高度均值为¯Hc,则海面高测量误差修正值为ΔHcc。
将由式(8)计算得到的导弹海面飞行高度初值h′z,通过ΔHcc进行误差修正后,处理得到满足精度要求的导弹掠海飞行海面高度hz为

4 精度分析
4.1 系统误差影响
经纬仪测量系统误差在一次试验过程中通常是稳定的,对于导弹尾部的曳光管、发射平台和巡逻艇上的曳光管的测量,由于目标特性一致,故测量成像和判读部位是一致的,即测量装备系统误差是一致的,所需考虑的主要是随机误差。
高程异常是大地椭球面和大地水准面之差,通过常规大地测量提供的高程异常值修正结果,使高程异常修正精度可达到要求。
当天的潮汐数据是由验潮站常年测量得到的潮汐统计值,针对试验当天的气候特点,潮汐存在一定的误差,瞬时验潮结果精度可达到要求。
其它不易模型化的误差项,如站址误差、时统不同步误差、判读误差等影响较小,且对同一画幅的两个目标的影响具有一致性,均可通过一次差修正。
4.2 随机误差影响
由于测量方案设计中采用了相对修正的处理方法,因此系统误差将被大大消除,对处理结果精度影响最大的因素是随机误差。
光学经纬仪是试验中常用弹道测量装备,通过采用平滑滤波、多项式拟合等方法,基本可消除随机误差影响。
采用多站数据融合处理方法,测量装备随机误差对导弹飞行高度计算结果的精度影响可优化达到试验的精度要求。
4.3 精度估算
通过上述的误差分析,对经过各种误差修正的导弹飞行高度的精度估算结果为

式中:σc——测量设备均方根误差;σq为大气测量均方根误差;σh——大地测量均方根误差;σo——潮高测量均方根误差;σs——随机误差均方根误差。
通过精度分析,采用上述测量方案和数据处理方法,最后得到的飞航导弹海面高度精度满足要求。
4.4 工程应用数据分析
在某型光电经纬仪精度试验中,海上有两个巡逻艇,相距5.7km,巡逻艇A 布设了一个曳光管作为参照目标,巡逻艇B 布设的曳光管是被测目标,曳光管距水面真实高度为8.7m,应用本文方法和传统大气折射误差修正方法对被测目标进行了计算,结果如图1 至图3 所示。
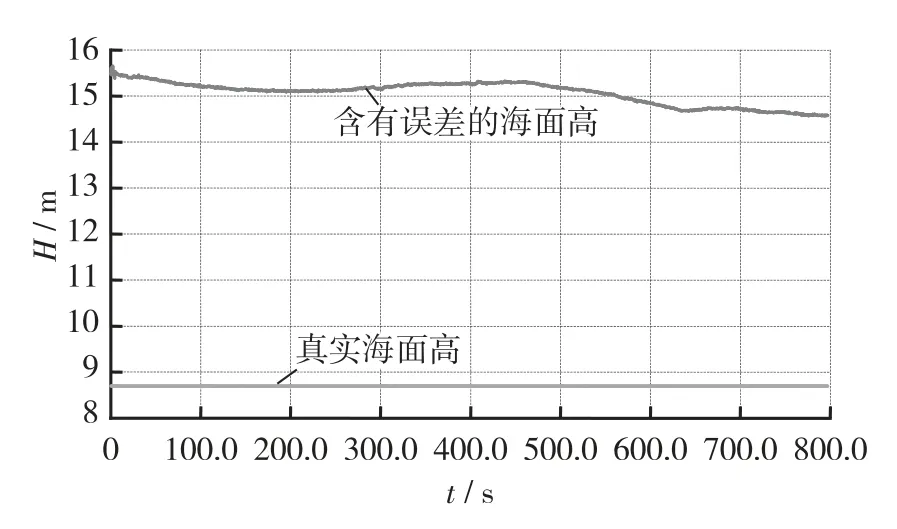
图1 巡逻艇A 含有误差的海面高和系统误差图Fig.1 Height above sea level with errors of the patrol boat A and systematic errors

图2 高度系统误差图Fig.2 Systematic errors of height

图3 巡逻艇B 海面高图Fig.3 Height above sea level of the patrol b`oat
从图1 可以看出,高度数据有(6 ~7)m 的误差,显然大大超过飞航导弹对高度精度的要求。从图2 可以看出系统误差最大值和最小值在1m 之内,其结果验证了本文提出的航区等高参照物系统误差折算方法的思路是合理的。图3 是分别采用传统的大气折射修正和本文方法计算得到的被测目标海面高与真值的对比图,显然,本文方法计算得到的目标海面高更接近真值。在该次精度试验中本文方法在高度上精度比传统大气折射修正方法提高了近2m,与真值误差在1m 以内。
5 结束语
采取相对修正思路,在航路附近固定位置设置参照物,事先通过精测手段获得参照物高度;之后测量设备同时获取参照物和待测目标数据,以通过对参照物两种情况下测量得到的系统误差修正飞行目标系统误差,这种修正方法不通过传统大气折射修正来实现。从工程应用结果来看,文中提出的掠海型飞航导弹海面高精确测量与处理方法,设计合理,处理结果精度高,实施步骤简单,参照物容易布设,在工程上有一定的应用价值。

