一种基于DOA和TOA的水声脉冲信号被动测距方法

罗浚 柏祥华 安良

（1.东南大学水声信号处理教育部重点实验室，南京，210096）

（2.海装上海局驻南京地区第一军事代表室，南京，210000）

水声被动测距是水声信号处理和水声对抗领域的难点之一[1]，面临着信号形式、频率、DOA、时间等先验信息缺失问题。尤其是水声脉冲信号的被动定位，由于水声脉冲信号是间歇式发射的非合作水声信号，无法通过长时间的积分获得时间增益。信号占空比较大，导致所获取的数据量相对于辐射噪声等信号较少，这也加大了脉冲信号被动测距的难度。目前，未知参量脉冲信号被动测距有三类方法：三元阵测距、匹配场处理和目标运动分析（Target Motion Analysis，TMA）[2]。对于三元阵测距，水声信道的复杂性导致传播时延起伏，实现多水听器布阵也较为困难。匹配场处理的测距性能对海洋声学参数的预估精度要求很高，如果参数失配则无法实现定位。因此，在已知系统的状态模型与观测模型的前提下，采用TMA是较为有效的被动定位方法[3]。

经典的TMA被动定位方法分为纯方位TMA、方位-信号到达时间差TMA等。前者需要观测站机动，因此具有很大的局限性[4]；后者充分利用DOA与 TOA作为观测量建立模型，使得该方法不需要观测站机动。在非线性系统中，经常使用EKF方法进行跟踪，通过保留系统泰勒展开式的一阶项、省略高阶项的方法得到近似线性化的系统，该方法必定会产生误差，且误差会随着样本数量累积，可能会导致滤波器发散[5]。基于Unscented变换的UKF方法没有忽略系统高阶项，而是通过一系列的采样点获取随机变量的均值和方差[6]。当状态变量通过实际的非线性系统之后，后验均值与协方差估计值可精确至三阶，进而改善系统的计算精度与非线性效果[7-8]。

海洋水声环境十分复杂，多途传播、阵形畸变都是不可避免的，这些对声信号传播的影响很大[9]。这使得用于声源定位的方位、信号到达时间差等参数估计误差较电磁信号源大，导致用于电磁信号源定位的传统TMA方法进行水声信号跟踪时，结果容易发散、系统性能下降。

本文提出基于DOA与TOA的MAF-PLE-UKF联合方法，首先使用MAF方法对用于初值估计的DOA和TOA观测数据进行平滑预处理，之后使用PLE方法估计目标状态初值，再使用UKF对目标信息进行跟踪，以提高目标跟踪的收敛性能和定位精度。

1 定位模型建立

1.1 目标状态模型

假设观测站固定不动，以观测站为原点，正东方向为x轴、正北方向为y轴建立直角坐标系。目标按照某一未知方向做匀速直线运动，并发射周期恒定的脉冲信号，如图1所示。

图1 目标与观测站的运动几何关系的模型

记初始时刻为0时刻，令tk表示第k时刻，则目标在第k时刻的状态矢量为

式中，xk、yk为目标第k时刻的位置，Tr为目标发射脉冲的周期，dx、dy为目标在Tr时间内沿x、y轴方向的位移。系统下一时刻的状态方程为

式中，Wk表示系统噪声，假设其服从高斯分布，其协方差矩阵记为Qk。Φ(k+1/k)表示系统状态矩阵：

1.2 目标观测模型

观测站进行第k次观测时，目标的角度βk与相邻脉冲的到达时间差ΔTk分别为

根据式（3）、（4），可将观测模型表达式记为

式中，nk为观测误差矩阵，其协方差矩阵记为Rk。

2 定位方法原理

2.1 滑动平均滤波法进行数据预处理

针对水声脉冲参数估计误差较大的问题，首先使用滑动平均滤波法对用于状态初值估计的脉冲DOA与TOA观测数据进行平滑处理。该方法的基本思想是：一个时间点的取值由当前时间点及其邻域内时间点的平均值来代替[10]。通常是使用一个滤波窗实现的，设窗长为M。在时间点tk时，窗口选中的时间区域为St，输入数据为g(n)，则该时间点滤波器的输出f(tk)为

选取窗长为5个时间点，使用滑动平均滤波法，对DOA和TOA观测数据进行预处理。

2.2 伪线性方法估计初值

实际应用中，UKF方法对初始值的准确性较为敏感。在没有水声脉冲参数先验信息的情况下，本模型采用伪线性方法对初值进行估计。对于第k次观测，根据坐标的几何关系，可将（3）、（4）式转化为线性表示形式：

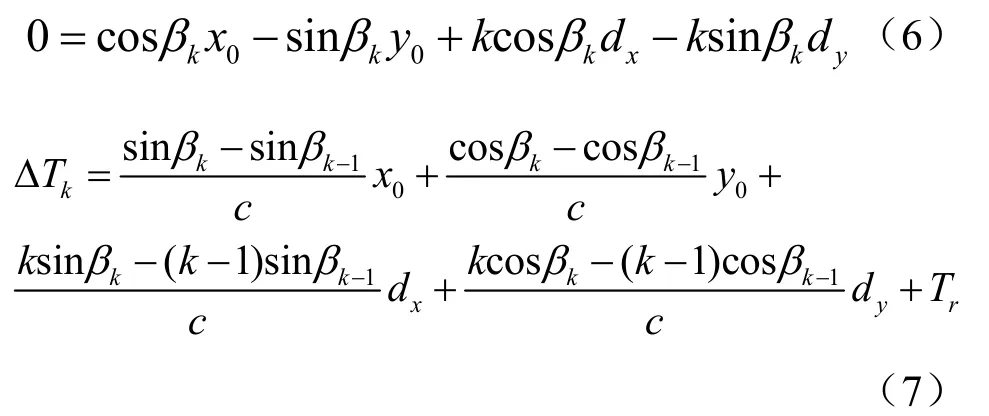
假设含有噪声的观测量为βmk、ΔTmk，它们与真实值βk、ΔTk的关系为

其中，nβk与nΔTk分别表示方位、脉冲到达时间差的估计误差，并服从均值为零的高斯分布。将观测关系式（8）、（9）代入线性化的关系式（6）、（7）中。在噪声较小，并且观测目标距离观测站较远时，可做式（10）～（13）的近似：

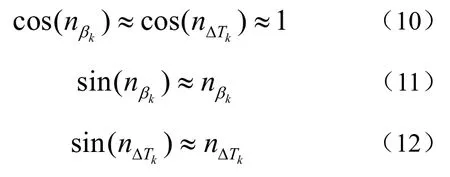
对公式进行计算与整理可得到，系统线性观测方程的等效角度与脉冲到达时间差的测量噪声为rknβk与nΔTk（rk表示k时刻目标与观测站间的距离）。记系统观测方程的等效噪声Nk为

由此便可将观测模型表达式（5）表示为线性形式：

对于每一时刻tk，根据式（14），观测方程都可表示为矩阵形式：

式中，对角度βk与脉冲到达时间差ΔTk的测量是相互独立的，方差为。由此可得Nk的协方差矩阵Rk为

经过N次观测后，线性观测方程表示为

对初始状态量X0的加权最小二乘估计[11]：

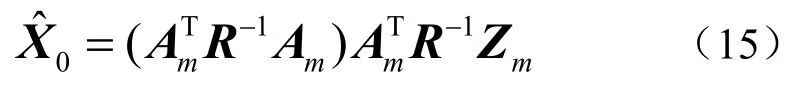
式中，该算法需要预先设定矩阵R的值进行计算。0为伪线性估计的系统状态初值。

2.3 无迹卡尔曼滤波方法定位与跟踪

获得估计的初值后，使用无迹卡尔曼滤波方法对目标状态进行跟踪。UKF以Unscented变换为基础[12]。Unscented变换根据系统状态向量x的维数n，选取2n+1个近似高斯分布的Sigma点，均值为系统状态量均值，方差为系统协方差P[13]。通过这组Sigma点对系统状态向量的概率密度函数进行近似化，而不是对系统的非线性函数进行近似线性化，从而克服了线性化所带来的滤波误差[14]。

在第k+1次观测时，基于DOA与TOA的UKF算法的具体计算步骤如下：

（1）首先根据k时刻的状态估计量(k/k)、系统估计协方差P(k/k)以及Unscented变换的原理，求得最初的2n+1个Sigma点。将Sigma点组成的向量记为Ei(k/k)，相应的权值记为和，上标m与均值相对应，上标c与方差相对应。其中i为从1～2n+1的值。Sigma向量和采样权重的取值分别为

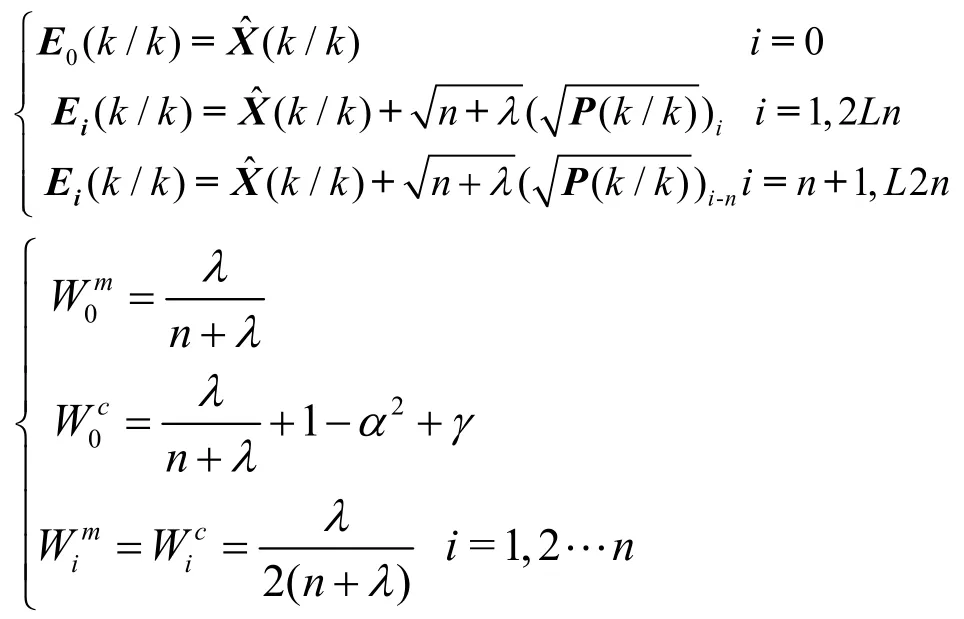
（2）将系统的状态方程（1）式记为f，求得Sigma点的预测值Ei(k+1/k)，预测值的估计(k+1/k)和预测值的协方差P(k+1/k)为

（3）根据系统的观测方程（5）式，计算观测值Zi(k+1/k)，并计算观测值的估计(k+1/k)和协方差Pzz(k+1/k)：

（4）计算Ei(k+1/k)、Zi(k+1/k)的协方差Pxz(k+1/k)与系统的卡尔曼增益G(k+1)：

（5）进行协方差P(k+1/k+1)和系统状态(k+1/k+1)的更新：

由此便完成对k+1时刻状态方程的估计。

3 仿真结果与分析

假设观测站静止于坐标原点，目标真实的初始状态位置x0为22 km，y0为16 km。目标发射周期Tr为30 s的脉冲信号；其在一个脉冲周期内的位移dx为-150 m，dy为60 m，其中系统位置噪声标准差σrx与σry为1 m，一个脉冲周期内系统位移的噪声标准差σdx与σdy为0.1 m。观测器每隔1个脉冲周期测得一组角度与相邻脉冲到达时间差的数据。使用300组观测数据进行仿真。

对于水声脉冲信号的DOA估计，近代声呐的测向精度为0.25°～1°[15]。对于水声脉冲信号的TOA估计，可使用短时傅里叶变换等时频分析方法对接收的信号进行处理得到。该方法的估计精度为窗函数的移动步长，可选取为脉冲信号脉宽的百分之一[16]，通常水声脉冲信号脉宽为毫秒级至秒级，因此TOA观测噪声参数可选取毫秒级进行仿真。本次仿真选取角度观测噪声标准差σβ为1°，相邻脉冲到达时间差噪声标准差σΔT为5 ms。

在进行PLE估计时，矩阵R初值的选择将影响估计的性能。由于没有先验信息，σβ、σΔT、rk这3个参数的真值是未知的，因此首先通过仿真分析矩阵R初值选择对距离估计的影响。图2～4为这3个参数取不同初值时PLE距离估计相对误差曲线，仿真过程中σβ真值为 1°、σΔT真值为 5 ms、rk真值为27 km。在进行PLE距离估计时，依次改变其中1个参数的取值，另外两个参数均取真实值，构造R矩阵。每个参数改变时的Monte-Carlo仿真次数均为100次。

对比图2～4的结果可知，σβ与rk取不同初值时，距离估计相对误差变化不大；而距离估计相对误差对σΔT初值的选择较为敏感。在之后的伪线性估计仿真中，协方差矩阵R的初值设定时，参数σβ取为1.5°；σΔT取为 6 ms；距离rk设定为 81 km。

图2 不同DOA标准差时的PLE距离估计相对误差

图3 不同TOA标准差时的PLE距离估计相对误差

图4 不同距离初值时的PLE距离估计相对误差

图5和图6为伪线性距离初值估计误差百分比的区间分布。图5为未使用滑动平均滤波法对脉冲参数进行预处理后的估计结果，图6为使用参数预处理的结果，Monte-Carlo仿真次数为100次。

图5 未进行平滑预处理的预测初始距离与实际距离的比值分布情况

图6 进行平滑预处理后的预测初始距离与实际距离的比值分布情况

对比图 5、6可见，未进行参数预处理时，仅15%比例数据的距离估计误差低于30%；进行参数预处理后，66%比例数据的距离估计误差低于30%。使用滑动平均滤波法进行数据预处理，可以减小伪线性初始距离估计的误差。

改变用于PLE初值估计的组数，对比进行数据平滑处理前后系统跟踪的收敛率变化情况，如表 1所示。从表中可知，不进行平滑预处理时，至少需要30组观测数据进行PLE估计才能达到90%以上的收敛率；而进行平滑预处理后，利用 20组观测数据即可达到 90%以上的收敛率。因此选取前 20组数据进行PLE初值估计。

表1 系统跟踪收敛率与初值选取组数的关系

若N为Monte-Carlo仿真次数，卡尔曼滤波器距离估计的均方根误差（RMSE）为

系统状态量Xk跟踪精度的克拉美罗下界（CRLB）的公式为

公式详细推导参见文献[11]。

为了对比不同方法距离估计的性能，根据对系统状态量Xk估计的CRLB，可选取距离估计误差参考值为[17]：

式中，CRLBk(1,1)和CRLBk(2,2)分别为系统状态量xk、yk的CRLB值。

图7为UKF与MAF-PLE-UKF方法距离估计的RMSE对比图。UKF通过空间几何三点法估计目标初始位置[18]。100次Monte-Carlo仿真中，UKF收敛率为 74%，而 MAF-PLE-UKF方法收敛率为93%，较 UKF提升了 19%收敛率，且 MAF-PLEUKF方法的距离估计性能也明显优于UKF。

图7 UKF与MAF-PLE-UKF方法距离估计的RMSE对比图

图8～9分别为MAF平滑预处理前后PLE-UKF与 PLE-EKF算法的距离估计性能对比图。由于选取了前20组数据进行PLE初值估计，因此从第21组进行系统测距的性能分析。

图8 未进行数据平滑处理的PLE-EKF方法与PLE-UKF方法距离估计的RMSE对比图

图9 进行数据平滑处理后的PLE-EKF方法与PLE-UKF方法距离估计的RMSE对比图

图8为未进行数据平滑处理的情况。在第100组时，rek为 626.3 m，PLE-EKF求得的距离估计RMSE为 2048 m，而 PLE-UKF求得的距离估计RMSE为1111 m。在第200组时，rek为337.1 m，PLE-EKF求得的距离估计RMSE为 826.8 m，而PLE-UKF求得的距离估计RMSE为475.7 m。在收敛率方面，PLE-EKF收敛率为63%，而PLE-UKF收敛率为 77%。在未进行数据平滑处理时，PLE-UKF收敛性能明显优于 PLE-EKF，有更好的宽容性。

图9为进行MAF平滑预处理后的情况。在第100组时，rek为626.3 m，PLE-EKF求得的距离估计RMSE为1318 m，而PLE-UKF求得的距离估计RMSE为938.6 m。在第200组时，rek为337.1 m，PLE-EKF求得的距离估计RMSE为 506.3 m，而PLE-UKF求得的距离估计RMSE为401.9 m。在收敛率方面，PLE-EKF收敛率为86%，而PLE-UKF收敛率为93%。因此，PLE-UKF较PLE-EKF有更快的收敛速度、更高的收敛率与更好的宽容性。

4 结束语

本文针对水声脉冲信号被动定位问题，提出了使用MAF-PLE-UKF联合方法进行位置距离估计。该方法解决了在参数估计误差较大时，传统 TMA方法容易发散、收敛性能差等问题。经过数据仿真实验，相比于传统UKF方法，该方法提升了19%的收敛率，并有效降低距离估计误差。而且，UKF算法在收敛速度、收敛率和宽容性上也明显优于EKF算法。本文的处理方法能够有效提升水声脉冲信号的被动测距性能。利用PLE进行距离初值估计时，系统协方差矩阵R中σΔT参数的设定对算法初始距离估计影响较大，需要进一步的研究，以改善系统性能。