具有弱τ-CS性质的环和模的扩张 ①

李煜彦, 李 锐

(陇南师范高等专科学校数信学院,甘肃 陇南 742500)

0 引言及预备知识

本文中的环都是有单位元的结合环,模指酉右R-模,挠理论均指遗传挠理论.设R是环,τ=(T,F)表示遗传挠理论,称N是M的τ-基本子模,如果Nτ-dM且NeM.用NM,Nτ-dM,Nτ-eM分别表示N是M的子模,τ-稠密子模,τ-基本子模.设R是环,称S是环R的右基本扩张环,如果RReSR.用Dτ(M)表示由M的所有τ-稠密子模构成的集合.称M是CS模,如果对任意NM,存在M的直和因子K,使得NeK.称M是C11模,如果对任意NM,存在M的直和因子K,使得K是N在M中的补.称M是τ-CS模,如果对任意Nτ-dM,存在M的直和因子K,使得Nτ-eK.令Zτ(M)={(m∈M|ann(m)τ-eRR}={(m∈M)|∃Lτ-eRR,mL=0}.称Zτ(M)是M的τ-奇异子模.如果Zτ(M)=M(Zτ(M)=0),那么就称M是τ-奇异(非奇异)模.由文献[1]知,Zτ(M)满足如下等式:

Zτ(M)=Z(M)∩τ(M)=τ(Z(M))=Z(τ(M)).

引理1[2]设M是模,KLM,则K∈Dτ(M)当且仅当K∈Dτ(L)且L∈Dτ(M),即Kτ-dM当且仅当Kτ-dL且Lτ-dM.

引理2[2]设K,NM.则K是N在M中的τ-补当且仅当K是N在M中的补,且K∩N=0,K⊕N∈Dτ(M).

由引理2和文献[3],易得下面引理.

引理3以下对模M等价:

(1)对任意Nτ-dM,存在M的直和因子K,使得K是N在M中的τ-补;

(2)对任意Nτ-dM,存在M的直和因子K,使得K∩N=0，且K⊕Nτ-eM.

定义1称M是τ-C11模,如果M满足引理3中条件之一.

显然,τ-CS模是τ-C11模.

1 本文主要结论

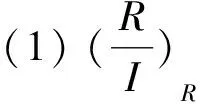
证明只证明(1),(2)的证明跟(1)是类似的.

“如果能够尽量在一天内把所有的检查完成，患者不用跑来跑去，付出的成本更少；宣教也可以集中，宣教服务人员时间一长也会越来越专业。”黄东胜院长指出。

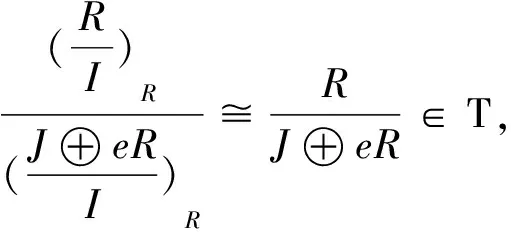
定理2设M是右R-模,L是M的全不变τ-稠密子模.若M是τ-C11模,则

(1)L是τ-C11模;

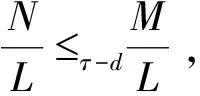
下面讨论τ-C11模以及右τ-C11环关于基本扩张的遗传性质.

定理3设R是环,S是R的右基本扩张环.若R是右τ-C11环,则以下结论成立:

(1)SR是τ-C11模;

(2)S是右τ-C11环.

证明只证明(1),(2)的证明跟(1)是类似的.

设XRτ-dSR,令Y=X∩R,则YR,且故Yτ-dR.从而存在e2=e∈R,使得eR是Y在R中的τ-补.下证(eS)S是X在S中的τ-补.

先证X∩eS=0.因为RReSR,所以Y=X∩ReX.假设存在0≠x∈X∩eS,则存在r∈R,使得0≠xr∈X∩R=Y.而x=ex,故0≠xr=exr∈Y∩eR.这与eR是Y的τ-补相矛盾.

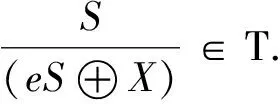
定理4设M是右R-模,Nτ-eM.设任意e∈EndR(N)都可以扩张到e′∈EndR(M),其中e=e2,e′=(e′)2.若N是τ-C11模,则M是τ-C11模.

证明设Lτ-dM.令D=N∩L,则即Dτ-dN.于是存在e2=e∈End(N),使得eN是D在N中的τ-补.由假设知,存在e′=(e′)2∈End(M),使得e′|N=e.易证e′M是L在M中的τ-补子模.从而M是τ-C11模.

2 结 语