时滞节能减排系统的复杂动力学特性分析 ①

司凤山, 徐 勇 , 王 晶, 王 娟

(1.安徽财经大学管理科学与工程学院，安徽 蚌埠 233030；2.北京跟踪与通信技术研究所，北京 100094)

0 引 言

随着经济的快速发展，巨大的能源消耗和污染物的排放，给人类生存环境和能源的可持续利用带来了严峻的挑战。于是采取何种措施有效协调能源价格及利用、碳排放、经济发展之间的关系是已成为目前亟待解决的一个重要课题。学者针对上述问题已经进行了相关研究，例如吕堂红等[1-2]通过研究能源价格模型，提出能源稳定性的定价策略和利用策略。田立新等[3-4]和殷红燕等[5]分析带时滞的能源价格模型，给出能源价格调整的稳定区间。Fang等[6]探究节能减排、碳排放、经济增长之间复杂的非线性博弈关系。本文基于以上研究，考虑经济增长对节能减排和碳排放影响的延迟效应，提出一个带时滞的节能减排模型，从系统稳定性和复杂性的角度给出延迟决策变量的稳定性区间，以增强节能减排系统决策的科学性。

1 时滞节能减排系统构建

文献[6]研究了如下的三维节能减排系统：

(1)

其中，x(t)是节能减排量，y(t)是碳排放量，z(t)是经济增长量(GDP)。a1为节能减排的发展系数，a2为碳排放对节能减排的影响系数，a3为GDP增长对节能减排的影响系数；b1为节能减排对碳排放的影响系数，b2为碳排放的发展系数，b3为GDP增长对碳排放的影响系数；c1为节能减排对GDP增长的影响系数，c2为碳排放对GDP增长的影响系数，c3为对节能减排的经济投入对经济增长的影响系数；ai,bi,ci>0,i=1,2,3。M,C,E,N>0，表示阈值。

因为节能减排和碳排放受到经济发展水平的影响，所以在制定下一期节能减排和碳排放策略时，不但要参照本期的经济增长量，而且还要参考历史的经济增长量，只有综合考虑才能制定出科学的策略。但是由于本期的经济增长量难以及时准确获取，故本文仅考虑参照历史的经济增长量来制定节能减排和碳排放策略。基于此，在系统(1)的基础上构建出带时滞的节能减排系统为：

(2)

其中，τ>0为时滞参数，它表示参照τ时刻之前的经济增长量来决策未来的节能减排和碳排放量。

2 系统稳定性分析

经计算得到系统(2)的有效均衡点为E(x*,y*,z*)，其中，

系统(2)在均衡点E处线性化为：

(3)

进而求得系统(3)在均衡点E处的特征方程为：

λ3+A2λ2+(A1+B1)λ+A0+B0+

(C1λ+C0+D0)e-λτ=0

(4)

其中，

B1=-a2b1，B0=-a2b1c3，

令λ=iω(ω>0)为式(4)的一个根，将其带入得到：

(5)

依据式(5)可以得到：

(6)

其中，

K1=A2C1-C0-D0,K2=A1C0+B1C0+A1D0+

B1D0-A0C1+B0C1,K3=C1,

K4=A2C0-A1C1-B1C1+A2D0,

由式(6)得到关于ω的方程为：

M4ω8+M3ω6+M2ω4+M1ω2+M0=0

(7)

其中，

假设条件(1)：式(7)至少有一个正实根ω0成立，则式(7)有一对纯虚根±iω0。此时根据式(6)得到时滞参数为：

(8)

特征方程(4)两边求λ关于τ的导数得到：

(9)

取式(9)的实数部分可得：

(10)

其中，PR和PI分别是式(10)分母的实部和虚部，QR和QI分别是其分子的实部和虚部，

即为：

PR=ω0C0sin(ω0τ0)+ω0D0sin(ω0τ0)-

QI=2A2ω0-C1sin(ω0τ0)。

结论1：对于系统(2)及其均衡点E，如果条件(1)-(2)都成立，则当τ<τ0时系统(2)在均衡点处局部渐近稳定；当τ>τ0时系统在均衡点处不稳定；当τ=τ0时系统在均衡点处产生Hopf分岔。

3 数值仿真

为了验证理论分析的正确性，以及更好地展现系统的复杂特性，故取其中的一组参数值为：a1=4.5,a2=1.3,a3=20,b1=0.25,b2=0.85,b3=0.35,c1=0.5,c2=0.3,c3=0.2,M=10,C=1,E=8,N=12，此时系统(2)的均衡点为E(-0.6323, 1.1440,-0.0516)。

3.1 τ对系统稳定性的影响

依据式(8)计算得到τ0=0.4622，根据结论1可知0.4622是系统(2)关于时滞参数产生Hopf分岔的临界值。系统(2)关于时滞参数τ的分岔图和最大李雅普诺夫指数图如图1所示。

(a)τ=0.44 (b)τ=0.48

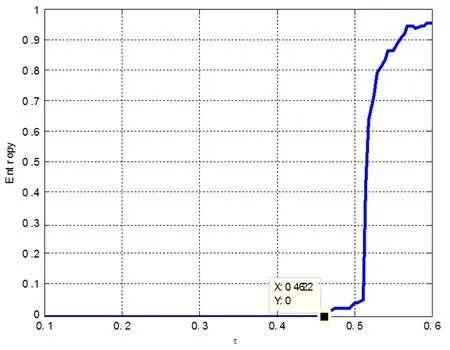
图3 系统(2)的熵图

图1(a)描述了系统由稳定状态通过分岔逐步进入混沌状态的过程，显然系统在τ=0.4622时产生分岔。由此可见，时滞参数过大会造成系统失稳，即政府在节能减排决策时参照的历史经济增长量不可过早。此外，最大李雅普诺夫指数(the Largest Lyapunov Exponent，缩写为LLE)是描述系统混沌特征的一个重要量化指标，指数小于零说明系统处于均衡态；当指数大于零说明系统处于混沌状态，其值越大意味着系统混沌越显著。从图1(b)可以看出，在τ=0.4622时指数等于零，此时系统处于稳定与不稳定之间的临界状态，这与图1(a)含义相同。同时说明，τ<0.4622是系统关于时滞参数τ的稳定域，而τ>0.4622是系统关于时滞参数τ的混沌域，这与结论1相一致。

为了直观展现分岔临界值左右两侧的系统状态，分别令τ=0.44<τ0和τ=0.48>τ0，此时对应的系统吸引子如图2所示。

由图2可知，当τ=0.44时系统(2)是稳定的，经长期博弈后将收敛于均衡点E。当τ=0.48时系统最后趋于极限环，呈现出不稳定状态。要避免这种失稳现象，必须缩短经济增长量对节能减排和碳排放影响的滞后时间。

3.2 τ对系统复杂性的影响

系统会受到各种因素的干扰而失去稳定。虽然系统可以通过自身调节或者外部干预使其由不稳定状态恢复至稳定状态，但是所用时长取决于系统的复杂程度。系统越复杂，其重返稳定状态的时间越长。熵(Entropy)是一个衡量系统复杂程度的指标，熵值越大意味着系统越复杂，反之亦然[9,10]。图3描述了系统熵值随τ增加的变化趋势，图中标注的点(0.4622,0)表示τ增加至0.4622时系统中的不稳定因素开始导致系统的复杂性发生变化，呈现出逐渐增加的态势。由此可见，图3中系统复杂性的变化趋势与图1中系统稳定性的变化趋势相同。

4 结 语

本文在节能减排系统中引入时滞参数，分析了时滞系统在均衡点处的Hopf分岔的存在性及条件，借助数值仿真讨论了时滞参数对系统稳定性和复杂性的影响，给出了系统的稳定域。研究表明，经济增长量对节能减排和碳排放的延迟效应存在时间范围限制，否则容易导致系统经分岔而陷入混沌状；且系统稳定性与系统复杂性具有相同的临界值，它们的变化趋势基本一致。只是探讨了带时滞的节能减排系统的动力学特性，没有对失稳系统进行稳定性控制，这将是下一步需要解决的问题。