关于广义斐波那契数列的线性空间结构的研究 ①
张小凤, 佟欣妍
(厦门工学院计算机与人工智能学院数学系,福建 厦门 361021)
0 引 言
生活中,会经常看到斐波那契数列的身影——松果、凤梨、树叶的排列,某些花朵的花瓣数…自然界并不懂得斐波那契数列,它们只是按照大自然的规律进化成这样。斐波那契数列作为大自然进化的“优化方式”,对它的研究自然意义重大,它是目前国际数学研究的一个前沿热点问题,吸引了众多数学家的研究兴趣,比如文献[1-5]。目前关于斐波那契数列的研究,大部分局限在数列自身的性质上。并且,数列本身也具有较大的局限,要求数列的前面两项是固定项。本文独辟蹊径,创新性地应用线性空间的理论来研究全体广义斐波那契数列,深入剖析它的数学涵义,刻画它的重要性质,得到了非常优美而富有意义的结论。这套全新的研究理论,在数学上拓展了斐波那契数列的深度和广度,同时让大家对于它的研究有了新的方向。
1 广义斐波那契数列的线性空间结构
1.1 广义斐波那契数列空间
定义1:一个数列{an}n≥1称为广义斐波那契数列,如果对于任意的i≥2,都有ai+1=ai+ai-1成立。所有广义斐波那契数列全体构成的集合记为。
定义2:对于任意两个数列{an}n≥1,{bn}n≥1以及任意实数λ,可以定义线性运算如下:
(1)加法运算:
{an}n≥1+{bn}n≥1={an+bn}n≥1;
(2)数乘运算:λ·{an}n≥1={λan}n≥1.
有下述结论:
定理1:在线性运算下,构成一个-线性空间。
证明:首先,对于∀F1={an}n≥1,F2={bn}n≥1∈,由F1+F2={an+bn}n≥1,有
ai+1+bi+1=(ai+ai-1)+(bi+bi-1)=(ai+bi)+(ai-1+bi-1),即F1+F2∈。
其次,对于∀λ∈,∀F={an}n≥1∈,由λF={λan}n≥1知,λai+1=λ(ai+ai-1)=λai+λai-1,即λF∈。
(1)加法交换律:∀F1={an}n≥1,F2={bn}n≥1∈,有F1+F2={an+bn}n≥1={bn+an}n≥1=F2+F1.
(2)加法结合律:∀F1,F2,F3∈,其中
F1={an}n≥1,F2={bn}n≥1,F3={cn}n≥1,
有
(F1+F2)+F3={an+bn}n≥1+{cn}n≥1=
{an+bn+cn}n≥1={an}n≥1+{bn+cn}n≥1=
F1+(F2+F3).
(3)零元:∃Ο={0}n≥1∈,使得对于任意的F={an}n≥1∈,
F+Ο={an}n≥1+{0}n≥1={an+0}n≥1={an}n≥1=F.
(4)负元:对于任意的F={an}n≥1∈,存在-F={-an}n≥1∈,使得F+(-F)={an+(-an)}n≥1={0}n≥1=Ο.对
(5)单位元1:∀F={an}n≥1∈,1·F=1·{an}n≥1={an}n≥1=F.
(6)数乘结合律: ∀λ,μ∈,F={an}n≥1∈,有
λ·(μ·F)=λ·(μ·{an}n≥1)=λ·{μan}n≥1=
{λμan}n≥1=λμ·{an}n≥1=(λμ)·F.
(7)数乘对加法的分配律:对于∀λ∈,∀F1={an}n≥1,F2={bn}n≥1∈,有
λ·(F1+F2)=λ·({an}n≥1+{bn}n≥1)=
λ·{an+bn}n≥1={λ(an+bn)}n≥1=
{λan+λbn}n≥1={λan}n≥1+{λbn}n≥1=
λ·F1+λ·F2.
(8)数量加法对数乘的分配律:对于∀λ,μ∈,∀F={an}n≥1∈,有
(λ+μ)·F=(λ+μ)·{an}n≥1=
{(λ+μ)an}n≥1={λan+μan}n≥1=
{λan}n≥1+{μan}n≥1=λ·{an}n≥1+
μ·{an}n≥1=λ·F+μ·F.
1.2 广义斐波那契数列空间的基与维数
定理2:对于-线性空间,{F(0,1),F(1,0)}构成它的一组基。
证明:设k1F(0,1)+k2F(1,0)=0,则k1F(0,1)+k2F(1,0)=F(k1,k2)=0,从而k1=k2=0,即F(0,1)与F(1,0)线性无关.
另外,对于∀F(a,b)∈,有F(a,b)=aF(1,0)+bF(0,1),
故F(0,1),F(1,0)构成F的一组基。 证明完毕.
推论1:-线性空间的维数为2, 即dim=2。
2 广义斐波那契数列的通项公式
广义斐波那契数列F(0,1),F(1,0),F(1,1)的通项公式已经有人陆续给出,下面给出前两项可以是任意实数的广义斐波那契数列F(a,b)的通项公式。
定理3:对于任意a,b,记F(a,b)={fn}n≥1,则F(a,b)的通项公式为:
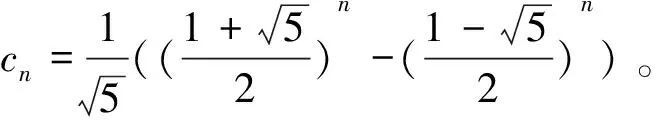
根据定理2,知道F(a,b)=a·F(1,0)+b·F(0,1),从而F(a,b)的通项公式为:
fn=a·an+b·bn=a·cn-2+b·cn-1=
定理证明完毕.
本文首次从线性代数的角度来研究广义斐波那契数列空间,证明它具有线性空间结构,并给出它的基与维数的刻画。另外,突破了传统的对于斐波那契数列的研究前两项必须是固定项这一重要局限,给出了前两项可以是任意项的广义斐波那契数列的通项公式。因此,本文的研究方法和所得结论,都具有重要的意义。

