基于GA-BP神经网络的自建点PM2.5浓度校准研究 ①

尤 游， 王 蒙

(安徽机电职业技术学院1.公共基础教学部;2.互联网与通信学院，安徽 芜湖 241000)

0 引 言

随着社会经济的发展和居住环境的改善，空气质量问题越来越受到人们的关注。及时做好空气质量的精确预测对环境管理、污染控制都有重要的参考意义[1]。空气质量主要通过空气质量指数(AQI)的大小来衡量，影响指标包括六种污染物(PM2.5、PM10、CO、NO2、SO2、O3)的日常监测浓度。数据以国家控制站点(国控点)监测数据为准，但由于国控点的布控较少，发布时间滞后，无法给出实时监测和预报，所以大多城市监测到的数据为自建点数据，由于监测设备以及环境因素的影响，自建点数据与国控点数据存在一定的差异，所以需要借助国控点数据对自建点数据进行校准，减少预报误差[2]。

这里PM2.5指的是空气中动力学当量直径小于等于2.5μm的颗粒物[3],是影响空气质量的重要因素，所以文中以PM2.5为例进行校准，其他污染物同理。自建点PM2.5浓度产生偏差有很多原因，包括污染物以及环境因素，而这些指标间存在着较复杂的非线性映射关系，所以引入BP神经网络来构建校准模型，由于BP算法存在一定的缺陷，如权值和阈值的随机性等，进一步利用遗传算法优化BP神经网络，构建GA-BP神经网络校准模型，并通过测试样本的校准误差来比较两种模型的优劣性。

1 变量的选取和分析

研究以2019年“高教社杯”全国大学生数学建模竞赛D题为参考对象，原始数据来源于该题附件[2]。首先对数据进行预处理和时间匹配，得到自建点6种污染物浓度、5个环境影响因素(风速、压强、降水量、温度、湿度)浓度以及对应的国控点PM2.5浓度。神经网络模型中，以自建点PM2.5浓度、其他5种污染物(PM10、CO、NO2、SO2、O3)浓度以及5个环境影响指标为输入变量，国控点PM2.5浓度为输出变量组成训练样本，训练结束后再对测试样本进行预测，获得自建点PM2.5浓度校准值，即为输出层。

模型校准效果通过平均绝对百分比误差(MAPE)和均方误差(MSE)来衡量，公式如下：

(1)

(2)

这里xi和yi分别指国控点PM2.5浓度和自建点PM2.5浓度的校准值，N为测试样本数。

2 相关理论介绍

2.1 BP神经网络

BP算法的基本学习过程包括信号的正向传播与误差的反向传播两个阶段。它由输入层、隐含层和输出层构成。训练样本在正向传播过程中，从输入层经过隐含层再到输出层，如果输出结果达不到期望输出，则转入反向传播阶段，根据设置的预测误差不断调整各神经元的权值和阈值，反复循环，直到满足期望输出[4]。设计的BP神经网络结构如图1所示。在构建神经网络之前需要确定各层的节点数，这里输入、输出层节点数由原始训练样本决定，而隐含层节点数一直都未有确定的算法，一般通过试错法来确定，即通过不断的调试降低预测误差来确定最优节点数。常用的隐含层节点数经验公式如下：

(3)

其中，l为隐含层节点数，μ,ν分别表示输入、输出层神经元节点数，ω取0-10中的任意整数。

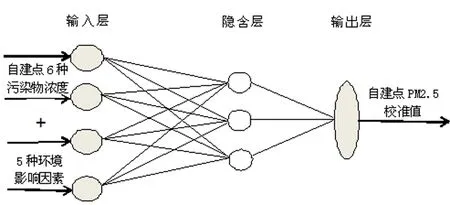
图1 自建点PM2.5浓度校准BP神经网络结构

设X为输入变量矩阵，W、V分别为输入层到隐含层、隐含层到输出层的权值矩阵，∂、β分别为隐含层和输出层的阈值矩阵，这样得到隐含层的输入变量为XW+α，输出变量为P=f(XW+α)，同理输出层的输入变量为PV+β，输出变量即最终输出为

Y=g(PV+β)=g(f(XW+α)V+β)

(4)

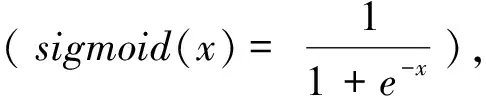
2.2 遗传算法优化BP神经网络(GA-BP神经网络)

遗传算法(Genetic Algorithm，简称GA)是由美国J.Holland教授于1975年提出来的一种优化算法，是通过模拟生物界适者生存进化规律而演化出来的。算法的核心是将问题的可行解通过染色体编码随机生成初始种群，通过适应度函数计算个体适应度值，按照适者生存的原则保留能适应环境的个体，淘汰其余个体，然后通过遗传操作(选择、交叉、变异)得到子代种群，反复迭代最终进化得到最适应环境的个体[5,6]。

BP神经网络运用范围广，能较好的模拟出非线性映射关系，但在训练过程中其梯度下降算法由于权阈值的随机性，易出现局部最优、迭代时间过长、过渡拟合等问题，而遗传算法利用群体搜索技术，通过解码操作能得到最优的权值和阈值，所以利用遗传算法优化BP神经网络，可以克服以上弊端，具体步骤如下[5,6]：

(1)建立初始BP神经网络。确定隐含层节点数，学习率，预测误差等参数；

(2)初始化种群。个体的染色体编码长度为：long=μ·l+l·v+l+v，这里μ、l、ν分别表示输入层、隐含层和输出层的神经元节点数。

(3)GA函数和适应度函数设计。GA函数通过调用GAOT工具箱，适应度函数以自建点PM2.5浓度校准值与国控点PM2.5浓度的误差函数的倒数为准。

(4)遗传操作循环。通过选择、变异、交叉等遗传操作确定新的子代种群，计算个体适应度，如果达到循环条件(满足进化代数)，则遗传算法结束，否则循环继续。最终将适应度最大的个体通过解码操作输出为最优权值和阈值。

(5)GA-BP神经网络训练。将得到的最优权阈值赋给BP神经网络，对样本重新进行仿真预测。

3 算例仿真

样本数据中，将通过分层抽样得到的80个样本作为神经网络的训练样本，剩下随机抽样的30个样本组成测试样本。这里，神经网络输入层节点数为11维，若直接输入可能会导致收敛速度过慢，且变量数目较多不能排除多重共线性，所以在构建神经网络之前，先对输入变量进行PCA降维处理，即先进行主成分分析。

主成分分析通过计算相关矩阵的顺序特征值和对应的特征向量，得到自变量的主成分相互独立，克服了多重共线性，然后根据累积贡献率选择保留原始信息。通过MATLAB运行得到前四个主成分的累积贡献率为97.67%，所以选择前四个主成分作为输入样本，测试样本同理。设前四个主成分依次为F1,F2,F3,F4，得到

F1=0.0951x1+0.1848x2+0.0008x3+0.0653x4+

0.0164x5+0.0837x6+0.0006x7+0.9627x8+

0.1121x9+0.0105x10+0.0764x11

(5)

F2=0.4332x1+0.8649x2+0.0010x3+0.0346x4+

0.0113x5+0.0767x6-0.0012x7-0.2278x8+

0.0648x9-0.0073x10+0.0292x11

(6)

F3=0.0320x1-0.1053x2+0.0025x3+0.0504x4+

0.0054x5+0.9044x6-0.0003x7-0.0478x8+

0.1080x9+0.0690x10-0.3856x11

(7)

F4=-0.0998x1-0.0572x2-0.0011x3+0.5811x4+

0.0382x5+0.2736x6-0.0118x7-0.1081x8+

0.0660x9-0.1067x10+0.7384x11

(8)

图2 国控点与BP输出值的曲线比较图

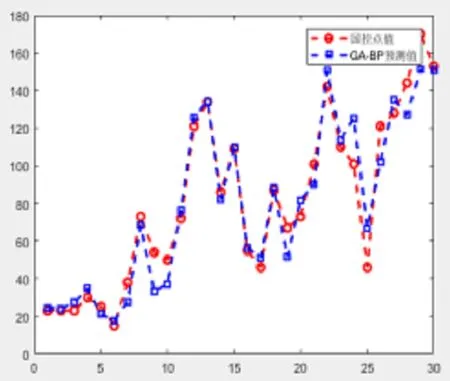
图3 国控点与GA-BP输出值的曲线比较图

接下来利用新的主成分向量作为训练样本，并对其进行归一化处理，此时最小误差设为0.0001，学习率为0.01，迭代次数为1000，隐含层神经元个数由公式(3)得到选取范围为[3,10]，根据试错法原则确定最佳隐层神经元个数为6，于是建立4-6-1结构的BP神经网络模型，再对测试样本进行预测，通过反归一化最后得到自建点PM2.5浓度校准值。

为了衡量模型效果，将校准值与国控点PM2.5浓度对比，分别得到其平均绝对百分比误差为21.87%，均方误差为0.0599。观察具体数据发现部分自建点校准效果较差，说明BP神经网络模型有待改进。

下面利用遗传算法优化BP神经网络，构建GA-BP神经网络模型，这里染色体长度为S=4×6+6×1+6+1=37，种群规模设为50，遗传代数为100次，变异概率为0.09，交叉概率为0.95，通过调用GAOT工具箱，同理得到GA-BP神经网络的平均绝对百分比误差为12.56%，大大降低了预测误差，均方误差为0.0197，也优于BP神经网络，说明GA-BP神经网络模型的校准效果更好。具体对照见表1。另外从图2、图3全部测试样本的的国控点(期望输出)与神经网络实际输出数据对比，也能得出GA-BP神经网络拟合效果更优的结论。

表1 模型校准效果对照表

4 结 语

通过分析自建点PM2.5浓度与其影响因素之间存在非线性映射关系，所以选用BP神经网络对自建点数据进行校准。但单一的BP神经网络算法容易陷入局部最优、收敛速度慢和过拟合的困境[7]，所以引用遗传算法来优化BP神经网络，通过遗传操作确定最优的权值和阈值，构建GA-BP神经网络模型，通过案例仿真能看出GA-BP神经网络校准效果符合预期，同时对其他污染物浓度的校准也具有借鉴价值。模型可以明显提高空气质量预报的准确度，推动环境监测工作的进展，具有一定的应用前景。