合成信息系统与有限个子系统的属性特征研究 ①

方连花， 林玉梅， 李克典

(1.泉州信息工程学院2.通识教育中心，福建 泉州 362000,3.闽南师范大学数统学院,福建 漳州 363000)

0 引 言

粗糙集理论[1]是继概率论、模糊集、证据理论之后的又一个刻画不完整性和不确定性的数学工具。目前，许多学者从各个方面对目标信息系统的知识获取和规则提取做了深入的研究，并且取得了大量成果[2-8]。一个信息系统的知识库往往都是确定的，但在实际应用中，经常会在原信息系统上添加有限个研究对象，或者增加(删除)属性特征，进而对新信息系统进行分类、知识获取等等。在这方面，已经有学者对其进行了研究，文献[9]在等价关系的前提下研究了合成信息系统与子信息系统的属性约简问题。由于现实中有些信息是不确定、不完备或者是多值的系统，文献[10]在优势关系下研究序信息系统的合成与分解的属性特征，文献[11]和[12]分别在拟序关系下研究合成集值信息系统以及决策表的属性特征。他们的研究主要是基于两个信息系统的合成，而在实际问题中并不仅仅只有两个子系统的合成与分解，信息系统中又会存在大量的冗余数据，因此研究有限多个信息系统的合成以及其属性特征是有必要的。给出任意有限个对象合成信息系统和有限个属性合成信息系统的概念，分别讨论了它们的属性特征与有限个原子信息系统的属性特征之间的关系。

1 对象合成信息系统

定义1.1[5]I=(U,A,F)是一个信息系统，其中

U是对象集，U={x1,x2,…,xn}；A是条件属性集，A={a1,a2,…,ap}；

F是U与A的关系集，F={fk:U→Vk,k≤p}，Vk是ak的有限值域。

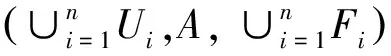
信息系统中的不同属性对划分有不同的作用，有的属性是必不可少的，称为核心属性；有的属性是可以被其他属性代替的，称为相对必要属性；有的属性是根本不需要的，称为不必要属性。下面给出这三种属性特征的数学刻画。

定义1.3[13]设I=(U,A,F)是一个信息系统，对于B⊆A，若RB=RA,称B是划分协调集。若B是划分协调集，而B的任何真子集均不是划分协调集，则称B是划分约简集。

定义1.4[13]设I=(U,A,F)是一个信息系统，Bk(k≤r)为所有划分约简集，

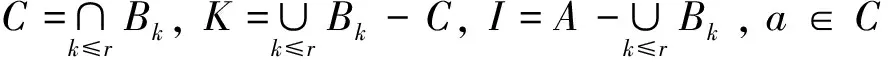
在信息系统中，为了研究不同属性的特征，在文献[14]和[15]中有如下等价刻画定理：

定理1.1[14]设(U,A,F)是信息系统，则有以下结论：

(1)a是划分核心当且仅当RA-{a}≠RA；

(2)a是划分不必要属性当且仅当R(a)⊆Ra，其中R(a)=∪{RB-{a}|RB⊆RA,B⊆A}；

(3)a是划分相对必要属性当且仅当RA-{a}=RA成立且R(a)⊆Ra不成立。

定理1.2[15]设(U,A,F)是信息系统，则有以下结论：

(1)a是划分核心当且仅当RA-{a}⊆Ra不成立。

(2)a是划分不必要属性或者划分相对必要属性当且仅当RA-{a}⊆Ra成立。

根据定义1.3、定义1.4和定理1.1、定理1.2可以得到对象合成信息系统的协调集、不必要属性、相对必要属性与n个原子信息系统的属性特征之间的关系。

定理1.3设(∪Ui,A,∪Fi)为信息系统(U1,A,F1)，(U2,A,F2)，…，(Un,A,Fn)的对象合成信息系统，B⊆A。若B是(∪Ui,A,∪Fi)的一个约简，则B分别是(U1,A,F1)，(U2,A,F2)，…，(Un,A,Fn)的协调集。

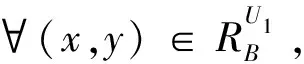
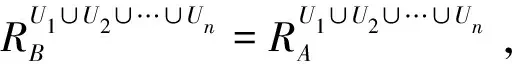
同理可证，B分别是(U2,A,F2)，…，(Un,A,Fn)的协调集。

定理1.4设(∪Ui,A,∪Fi)为信息系统(U1,A,F1)，(U2,A,F2)，…，(Un,A,Fn)的对象合成信息系统，a∈A。若a是(∪Ui,A,∪Fi)的不必要属性，则a分别是(U1,A,F1)，(U2,A,F2)，…，(Un,A,Fn)的不必要属性。

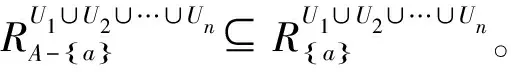
同理可证，a分别是(U2,A,F2)，……，(Un,A,Fn)的不必要属性。

定理1.5设(∪Ui,A,∪Fi)为信息系统(U1,A,F1)，(U2,A,F2)，…，(Un,A,Fn)的对象合成信息系统，则(U1,A,F1)，(U2,A,F2)，…，(Un,A,Fn)的核心属性一定是(∪Ui,A,∪Fi)的核心属性。

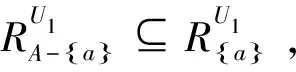
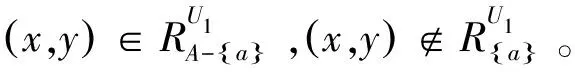
同理可证，(U2,A,F2)，…，(Un,A,Fn)的核心属性是(∪Ui,A,∪Fi)的核心属性。

例1.1通过例子验证定理1.3、定理1.4和定理1.5的结论。

设(U1,A,F1),(U2,A,F2),(U3,A,F3)是三个信息系统，表1是它们的对象合成信息系统(U1∪U2∪U3,A,F1∪F2∪F3)，其中A={a,b,c}，U1={x1,x2,x3}，U2={x4,x5,x6,x7}，

U3={x8,x9,x10,x11,x12}。

由划分的定义可得对象合成信息系统(U1∪U2∪U3,A,F1∪F2∪F3)的等价类为{x1,x9,x11}，{x2,x3,x8}，{x4,x6}，{x5,x7,x10}，{x12}。

根据辨识矩阵，容易得出{a,c}是(U1∪U2∪U3,A,F1∪F2∪F3)的一个约简，则由定理1.3知，{a,c}分别是(U1,A,F1),(U2,A,F2)和(U3,A,F3)的协调集；容易验证{b}是(U1∪U2∪U3,A,F1∪F2∪F3)的不必要属性，则由定理1.4知，{b}分别是(U1,A,F1),(U2,A,F2)和(U3,A,F3)的不必要属性；容易验证{c}是(U1,A,F1)的核心属性，由定理1.5知{c}是(U1,A,F1),(U2,A,F2),(U3,A,F3)的核心属性。

2 属性合成信息系统

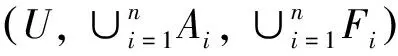
Ai∩Aj=∅,i≠j。

定 理2.1设(U,∪Ai,∪Fi)为系统(U,A1,F1)，(U,A2,F2)，…，(U,An,Fn)的属性合成系统，对于任意的Bi⊆Ai，若Bi是(U,Ai,Fi)的一个约简，则∪Bi是(U,∪Ai,∪Fi)的协调集。

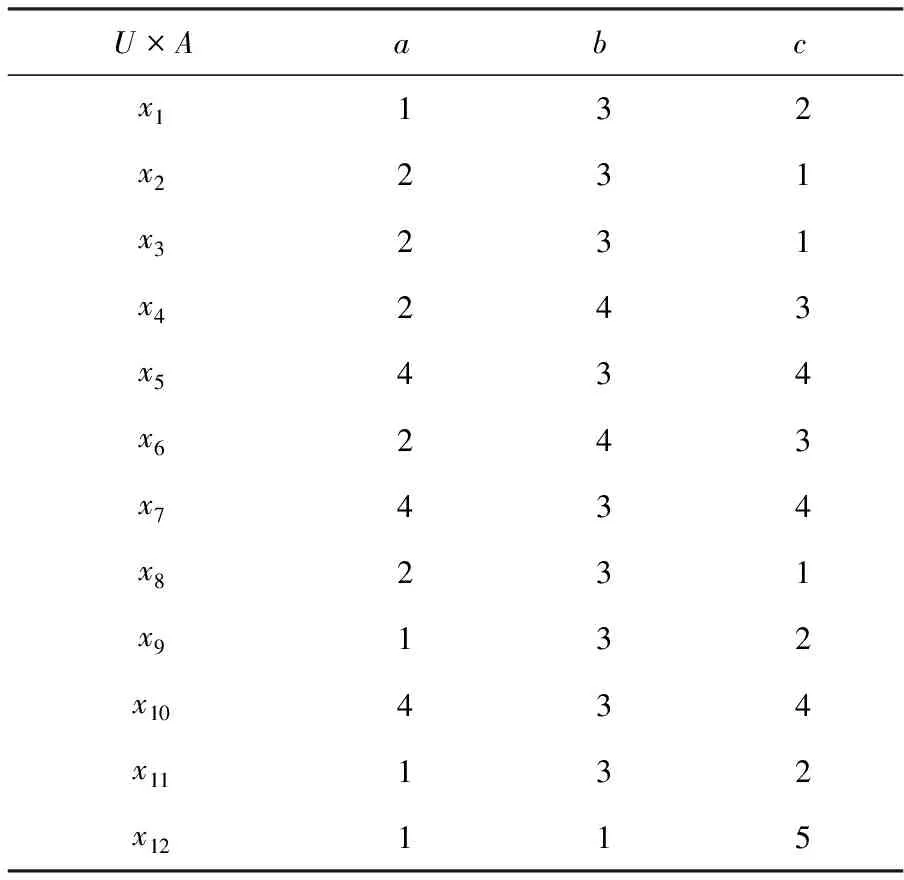
表1 对象合成信息系统

证 明：设∀(x,y)∈RB1∪B2∪…∪Bn，若RB1∪B2∪…∪Bn=∩RBi则(x,y)∈∩RBi。若∩RBi=∩RAi=RA1∪A2∪…∪An则(x,y)∈RA1∪A2∪…∪An，即RB1∪B2∪…∪Bn⊆RA1∪A2∪…∪An。另一方面，RA1∪A2∪…∪An⊆RB1∪B2∪…∪Bn。因此，RA1∪A2∪…∪An=RB1∪B2∪…∪Bn，即∪Bi是(U,∪Ai,∪Fi)的协调集。

定理2.2设(U,∪Ai,∪Fi)为信息系统(U,A1,F1)，(U,A2,F2)，…，(U,An,Fn)的属性合成信息系统，则(U,A1,F1)，(U,A2,F2)，…，(U,An,Fn)的不必要属性一定是(U,∪Ai,∪Fi)的不必要属性。

证 明：设a∈A1是(U,A1,F1)的不必要属性，则由定理1.2可知RA1-{a}⊆R{a}。若RA1∪A2∪…∪An-{a}⊆RA1-{a}，则RA1∪A2∪…∪An-{a}⊆R{a}，所以a是(U,∪Ai,∪Fi)的不必要属性。

同理，(U,A2,F2)，…，(U,An,Fn)的不必要属性一定是(U,∪Ai,∪Fi)的不必要属性。

定理2.3设(U,∪Ai,∪Fi)为信息系统(U,A1,F1)，(U,A2,F2)，…，(U,An,Fn)的属性合成信息系统，a∈∪Ai。若a是(U,∪Ai,∪Fi)的核心属性，则当a∈Ai时，a是(U,Ai,Fi)的核心属性。

证 明：设a∈Ai是(U,∪Ai,∪Fi)的核心属性，则由定理1.2可知RA1∪A2∪…∪An-{a}⊆R{a}，即∃x,y∈U，满足(x,y)∈RA1∪A2∪…∪An-{a},(x,y)∉R{a}。又因为RA1∪A2∪…∪An-{a}⊆RAi-{a}，故(x,y)∈RAi-{a}，即RAi-{a}⊆R{a}。因此，a是(U,Ai,Fi)的核心属性。

3 结 语

目前关于知识系统合成的研究都是基于两个信息系统的合成，而在实际问题中并不仅仅只有两个子系统的合成与分解，信息系统中又会存在大量的冗余数据，因此研究有限多个信息系统的合成以及其属性特征是有必要的。文中给出了任意有限个对象合成信息系统和有限个属性合成信息系统的概念，分别讨论了它们的核心属性、不必要属性、相对必要属性等属性特征与有限个原子信息系统的属性特征之间的关系。并通过实例验证了该方法的有效性，为今后进一步研究合成信息系统与有限个子信息系统的属性约简问题奠定了基础。