叶片振动放大夹具振动特性数值分析

朱大巍，祝济之，王新，刘春华

（航天瑞莱科技有限公司，苏州 215129）

引言

叶片是航空发动机的重要部件，疲劳破坏是导致航空发动机叶片出现裂纹及断裂的主要原因之一。航空发动机叶片疲劳试验是发动机改进设计和故障分析的必要环节。航空发动机涡轮叶片的振动疲劳试验一般采用共振方法[1]，采用正弦定频信号激励叶片，频率为叶片共振频率，获得较高的振动响应。此方法要求叶片刚性固持在激励设备上，用榫头或榫齿的安装方式尽量模仿叶片在发动机工作状态时的受力形式。尽管在叶片的共振频率附近，但是某些叶片仍然要求较高的基础激励量级，才能达到设计的应力水平。

解决叶片激励量级不足一般有两种方法：①用附加质量块的方式降低叶片的固有频率，以此来增加激励振幅[2]。“附加质量块”的方式可以使试验顺利的进行，但是叶片应力分布会受到影响。②采用具有振动放大效应的夹具，提高叶片承受的基础激励。具有振动放大特性的夹具已经应用到实际的叶片试验中，姚春斌等[3]采用模态分析方法设计了叶片频率上具有放大效应的夹具并应用到振动疲劳试验中，该夹具通过变动约束位置的方法调整夹具的振动放大频率范围。所设计的放大夹具使用具有较大的工程意义，但是对夹具放大的振动特性分析较少。另外，采用约束位置变动调整夹具频率，在实施过程中具有较多的不确定因素和不可控因素，导致叶片调试困难较多。

为了获得夹具振动放大的一般特性，指导叶片振动放大夹具设计。本文先将叶片和夹具组合进行力学简化，采用梁模型来模拟叶片及夹具[4]。根据该模型获得夹具的振动放大特性，并在此基础上进行参数分析，讨论个参数对夹具振动放大能力的影响。

1 叶片及夹具简化振动模型

1.1 几何结构

叶片疲劳试验示意图如图1所示，大多数叶片的疲劳试验是在振动台上完成的。试验时，叶片装在夹具上，然后夹具固定在振动台台面上，振动台的运动部件带动夹具与叶片一起振动。振动台输出固定频率（一般为叶片1阶弯曲固有频率）的正弦信号，激励叶片进行同频率的正弦强迫振动。

1.2 振动简化模型

振动台对夹具施加的激励方向垂直于夹具和叶片，夹具及叶片横向为垂直于激励方向，因此可以用梁理论来分析叶片和夹具的振动特性[4]。基于上述假设，可得到叶片疲劳试验的简化模型，如图2所示，采用梁模拟叶片与夹具，叶片和夹具的连接部件假设为刚性连接，采用集中质量模拟连接部件的质量效应。

2 振动特性分析

2.1 结构参数

根据图2的简化模型建立叶片疲劳试验的有限元模型，应用ANSYS APDL进行计算分析[5]。模拟叶片梁结构及模拟夹具的结构尺寸及材料参数见表1和表2。叶片的1阶弯曲频率为2 308.3 Hz，重量为17.67 g，夹具的重量为2.24 kg。通过修改夹具的弹性模量调整夹具频率。

2.2 模态分析

叶片夹具组合前2阶频率随夹具1阶频率变化曲线如图3所示，夹具1阶频率远离叶片1阶频率时，叶片夹具组合前2阶频率分别接近夹具和叶片的1阶频率；当夹具1阶频率接近叶片1阶频率时，夹具和叶片发生耦合，叶片夹具组合前2阶频率偏移夹具和叶片的1阶频率。

根据模态和振动理论可知，在叶片1阶频率附近，叶片振动形态和1阶频率类似。因此可用叶尖与叶根的相对位移表征叶片的振动量级。提取叶片夹具组合前2阶振型的叶尖位移幅值和叶根位移幅值，计算叶尖/叶根的传递曲线，如图4所示。夹具1阶频率低于叶片1阶频率时，叶片夹具组合1阶频率为夹具振动主导；当夹具1阶频率高于叶片1阶频率时，叶片夹具组合1阶频率为叶片振动主导。当夹具和叶片的1阶频率重合时，叶片夹具组合的1阶和2阶频率下叶片的振动放大系数是相同的。

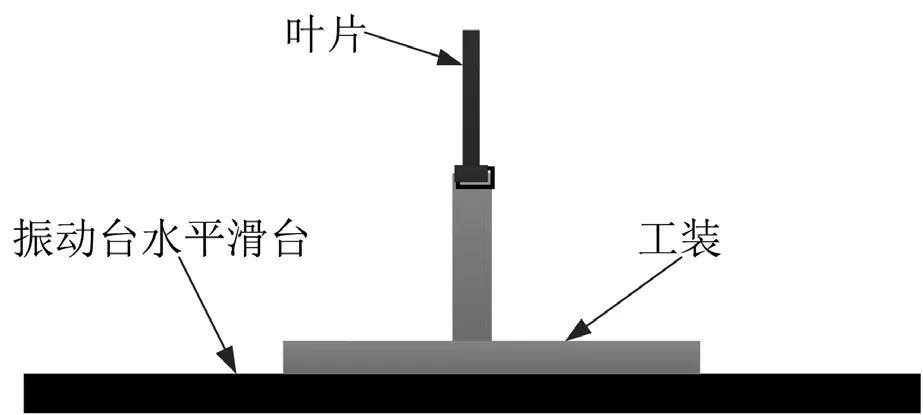
图1 振动台叶片测试结构

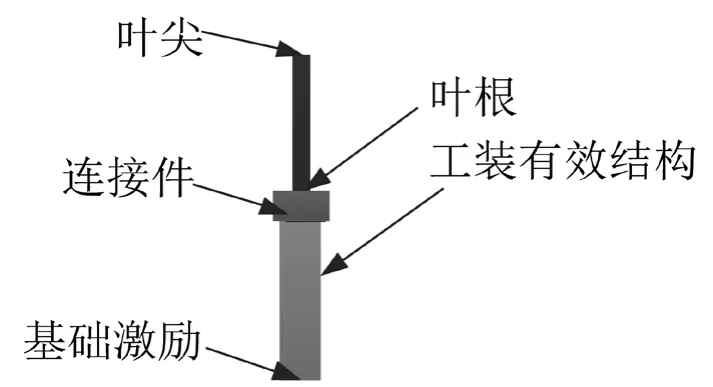
图2 叶片简化梁模型

表1 叶片及夹具模拟梁尺寸

表2 叶片材料参数

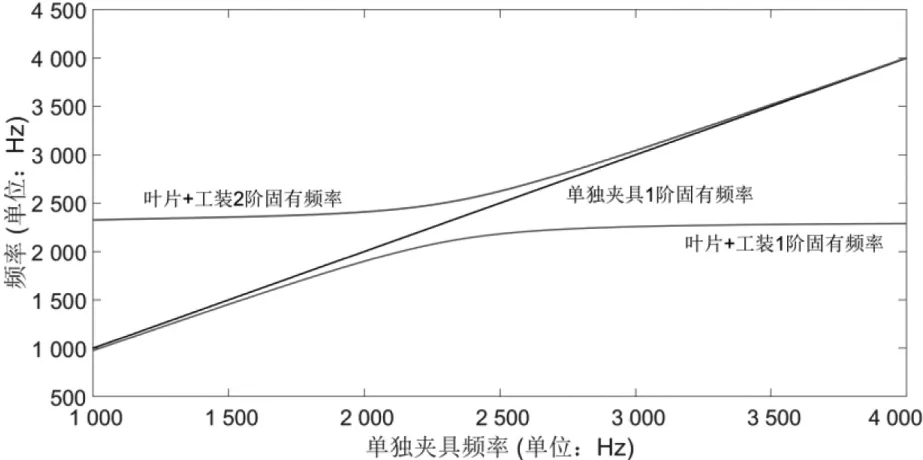
图3 叶片夹具组合频率随夹具频率变化

2.3 谐响应分析

叶片疲劳试验采用定频正弦信号进行基础激励，使叶片产生预定的位移。令夹具和叶片的1阶频率保持一致，在夹具基础上施加1e-4m的基础位移激励，阻尼为0.01，分析夹具的传递特性。图5是叶根及叶尖相对于激励位置的位移传递率，图6是叶尖相对于叶根的传递率。由图可见，在固有频率处，叶片根部的振动放大率为峰值。需要注意的是，虽然叶片夹具组合的固有频率为位移响应峰值点，但是对于叶片，自身的1阶共振频率点为叶尖相对叶根振动传递率的峰值。装在夹具上的叶片，叶片相对叶尖的传递要高于刚性体夹具的传递率。计算结果表明：①叶片根部的振动量级明显高于输入的激励量级；②叶片的共振峰值仍然在叶片的1阶频率处，但是该频率下夹具的振动放大率较小；③装在夹具上的叶片1阶频率处的振动放大率高于刚性夹具上的叶片放大率。

2.4 结论

从叶片夹具的分析结果可知，采用共振放大原理的夹具可以提高叶片根部的振动量级，并提高叶片的振动传递率。叶片疲劳试验主要是采用应力（或应变）和叶尖幅值之间的关系来标定叶片的振动量级，所以叶片的激励频率只与循环次数相关，试验时的频率可以为叶片及夹具的共振频率，叶片的应力（或应变）与叶片的相对位移正相关，可以用叶尖和叶根的位移传递率表征夹具的振动放大能力。

3 参数分析

3.1 夹具1阶频率

当夹具1阶频率和叶片频率接近时，夹具明显的具有振动放大特性。将夹具1阶频率作为变量，分析叶片夹具组合第1和第2阶固有频率点的振动特性，如图7所示。可见，在夹具1阶频率等于叶片1阶频率时，叶尖的位移最大。图8为夹具的传递曲线，以叶片1阶频率为分界，夹具1阶频率小于叶片频率时，叶片夹具组合的1阶频率（夹具为主导振动）夹具振动放大较大明显；夹具1阶频率大于叶片频率时，叶片夹具组合的2阶频率（夹具为主导振动）夹具振动放大较大明显；夹具1阶频率等于叶片频率时，叶片夹具组合两阶固有频率点上，振动放大率相等；夹具1阶频率与叶片1阶频率越接近，夹具振动放大相对稍小。

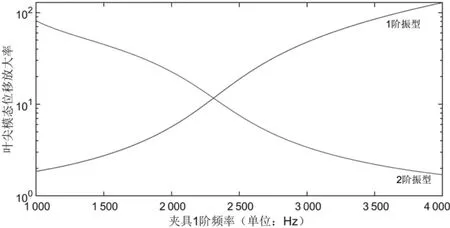
图4 叶尖相对叶根模态位移放大率

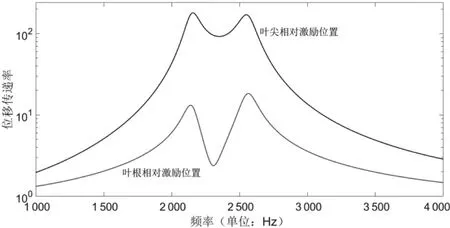
图5 叶根及叶尖相对于激励位置的传递率

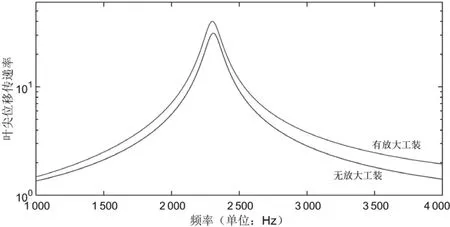
图6 叶尖相对于叶根的传递率

图7 不同夹具与叶片组合固有频率点叶尖对应激励位置位移传递率

为了考察叶片的振动量级，以叶尖与叶根的相对位移传递率为参数代表叶片的振动量级。图9为叶尖相对位移的振动传递率曲线，叶片夹具组合前两阶固有频率点对应振动放大的峰值；在叶片1阶频率附近，叶片夹具组合第1阶固有频率点振动放大率大于第2阶固有频率点的振动放大率。

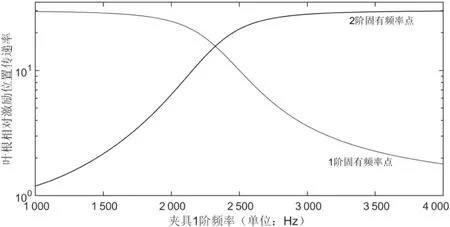
图8 不同夹具与叶片组合固有频率点叶根对应激励位置位移传递率

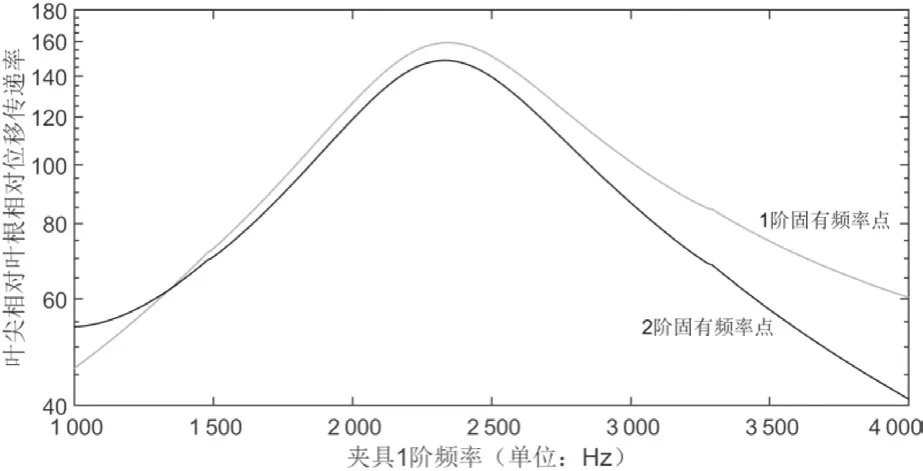
图9 不同夹具与叶片组合固有频率点叶尖对应叶根位移传递率

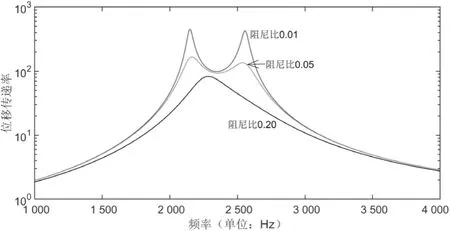
图10 叶尖相对激励位置传递率

3.2 阻尼

将夹具阻尼作为调整参数，其它参数保持不变。图10和图11分别是叶尖和叶根相对激励位置的传递率曲线，由图可见，阻尼增大时，夹具的振动放大率出现较大的衰减，叶尖传递率峰值向叶片自身的固有频率点靠近，从双峰变成单峰。夹具的阻尼特性对叶片的振动影响较小。

3.3 附加质量变化

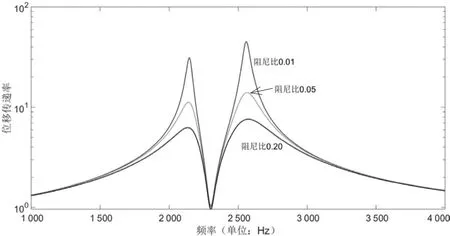
图11 叶根相对激励位置传递率

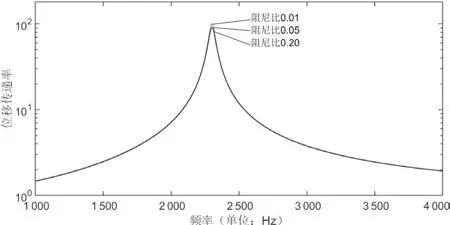
图12 叶尖相对叶根位移传递率

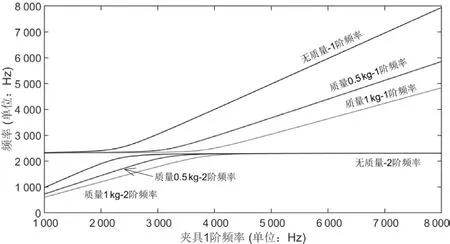
图13无质量、质量为0.5 kg和质量为1 kg时叶片和夹具组合的固有频率

叶片需要用固定装置装到夹具上，固定装置具有一定的质量。图13是无附加质量、附加质量0.5 kg和附加质量1 kg时叶片夹具组合前两阶固有频率曲线，由图可见，附加质量逐渐加大时，叶片和夹具组合的固有频率下降，为了与叶片1阶频率保持一致，需要更高的夹具刚度。

图15和图16为无附加质量、附加质量0.5 kg和附加质量1 kg时激励频率为1阶和2阶固有频率时叶尖相对位移的振动位移传递率。由图可见，当附加质量增大时，叶片夹具组合的固有频率上叶片相对位移振动传递率上升。

4 结论

本文建立了叶片夹具组合的梁模型，分析了夹具的振动特性。分析结果表明：

1）采用共振放大机理设计的夹具可以有效的提高叶片根部承受的激励量级，叶根处的振动量级远大于激励量级。当夹具1阶频率和叶片1阶频率吻合时，虽然夹具的振动放大效果相对较小，但是叶片的振动量级最大。

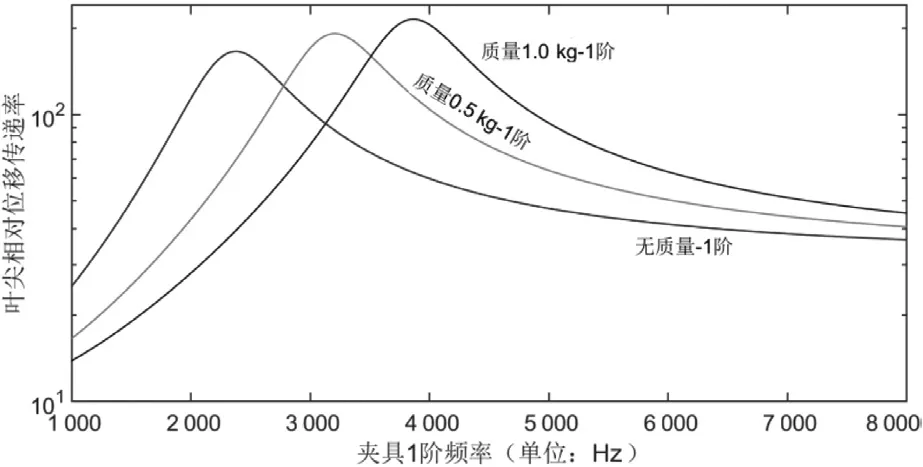
图14 无质量、质量为0.5 kg和质量为1 kg时叶尖相对位移传递率

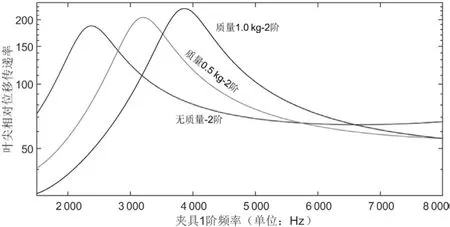
图15 无质量、质量为0.5 kg和质量为1 kg时叶尖相对位移传递率

2）叶片夹具组合的1阶频率点和2阶频率点比叶片自身的1阶频率具有更高的激励效率，而叶片夹具组合的1阶频率比2阶频率具有较高的激励效率。

3）在叶片根部增加附加质量可以提高夹具的振动放大能力，并且可以改变夹具和附加质量组合的固有频率，可以用于夹具组合系统的频率调整，使夹具1阶频率与叶片1阶频率高度吻合。