航空发动机叶片声振模态试验方法研究
陈国一,雷霆,王和,刘军,李丽远
(1.天津航天瑞莱科技有限公司,天津 30000;2.北京强度环境研究所,北京 100076)
引言
叶片作为航空发动机关键部件,其工作环境复杂恶劣,经受复杂载荷环境,极易发生损坏[1],并且发动机的叶片经常进行高周疲劳试验,而叶片的模态分析可以为高周疲劳试验提供数据支撑,有效开展后续高周振动疲劳试验[2]。也可通过模态分析和有限元结算结果相比较,验证有限元计算的准确性。但叶片自身的质量较轻,采用接触式传感器对试验结果可能会存在附加质量影响。目前国内外均利用激光等非接触测量技术解决这种问题,但是这种试验方法中的成本较高,试验的过程也比较复杂。本文通过取某发动机某级动叶叶片进行模态测试分析,采用声压传感器进行模态试验,与传统接触式测量方法进行比对,通过前三阶次的固有频率、振型、阻尼对比分析,最终确定针对叶片模态试验的最适用方法。
1 基本理论
叶片模态试验中,一般利用加速度传感器进行模态试验,采用力锤进行激励,获取加速度传感器的响应信号,对激励信号和加速度信号的传递函数进行模态拟合得到频率、振型、阻尼比等参数,这种方式在模态试验中比较通用,但对于叶片的这种轻质量结构件来说未必适用。而基于声振的互易原理,采用声压传感器进行模态测试,基于振动和声的互易性,在参考点激励,测量响应点的声压量级,得到两者的频响函数,进行模态参数拟合[3,4]。
互易性原理:

第i点给予激励力,j点得到声压量级,得到的频响函数在第j点用声源进行激励,在i点得到响应,得到的频响函数大小相同,方向相反。
声振的方程为:

式中:
x—为结构位移;
p—声压;
Ks—结构刚度矩阵;
KcT——转制置矩阵;
Kf—流体刚度矩阵;
Kc—结构响应和声学激励;
Ms—流体质量矩阵;
Cs—结构阻尼矩阵;
Cf—流体阻尼矩阵;
ρ—介质密度;
f—结构激励;
q—体积速度。

且 As=(Kf-jωCf-ω2Mf)/ρ
则式(1)简写为

式(2)导出两个声振频响函数矩阵
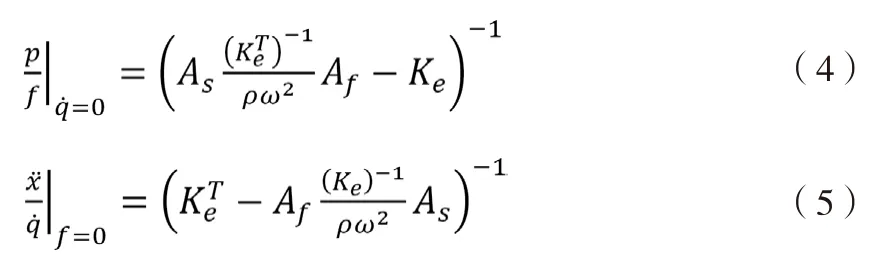
进行结构模态分析时,如叶片,环境是不封闭的,一点体积声源发出的功率W,其中能被板吸收用于产生振动的为固定的比例系数β。因此式(1)可为:

在发动机叶片模态试验中,为了获取较高的信噪比,应使传声器位置尽可能的靠近被测结构,以使β值尽可能大。且测试过程中一般不变动传声器,保证β值不变。
2 叶片模态试验方法
进行叶片模态试验方法须有一种前提假设,由于实际大多数叶片结构不是均匀厚度的,分为进气边和排气边,进气边厚度比较大,排气边相对较薄,并且整个叶身部位有很大曲率。因此试验结构采用近似的方法,会使最终分析得到的振型图与实际叶片振型有部分偏差。但这种偏差对于叶片的固有频率和阻尼基本没有影响。
2.1 使用加速度测点方法
本例中采用粘贴加速度传感器方法进行叶片模态试验,在叶片上放置1个加速度传感器和30个测点(如图1、图2),分析频率为1 500 Hz。把叶片、夹具刚性连接,测点24#位置的背面粘贴加速度传感器,采用锤击法进行试验。利用MIMO(多输入多输出)计算每个测点的响应与参考信号的频响函数,使用ERA算法进行拟合,得出叶片前三阶的固有频率、振型和阻尼比。
2.2 使用声振法进行模态试验
同尺寸同规格的叶片,采用声振法进行模态试验,也采用MIMO(多输入多输出)得到模态参数。在叶身部位布置3个声传感器和30个测点(如图1、图2),分析频率为1 500 Hz,其中测点7#、13#、24#为声传感器布置点。同样的安装固定方式,移动力锤进行模态测试。通过得到声压级计算每个测点的响应与参考的频响函数,最终得出叶片前三阶的固有频率、振型和阻尼比。

图1 叶片安装状态
3 试验结果分析与讨论
通过对力锤激励下,逐个测量叶片上每个点的响应,进行所有测点的频响函数计算(如图3),采用ERA模态拟合方式(如图4),最终可以得出叶片前三阶固有频率、振型和阻尼比等模态参数。

图2 叶片声振法模态试验测点分布
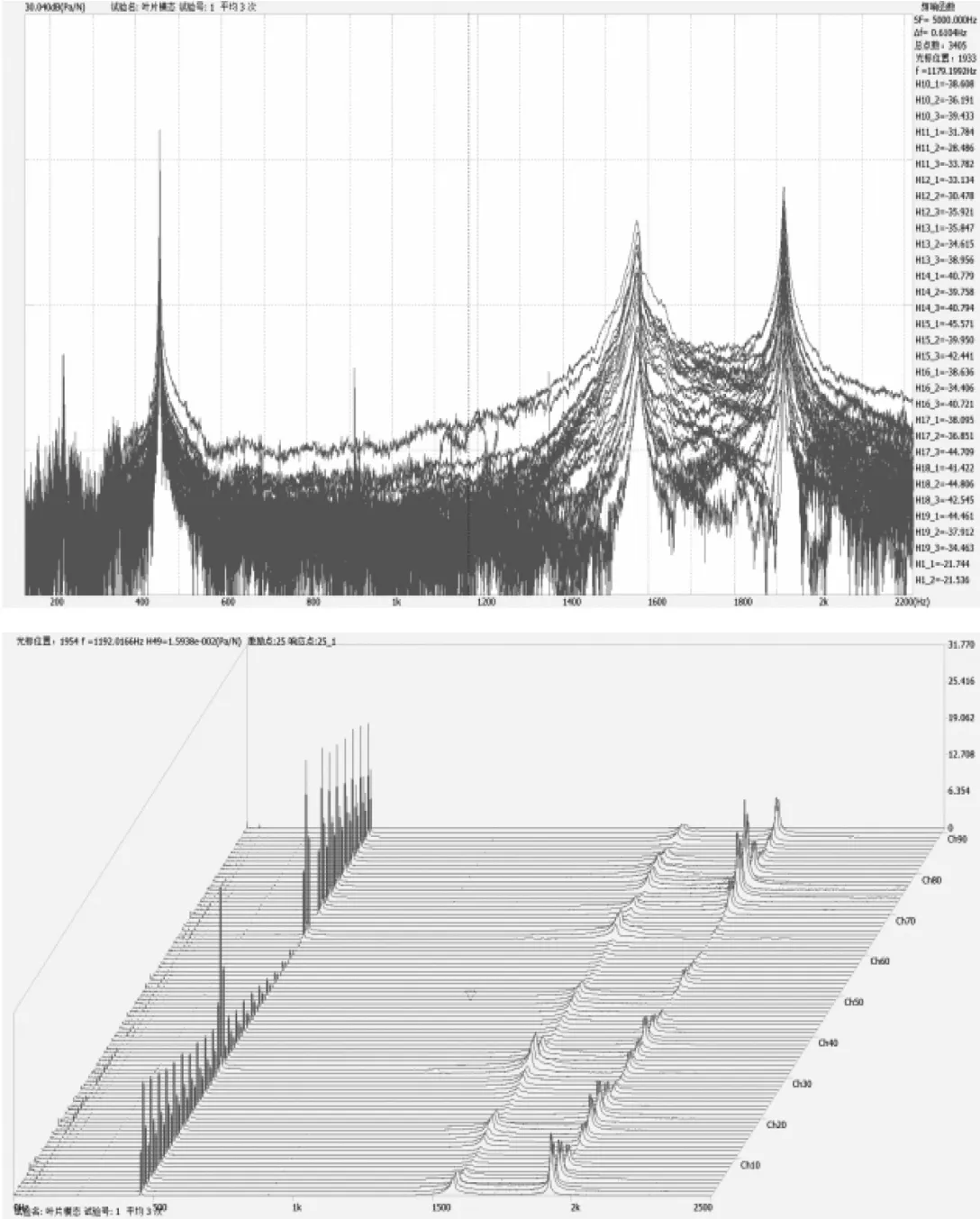
图3 叶片声振模态试验频响函数图

图4 叶片声振模态试验参数稳态图
叶片前三阶的声振法模态试验及加速度法模态试验结果见表1所示。
对比声振法模态试验和加速度法的模态参数结果可以发现:
1)声振法相对于加速度法的一阶没有更多的改变,这是由于粘贴加速度传感器位置选择相对较好,试验中通过不同位置粘贴的传感器数据差异性很大,这里不进行详细阐述。而变换声振传感器的位置对试验结果影响并不大,分析得出附加质量对模态参数影响较大。
2)声振法模态试验相比较加速度法,模态的结果改善明显。
3)声振法相对于加速度法更接近于计算结果,两者模态频率差异为3 %以内。
4 结论
本文主要研究航空发动机叶片的模态试验方法,并且主要研究一阶模态,因为通常在振动试验过程中,通常一阶模态参数为研究重点,从整个研究过程中可以得出:通过声振模态和加速度模态试验结果对比,利用声传感器代替加速度传感器的模态试验方法确实合理可行,声振模态试验方法也更适用于航空发动机叶片模态试验。并且对于附加质量影响比较严重的产品,利用声振模态也均能得到比较好的模态参数。

表1 叶片前三阶试验结果比对

图5 声振法模态振型

图6 加速度法模态振型

