基于混合威布尔分布的电能表寿命预测研究

滕永兴，曹国瑞 ，杨霖，钟睿君，朱逸群，李祺

（1.国网天津市电力公司电力科学研究院，天津 300384；2.天津大学电气自动化与信息工程学院，天津 300072）

为贯彻落实国家电网公司“集团化运作、集约化发展、精益化管理、标准化建设”的管理要求，加快两个转变、实现“一强三优”现代化工作的重要内容，2013年天津电力公司开始采用计量资产全寿命周期管理系统。目前，智能表大规模换装已完成，电能表已经实现采集目标全覆盖，随着电改、综合能源战略转型等环境变化，智能电能表故障发生的预测、供应商选择决策对于提高资产质量来说显得越来越重要。

国内对电能表评价以及寿命预测方面研究已经取得很多成果。文献[1]从全生命周期的角度评价电能表质量，将质量评价环节延伸到设计阶段，综合考虑了设计、生产、检测、运行、报废鉴定等环节，计算出各电能表厂家的电能表综合得分。文献[2]将智能电能表全寿命周期中不同阶段的故障率、合格率、专家评分等相关数据来构建评价体系，用k均值聚类分析方法给出电表性能等级的划分。文献[3]采用改进型定量战略计划矩阵对电能表影响因素进行定量归类，并引入灰色理论、模糊数学对电能表性能进行最终指标综合评判。文献[4]结合电子产品可靠性工程经验，分析智能电能表的整个生命周期过程所面临的环境条件，各阶段存在的可靠性问题，探讨了智能电能表可靠性评价的考虑要素。文献[5]利用高斯正态分布理论分析电能表误差分布概率的置信度，组合不同影响因素来评价电能表的计量准确性。文献[6]利用概率神经网络和决策树算法进行不良数据检测，并且与神经网络进行了对比分析。文献[7]结合威布尔分布的失效特性，基于智能电能表发生故障时间和通过计算出来的经验分布函数，利用最小二乘估计法，确定威布尔分布模型的尺度参数和形状参数，对电能表的特征量指标等寿命数据进行分析以确定其寿命分布，进而分析电能表的实际可靠性性能。

大多数研究是基于运行中电能表的信息，从可靠性的角度对电能表进行评估和寿命预测，而基于故障数据进行分析的研究很少[8-10]。本文基于天津电力公司智能电能表故障数据，使用故障树将多种故障归类，找出概率最高的3种故障，采用适用于电子器件的混合威布尔模型，利用大量真实数据估计参数，从而得到可靠度函数并预测电能表寿命。在此基础上，横向对比多家供应商产品可靠性，并为其提供产品改进指导。

1 模型理论

1.1 数据预处理

天津电力公司自2013年开始进行拆回电能表分拣处理的方法探索与技术研究，研发了国内首条拆回电能表自动分拣处理系统，实现电能表分拣集中处理和分拣工作全自动化，在确保拆回电能表数据质量的同时，最大限度地减少人工投入，达到提高效率和降低拆回电能表管理成本的目标。截止到2018年6月，天津电力公司依托自动分拣系统，已对拆回的21万只故障电能表构建故障信息库。通过筛选其中相对完整且查明故障类型的电能表信息，共得到108 391条来自33家不同供应商的电能表故障数据，包括09版电能表105 287条和13版电能表3 104条。根据电能表硬件结构特点，可将其视为由多个相互独立的元器件串联组成，本文使用故障树分析法对故障类型进行归类。选取“电能表失效”为顶事件，各元器件故障为中间事件，故障类型为底事件，建立电能表失效故障树，如图1所示，故障树各事件说明如表1所示。

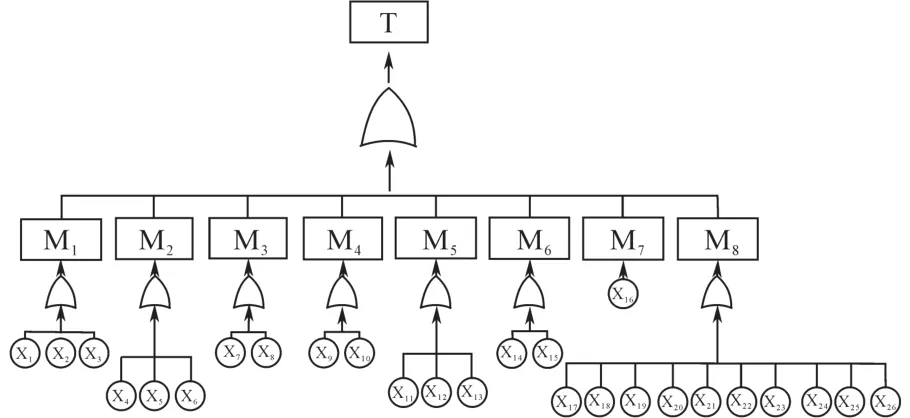
图1 电能表失效故障树Fig.1 Fault tree of watt-hour meter failure

表1 电能表失效故障树事件说明Tab.1 Fault tree event explanation of watt-hour meter failure

从图1中可以看出，电能表失效故障树主要包括8个或门，影响因素主要包括8个中间事件和26个底事件。从故障发生情况来看，由于电池故障、显示故障和电路故障发生频数占比最高，且远高于其他故障，可视为电能表失效的主要原因。因此，选取该三种元器件的故障数据进行电能表可靠性分析。

1.2 混合威布尔分布模型

对于设备可靠性研究来说，威布尔分布模型能够较为灵活地描述可靠性在整个寿命周期内的变化情况[11]。混合威布尔分布模型是由多个相互独立的单一威布尔分布模型[12]构成，能对较为复杂的情况进行拟合，比单一威布尔分布模型更加贴近实际情况[13]。将电能表看作由电池模块（M1）、显示模块（M2）和电路模块（M3）3个子体组成的总体，每个子体均服从单一威布尔分布，其失效分布函数为

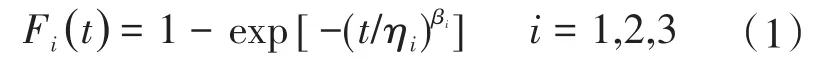
式中：t为电能表运行时间；i为子分部编号；βi为第i个子分部的形状参数；ηi为第i个子分部的尺度参数。

失效概率密度函数为

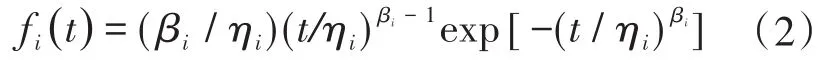
可靠度函数为

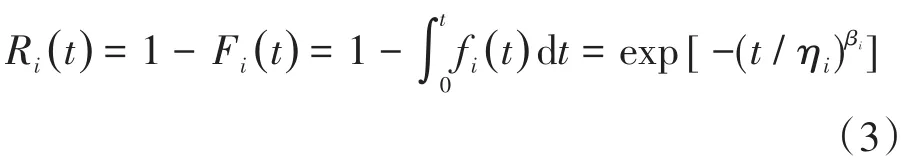
电能表的总体失效概率密度函数为

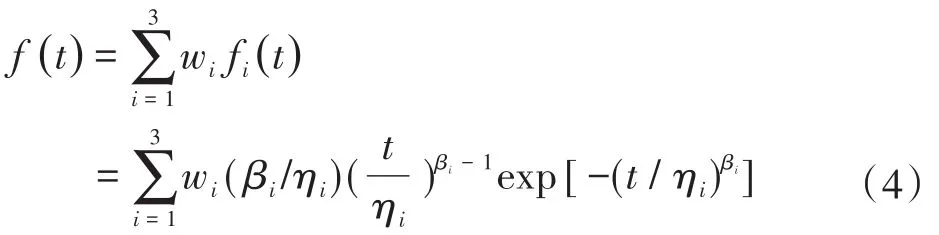
其中，wi为第i个子分部的权重系数，表示第i个元器件发生故障的频次在总故障频次中所占的比例，且满足。

混合威布尔分布模型的可靠度函数为

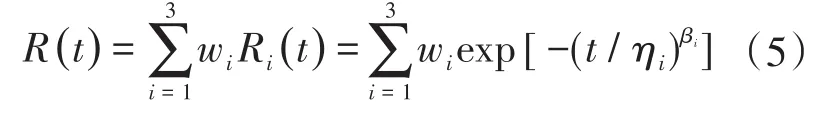
电能表的平均寿命为

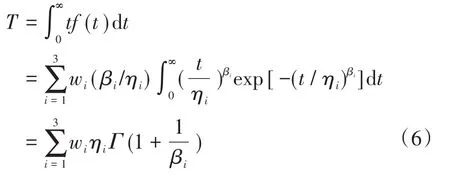
式中：Г为伽马函数[14]。

1.3 参数估计

利用最小二乘法对单一威布尔分布模型进行参数估计[15]。由威布尔失效分布函数取自然对数：

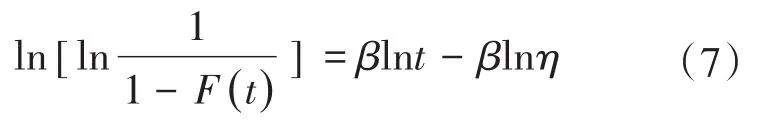
相应的单一威布尔参数表达式为

2 实例分析

2.1 09版电能表可靠性分析

经筛选，从故障数据库中得到105 287条09版电能表故障数据，其中M1有90 253条，M2有7 623条，M3有7 411条。将各模块故障数据按运行时间大小排序，失效分布函数与相关参数值如表2所示。

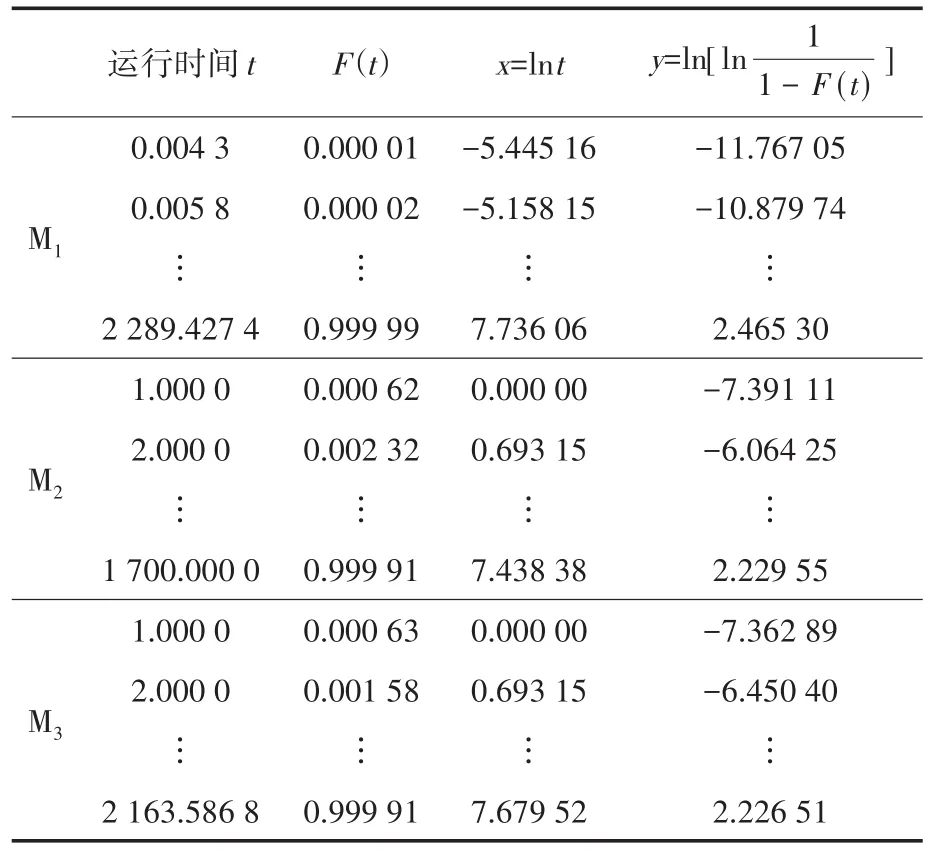
表2 09版电能表故障数据参数值Tab.2 Fault data parameter value of watt-hour meter version 09

将表2中各模块的x和y值代入回归系数最小二乘解表达式中，分别得到三项故障的混合威布尔参数β1=2.264，η1=1 246；β2=1.242，η2=723.7；β3=1.235，η3=634.9；根据各模块故障发生频次占比，得到子分布权重系数w1=0.857，w2=0.072，w3=0.070。

09版电能表的可靠度函数为

概率密度函数为

绘制可靠度R（t）曲线与实际故障数据对比情况如图2所示。

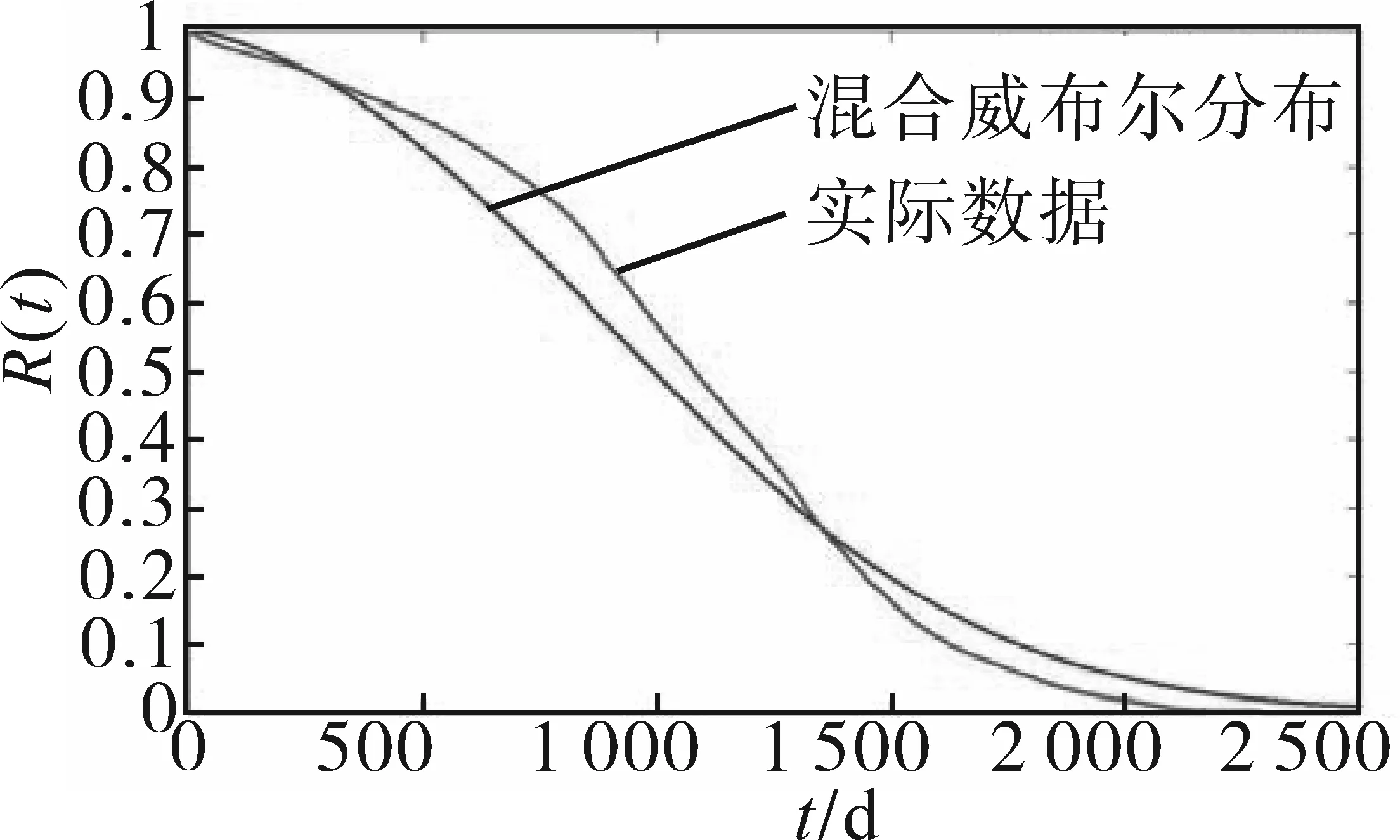
图2 09版电能表可靠度曲线Fig.2 Reliability curves of watt-hour meter version 09

由图2可以看出，混合威布尔分布模型对真实数据的拟合效果良好，该模型能有效地反映电能表的可靠度。结合图3中的概率密度f（t）曲线，可以看出，09版电能表在运行初期可靠性较好，在运行至1 000 d时进入故障高发期。经计算，09版电能表的平均寿命T=1 036 d。

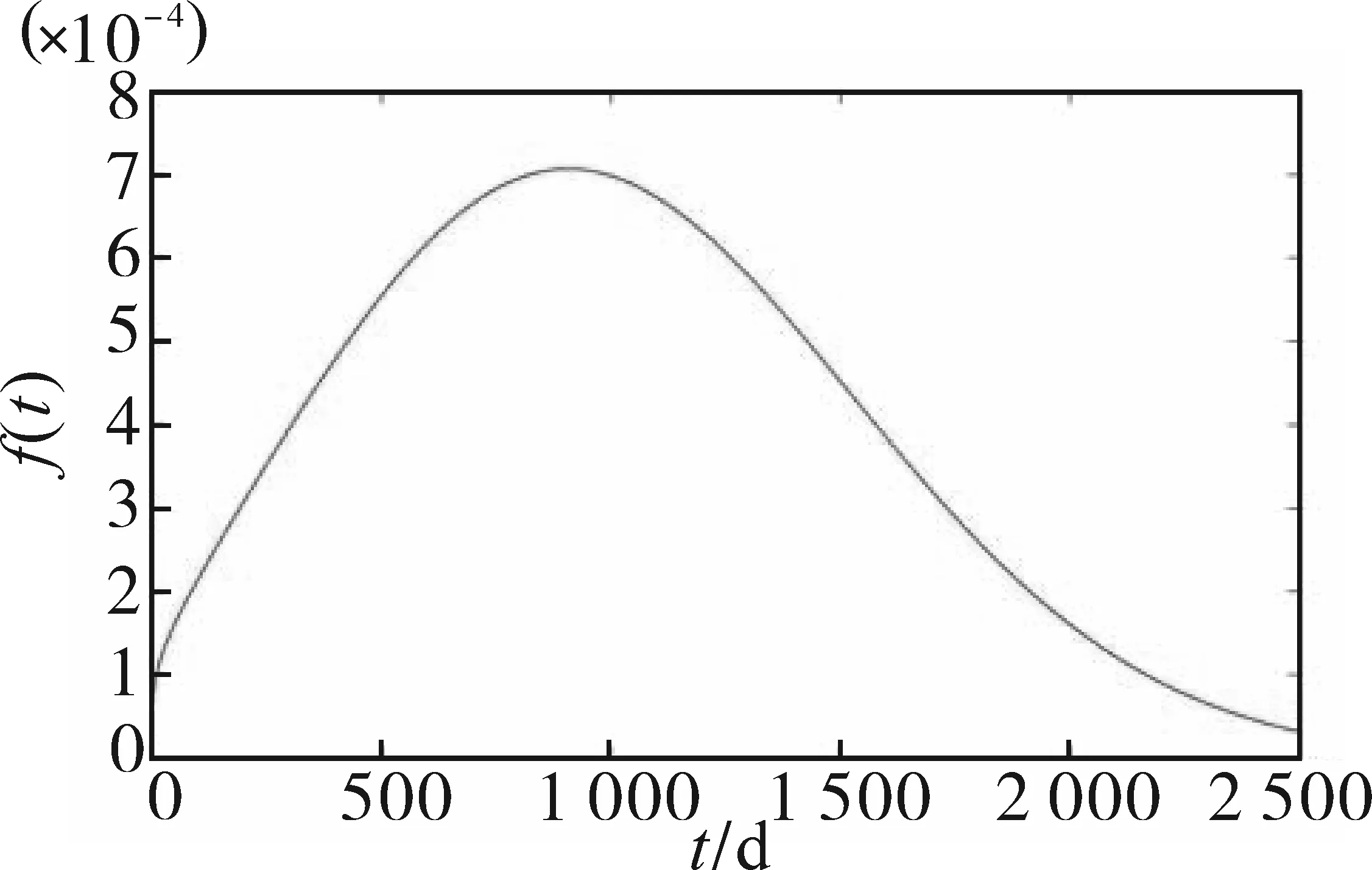
图3 09版电能表概率密度曲线Fig.3 Probability density curves of watt-hour meter version 09

对比09版电能表的3个重要模块性能，电池模块（M1）、显示模块（M2）和电路模块（M3）的概率密度曲线如图4所示。可以看出，显示模块（M2）和电路模块（M3）的性能较为相似，在电能表投入使用初期发生故障的概率较高，在运行200 d左右达到故障高峰，随后失效概率随运行时间增长而逐渐减小。而电池模块（M1）在电能表投入使用初期性能较好，随着运行时间增长，发生故障的概率逐渐增大，并在运行至1 000 d左右达到故障高峰。

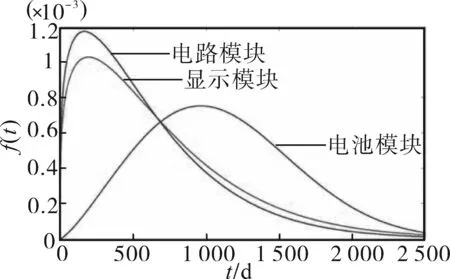
图4 09版电能表各模块概率密度曲线Fig.4 Probability density curves for the modules of watt-hour meter version 09

通过对比图3和图4可知，电能表整体性能的变化趋势主要由电池模块（M1）决定，从子分布权重系数也可以看出，电池故障是导致09版电能表失效的主要原因。为提高09版电能表的可靠性，延长使用寿命，应注重电池模块性能的优化。此外，显示模块（M2）故障和电路模块（M3）故障在一定程度上增加了电能表在运行初期发生故障的概率，为电能表运行初期的故障排查提供了参考。

2.2 多供应商电能表可靠性分析

选取电能表供应量较大的5家供应商，用同样方法分别得到混合威布尔参数，如表3所示，相应的可靠度曲线和概率密度曲线分别见图5和图6。

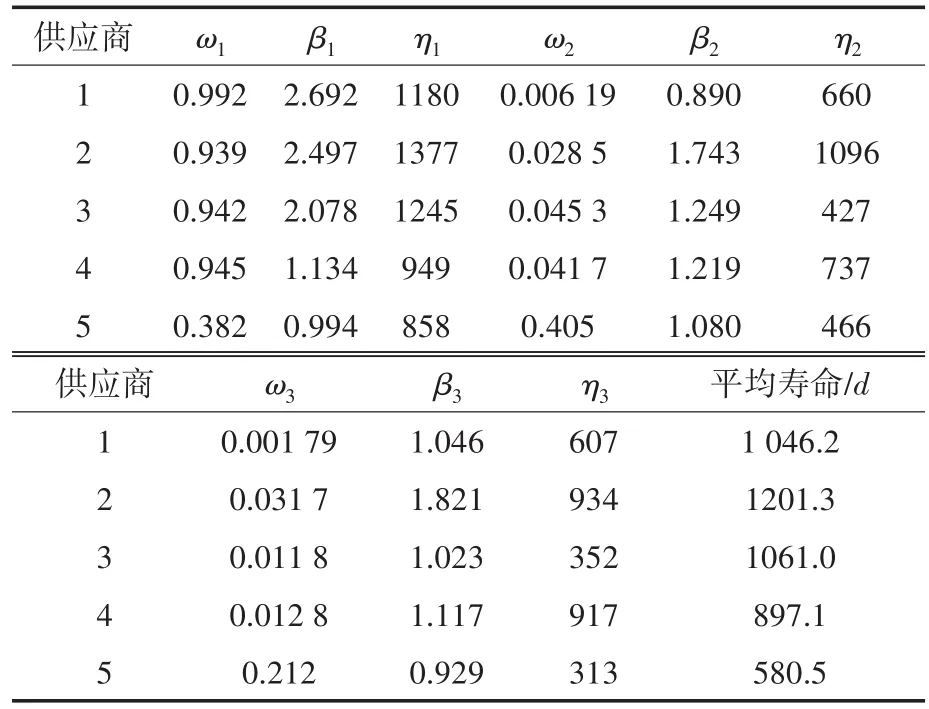
表3 5家供应商电能表混合威布尔参数Tab.3 Mixed Weibull parameters of five suppliers′watt-hour meters

图5 5家供应商电能表可靠度曲线Fig.5 Reliability curves of watt-hour meters from five suppliers

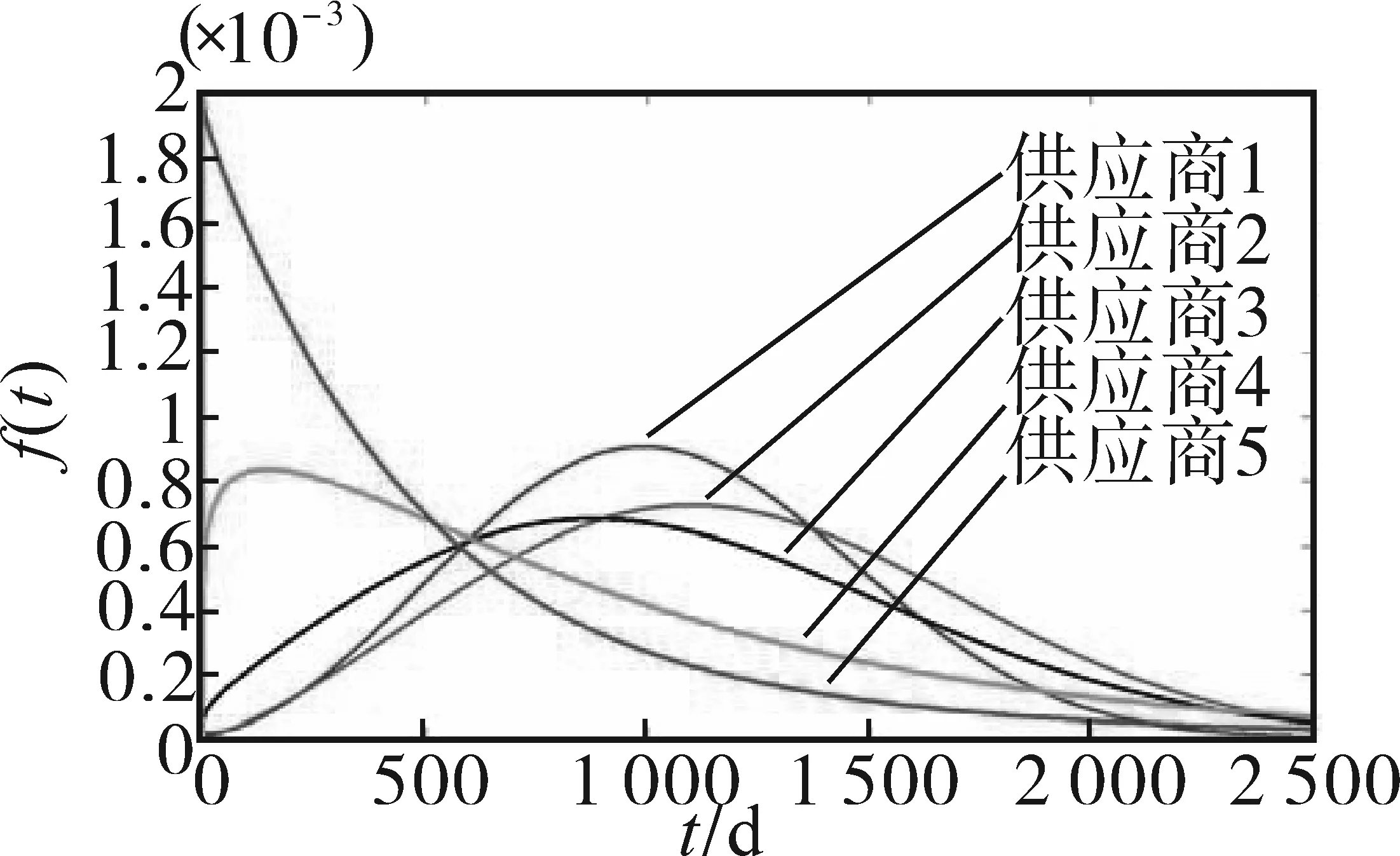
图6 5家供应商电能表概率密度曲线Fig.6 Probability density curves of electric energy meters from five suppliers

由图5和6可以直观地看出，供应商1～供应商3的电能表在使用初期的故障概率较低，然后随运行时间增加持续上升，在使用1 000 d左右达到故障高峰；供应商4和供应商5在电能表使用初期故障概率较高，之后持续降低，初期可靠度下降较快。供应商2的电能表故障高峰发生时间最晚，且峰值较低，因此可靠性最好；供应商5的电能表运行初期即达到故障高峰，且远高于其他4家供应商的故障峰值，因此可靠性最差。在运行初期，供应商1可靠性优于供应商3，但在运行后期情况相反，这是因为，该两家供应商的电能表性能变化趋势较为相近，供应商1的故障高峰发生时间晚于供应商3，但峰值相对略高。从计算出的平均寿命来看，由大到小依次为供应商2、供应商3、供应商1、供应商4和供应商5。根据可靠度函数定义，参数β和η决定了曲线的形状，两者值越大，可靠性越好，可以作为评价供应商的参考指标。

5家供应商电能表的电池模块（M1）、显示模块（M2）和电路模块（M3）的概率密度曲线如图7～图9所示。

图7 5家供应商电池模块（M1）概率密度曲线图Fig.7 Probability density curves of battery modules（M1）from five suppliers

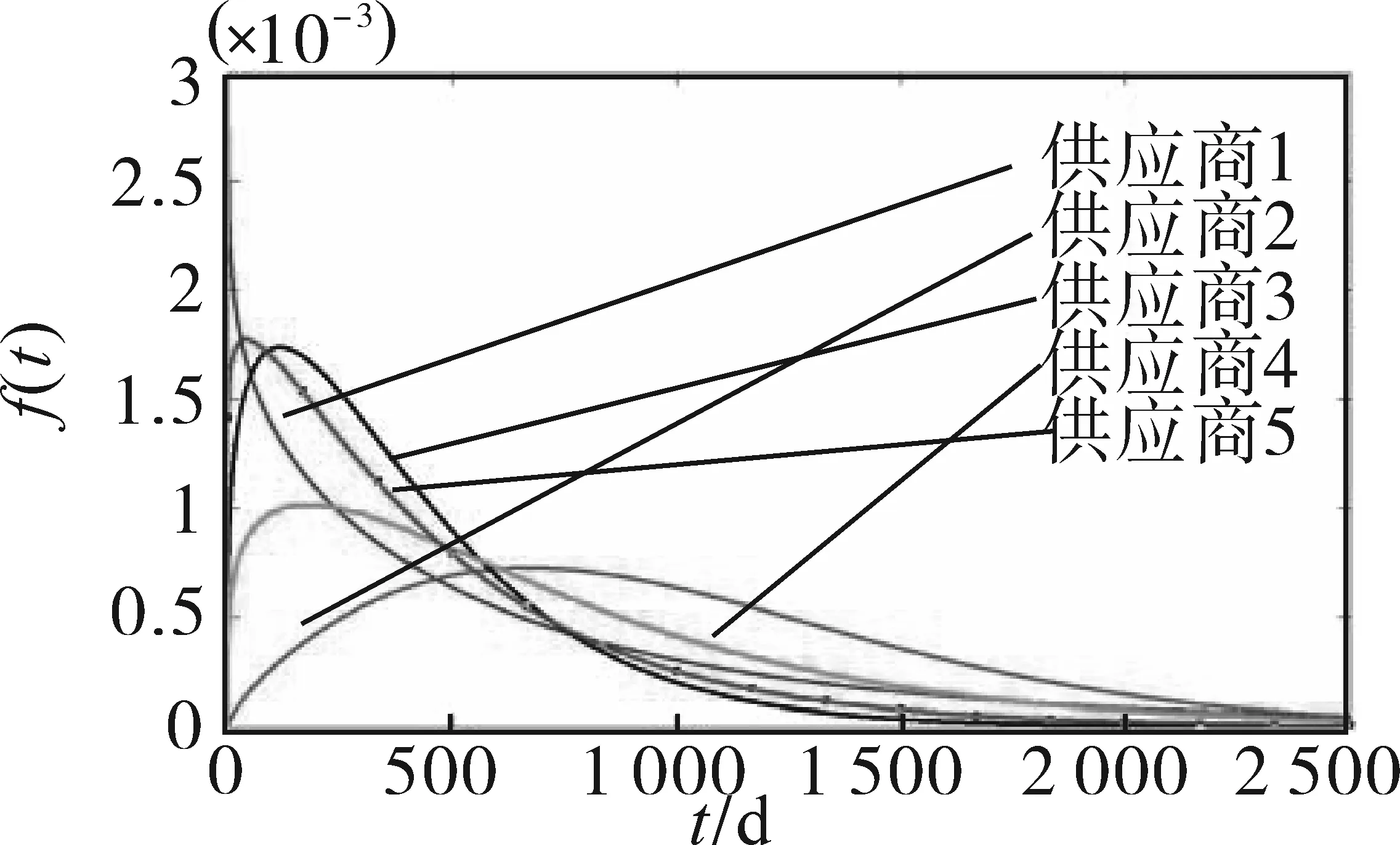
图8 5家供应商显示模块（M2）概率密度曲线图Fig.8 Probability density curves of display modules（M2）from five suppliers

图9 5家供应商电路模块（M3）概率密度曲线图Fig.9 Probability density curves of circuit modules（M3）from five suppliers

从子分布权重系数来看，大多数供应商电能表的电池模块在3种故障中所占权重极高，供应商1～供应商4的电能表故障主要发生于电池模块，而供应商5主要发生于电池模块和显示模块。从图7可以看出，5家供应商电池模块（M1）的失效概率密度曲线与电能表整体的失效概率密度曲线十分接近。从电池模块（M1）的性能角度来看，从优到劣依次为供应商2、供应商3、供应商1、供应商4和供应商5，与电能表的平均寿命情况一致。

由图8可以看出，除供应商2外，其他4家供应商的显示模块（M2）故障均发生在电能表使用初期，在运行200 d内达到故障高峰。从显示模块（M2）的性能角度来看，从优到劣依次为供应商2、供应商4、供应商1、供应商3和供应商5。

由图9可以看出，与显示模块（M2）类似，除供应商2外，其他4家供应商的电路模块（M3）在电能表运行初期很短时间内达到故障高峰。从电路模块（M3）性能角度来看，从优到劣依次为供应商2、供应商4、供应商1、供应商3和供应商5。

通过以上分析可知，无论从电能表整体性能还是单一模块性能来看，供应商2均表现最佳，供应商1中等，而供应商5最差。供应商3的电池模块性能较好，但电路性能较差，供应商4情况与之相反。因此，各供应商在着重提升电池性能的基础上，还要适当有针对性地改进薄弱模块性能，以使得电能表整体性能得到有效提升。

3 结论

本文通过故障树分析法提取电能表故障发生频率最高的3项故障，并利用混合威布尔分布对此3项电能表故障数据失效过程进行有效建模，得到了电能表的可靠度函数，最终计算出平均寿命。结果表明，09版电能表在2.5 a后进入故障高发期，平均寿命约为1 036 d，制约寿命的主要原因是电池故障。通过将模型参数作为评价指标，对比多家供应商产品的可靠性，可以为供应商产品改进提供方向。