中国国债收益率曲线的拟合及预测研究

牛晓健,邓昕妤

(1.2.复旦大学 经济学院,上海 200433)

引言

目前,随着我国利率市场化改革的不断推进和金融创新的不断深入,国债的价格形成及其收益率曲线的完善在利率定价中的地位越来越重要。从2018年8月17日,两年期国债期货合约在中国金融期货交易所正式挂牌交易,到2019年5月16日,中国金融期货交易所正式启动国债期货的做市交易,国债的现货和期货市场受到机构投资者的广泛关注,交易品种变得越来越丰富、越来越复杂。随着国债市场的丰富与发展,利率风险、信用风险等方面的风险管理也变得越来越重要。因此,提高对国债收益率曲线变化方向和形状的预测精准度,对债券市场投资者进行利率风险管理,以及对人民币利率体系的构建和完善有重要的意义。

现有的研究从两个维度考察收益率。第一个维度是以时间为横坐标轴,以某个到期期限的收益率为纵坐标轴,则连接各个收益率的散点的曲线反映某个到期期限的收益率随时间变化而变化的情况。从第一个维度看,研究某个固定的到期期限的收益率曲线更偏重曲线变化趋势及宏观影响因素分析。如果要对该收益率曲线做预测,则可以用时间序列方法研究一组历史收益率数据,通过检验,确定对该收益率影响较大的宏观因素,进而探索出在这些变量之间可能存在的一个长期稳定的变化关系,估计出反映该长期稳定变化关系的表达式,最后根据历史收益率值和宏观因素值,估计出收益率的预测值。

第二个维度是以不同的到期期限为横坐标轴,以收益率为纵坐标轴,则连接各个收益率的散点的曲线反映某时刻的不同到期期限的收益率的变化情况,或者是某时刻的利率期限结构。相比于第一个观察收益率的维度,利率期限结构更侧重于某一时刻不同到期期限的收益率水平的整体变动。比如,后一时刻的利率期限结构相比于前一时刻的利率期限结构的水平位置及形状的变化。从这一维度出发,对利率期限结构的预测通常需要基于一个假定的利率期限结构满足的函数表达式,估计出下期利率期限结构的函数表达式,在同一坐标系中画出函数图像,则得到下期的利率期限结构的曲线图。通常从这一维度出发的预测,相比于预测某个固定期限的收益率序列的下期值,更侧重于整个收益率曲线的形变,是一种相对位置的变化,而不是收益率值的绝对水平,或者说利率期限结构反映在水平位置上的变化。国内外的大量学者在该领域做出了较多研究,本文将对此进行评述。

一、文献综述

现代的有关研究理论主要可以按照对利率期限结构建立的模型分为静态模型研究理论和动态模型研究理论。

国外是最早开始研究静态模型理论的。对于静态利率期限结构理论早期的研究主要体现在构建拟合利率期限结构的数学模型方面。比较经典的模型或者拟合方法有息票剥离法和样条插值法。Fama et al.(1987)[1]提出息票剥离法在许多有关收益率曲线的拟合的研究中，常被用来作为获得初始的一组离散的到期收益率数据的第一步。除该方法以外,其他几种主要的静态利率期限结构模型本质都是采用某种函数作为样条基函数的样条插值法,但是这种方法的局限性在于需要估计的参数较多。基于简化模型的目的,Nelson et al.(1987)[2]提出了一类简约的利率期限结构模型——Nelson-Siegel模型,该类模型从曲线形状变化的角度考虑,实证表明该类模型可以较好地描述收益率曲线的形状特征。随后一些基于此模型的扩展形式的模型被不断地提出,形成了广受学术界和实务界应用的一大类参数模型。Svensson(1994)[3]扩展了Nelson-Siegel模型,增加了一项指数幂的形式到Nelson-Siegel模型表达式中,从而达到可以描绘出第二种跳跃的收益率曲线形状的目的。该模型被称为Svensson-Nelson-Siegel模型,即SNS模型。

国内对于静态利率期限结构模型的研究较晚。国内对于静态利率期限结构模型早期的实证研究主要集中于该模型在中国债券市场的应用性方面。朱世武 等(2003)[4]分别基于多项式样条法和Svenson-Nelson-Siegel模型,在依据最小定价误差的设计准则下,拟合了利率曲线,并且结合实际情况,得出结论为后者更适合拟合我国的国债即期利率曲线；并且利用更多数据拟合多条即期利率曲线,进行主成分分析,得出结论为第一因子解释力度不够高,第二因子和第三因子解释度较高,因而指出应该根据利率的不同变化形式进行债券组合头寸的调整以规避市场利率风险。仝晓燕 等(2007)[5]利用B样条函数对国债即期利率曲线进行拟合,并且重新选择样本检验样本外拟合误差,发现该估计方法有着较好的拟合优度和稳健性。周子康 等(2008)[6]指出Nelson-Siegel模型具有不能完全反映利率的驼峰等形态的特点,且Svenson-Nelson-Siegel模型的拟合精度依赖于初值的局限性,因此提出对Svenson-Nelson-Siegel模型增加高阶项的NSM模型,并利用GRG2非线性最优化算法进行实证分析,最后发现该模型拟合精度好,克服了前两个模型的缺点,具有很高的适应性。

近些年,相关研究从扩展静态利率期限结构模型转移到了动态利率期限结构模型、模型拟合结果的解释以及收益率曲线在风险管理、产品定价上的应用研究。Vasicek(1977)[7]提出了可描述利率动态变化的Vasicek模型,给出了瞬时利率变化的微分方程。Cox et al.(1985)[8]提出了利率期限结构的CIR模型,即一个利率随机变动的平方根过程。另外,一些考虑宏观经济因素的动态利率期限结构模型被提出。Dewachter et al.(2006)[9]引入宏观经济变量——通货膨胀、产出缺口、实际利率，建立了仿射利率期限结构模型,拟合出收益率曲线。Diebold et al.(2006)[10]在Nelson-Siegel模型的基础上,构建一个三因子的动态利率期限结构模型的框架来解释拟合结果,发现三个时变的参数可以被解释为水平、斜率和曲度因子。Singh et al.(2018)[11]基于Nelson-Siegel模型拟合利率期限结构,将计算得到的模型系数按照水平、斜率和曲度的方式进行解释,并且将其与宏观变量建立向量自回归模型,最后发现宏观经济变量的冲击对收益率曲线有显著影响。吴启权(2007)[12]通过动态Nelson-Siegel模型和动态Svenson-Nelson-Siegel模型拟合我国银行间债券市场的即期利率数据,同时进行样本外模型优度检验,发现两者效果都很好,但后者效果更好。陈映洲 等(2015)[13]利用息票剥离法对国债交易数据进行处理,计算得到即期利率数据,并用动态Nelson-Siegel模型和动态Svenson-Nelson-Siegel模型进行收益率曲线的拟合,发现后者的拟合精度和预测能力更优越。廖媛(2015)[14]利用动态Nelson-Siegel模型和动态Svenson-Nelson-Siegel模型进行收益率曲线的拟合,最后发现后者效果更好。

收益率曲线的预测对于宏观调控和风险管理都有着重要的意义。对于收益率预测的实证研究主要集中在如何利用已有利率期限结构模型进行预测、考虑加入宏观经济变量后的利率期限结构模型的预测及其精度和基于各种不同预测方法的利率期限结构模型的预测及精度等方面。

较早的有关利率期限结构模型预测方面的研究主要有Diebold et al.(2006)[15]在提出建立动态Nelson-Siegel模型后,利用AR(1)模型对拟合的利率期限结构的系数进行时间序列预测分析。Almeida et al.(2009)[16]把需要预测的系数考虑成向量并建立VAR模型,得出利用VAR模型预测的效果比单个系数进行AR(1)模型预测的效果好的结论。Pooter et al.(2010)[17]发现引入宏观经济变量的利率期限结构模型预测效果更好。另外也有学者考虑引入一些新的预测方法。Laurini et al.(2010)[18]在Diebold et al.(2006)[10]提出的模型的基础上,加入Svensson(1994)[3]在Nelson-Siegel模型中增加的一项,提出利用基于马尔可夫链的蒙特卡洛模拟法(Marcov Chain Monte Carlo,MCMC)对利率期限结构进行预测。神经网络算法被广泛地应用在金融和经济领域的相关预测研究中,而国外对于这个算法的应用大部分集中在股票市场。Patra et al.(2017)[19]利用多种神经网络预测方法——Artificial Neutral Network(ANN)、Mulrilayer Perceptron Model(MLP)、Radial Basis Functional Network(RBFN)对股票指数进行预测。还有些学者考虑采用贝叶斯预测法方法来进行利率期限结构的预测。周荣喜 等(2014)[20]考虑到先前相关的研究都仅局限于单一模型,因而从系统角度出发,考虑用组合预测的方法,依据利率期限结构模型构建中市场价格与理论价格偏差，利用平方法求解达到最小偏差的方式，确定组合模型中各模型权重系数,经过遗传算法的求解过程,对实际数据进行实证分析,同时比较多项式样条插值法、指数样条插值法、Nelson-Siegel模型和Svenson-Nelson-Siegel模型做拟合的结果,得出结论为组合模型的拟合效果最好。

二、利率期限结构的拟合

本文采用动态Nelson-Siegel模型(以下简称为动态NS模型)来拟合收益率曲线。原因有如下三点：第一，动态NS模型的系数可以有很好的经济解释；第二，动态NS模型具有简单直观的形式；第三，动态NS模型适合对收益率作出预测,再经过一定的计算过程,预测出收益率曲线。

Nelson et al.(1987)[2]提出Nelson-Siegel模型的表达式为：

y(0,t)=β0+β1(1-e-γτ)/γτ+β2((1-e-γτ)/γτ-e-γτ)

(1)

上述表达式(1)反映的是静态的利率期限结构模型。而Diebold et al.(2006)[10]通过研究静态的利率期限结构模型发现,如果把模型中的三个因子看成是时间的函数,即三条时间序列,那么就把静态的利率期限结构模型动态化了。他们提出的动态的利率期限结构模型具有如下形式：

f(t,τ)=β0t+β1t(1-e-γτ)/γτ+β2t((1-e-γτ)/γτ-e-γτ)

(2)

在上述模型表达式(2)中,一共有四个参数：β0t、β1t、β2t和γ。对四个参数的含义作出如下具体分析：

第一,当利率期限趋于无穷大时,即期利率趋于β0t,因此,β0t意味着长期利率水平。从经济学意义上看,该参数因子被命名为长期因子,或者被称为水平因子。

第二,参数β1t在模型中的载荷为(1-e-γτ)/γτ。随着利率期限的增大,该载荷函数由1开始快速衰减至0。也就是说,参数因子β1t仅在期限较短时对整体的利率水平有影响。因此,β1t可以看成是长短期利率的差值。从经济学意义上看,该参数因子被命名为短期因子,或者是斜率因子。

第三,参数β2t在模型中的载荷为(1-e-γτ)/γτ-e-γτ。随着收益率期限的增大,该载荷函数由0开始先增加随后衰减至0。也就是说,参数因子β2t在中期期限区间上对整体的收益率水平有影响。当期限过短或者过长时,该参数因子对整体的收益率水平几乎没有影响。因此,β2t主要反映的是收益率曲线的弯曲水平。从经济学意义上看,该参数因子被命名为中期因子,或者是曲度因子。

第四,参数γ是整个利率期限结构模型中的调参参数,主要调节的是中期因子水平和长期因子水平的衰减速度。因此,调参参数γ又被称为衰减因子。

(一)静态拟合

静态拟合即是针对表达式(1),利用MATLAB等编程软件中的非线性最小二乘法函数对样本数据做拟合,估计出模型表达式中的所有参数值,包括线性和非线性参数。非线性最小二乘法是基于误差平方和最小化的原理,因为对于每一个t时刻的样本,它是单独估计四个参数值的。该方法的优点是简单直观,可以保证拟合的精度。但是,该方法也存在一定的缺点。主要是由于非线性特征,并且因为过于考虑精度,模型拟合出的曲线可能并不光滑。

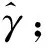
(二)卡尔曼滤波法

非线性最小二乘法是基于误差平方和最小化的原理,而本部分所述的卡尔曼滤波法是基于对数似然函数最大化的原理。卡尔曼滤波法的优点是能够获得比基于误差平方和最小化的估计结果更加稳定的估计结果。用卡尔曼滤波算法可以计算出合适的动态Nelson-Siegel模型中的衰减因子值[14]。

卡尔曼滤波法的基本原理是将一个动态的系统表示为状态空间,通过对预测误差进行分解,从而计算似然函数,进行似然函数最大化的求解,得到估计结果。其基本思想是迭代,即通过当期观测计算出下一期的状态变量,从而估算出下一期的观测值,并计算误差水平,如此过程反复迭代,直至误差调整至给定水平以下,完成整个迭代过程。

(三)拟合结果

本文采用的是三因子的动态Nelson-Siegel模型,因为动态的利率期限结构模型要求一个固定的调参参数,因此本文的拟合步骤如下：

1.利用非线性最小二乘法对观测数据基于静态的利率期限结构模型做出拟合。

2.基于静态利率期限结构模型的拟合结果,计算出利用卡尔曼滤波法迭代所需的各个参数的初值。

3.利用卡尔曼滤波法对观测数据进行动态的利率期限结构模型的拟合。由于动态利率期限结构模型的拟合需要一个固定的调参参数γ的值。因此,把γ作为变量,寻找出使对数似然函数最大的最优的γ。

4.基于固定的γ的值,利用最小二乘法对动态的利率期限结构模型中的三个剩余参数做拟合。当γ的值固定时,该模型其他三个参数是线性参数。因此,此时拟合出的结果,即拟合出的收益率曲线是比较光滑的。

本文采用的收益率数据来自中国债券登记结算有限公司,其主要原理是利用Hermite三次多项式进行插值，获得平滑的收益率曲线。选取的数据全部来自wind经济数据库中利率数据板块的中债国债即期收益率数据,时间频率为月频。选取的样本的时间区间为2009年1月至2018年12月。所选期限为18个期限,分别为1个月、2个月、3个月、6个月、9个月、1年、2年、3年、4年、5年、6年、7年、8年、9年、10年、15年、20年和30年。

本文利用上述方法拟合得到的最终结果如表1及图1—图4所示。

表1 动态Nelson-Siegel模型最终拟合结果的描述性统计分析表

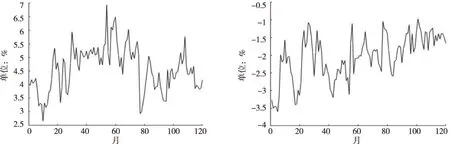
图1 最终拟合的水平因子变化 图2 最终拟合的斜率因子变化

图3 最终拟合曲度因子变化 图4 拟合的收益率曲线

三、国债收益率曲线的预测

(3)

将该函数的图像画出,则是预测的收益率曲线的图像。随着时间的变化,可以在获取新的数据后,再向后作出一步预测,则可以动态地做预测。本文通过以下动态神经网络方法对三因子序列做出预测。

(一)动态神经网络方法的理论

神经网络方法是机器学习领域中一个备受关注的算法。其主要思想是模拟人脑神经网络的拓扑结构,对数据也建立相似的结构。如果把神经网络方法看成一个黑箱子,那么算法的输入是观测数据,输出便是由观测数据经过不同网络层的调整,结合不同的权重和已经给定的映射函数计算出来的结果。

NARX神经网络的结构包括三层,即输入层、隐藏层和输出层。在构建一个NARX神经网络时,每一层都有需要考虑的因素,具体如下：

1.输入层,需要考虑输入层的节点数。一般输入层的节点数等于输入层的变量数。由于本文是对第三部分拟合得出的最终的三个因子序列分别做预测,因此输出层的节点数目由每个因子序列的自相关函数图像确定,也就是使某个因子序列的网络结构输入层的节点数等于第一个使该因子序列的自相关值接近某一水平的阶数。

2.隐藏层,需要考虑隐藏层的数目。通常而言,对于一个较为复杂的非线性数据序列,适当增加隐藏层的数量可以提高拟合精度,但是会降低拟合效率和拟合速度。因此,本文拟打算从一个隐藏层数目开始,通过预测,获取预测结果的精度,并且逐渐增加隐藏层数量,直至预测结果的精度无明显增加为止。

3.输出层,需要考虑输出层的节点数。这里,输出层就是当期的因子值,因此输出层的节点数为1。

4.权值的学习算法。由于存在反馈机制,网络结构根据输出的变量与实际的误差向前调整各层中的权重时,也存在一个学习算法。通常,MATLAB编程软件中给出了几种算法,包括：trainlm、trainbr和trainscg等。在计算速度方面,trainlm是最快的,trainscg稍慢,trainbr最慢。

5.输出的评价函数。输出的评价函数通常指一个输出的精度准则。本文采取最典型的MSE函数作为权值调整的依据,即在建立一个封闭的神经网络机制中,需要将权值调整到使输出的MSE值最小的状态。

(二)不考虑宏观变量的预测结果

动态神经网络方法的特点之一就是可以利用一组历史数据作为输入,在经过一个黑箱子后,得到输出。也就是说,在利用动态神经网络方法做预测时,是可以仅利用需要预测的变量本身的历史数据作为输入的。

其次,隐藏层的选取并没有较好的统一标准,适当增加隐藏层数量可以提高预测精度但是会降低预测速度。因此,隐藏层数量的设定需要在精度和效率之间做一个权衡,本文最终选定的隐藏层数目是3。

最后,本文利用这三种算法都进行了建模预测,选取了精度最高的trainscg算法。

(三)考虑宏观变量的预测结果

本部分采取的输入变量包括7种不同期限的上海银行间拆放利率(shibor)、汇率、社会融资规模和M2。其中,7种不同期限的上海银行间拆放利率(shibor)分别是1w shibor、2w shibor、1m shibor、3m shibor、6m shibor、9m shibor和1y shibor。汇率是美元兑人民币的平均汇率。社会融资规模采用wind数据库中的社会融资规模的当月值。在代入神经网络模型时,社会融资规模和M2的数据均采取自然对数处理。所有数据均来自wind数据库中的中国宏观数据库。

图5 基于不考虑宏观变量的预测模型的水平因子序列预测 图6 基于不考虑宏观变量的预测模型的斜率因子序列预测

图7 基于不考虑宏观变量的预测模型的曲度因子序列预测 图8 基于考虑宏观变量的预测模型的水平因子序列预测

图9 基于考虑宏观变量的预测模型的斜率因子序列预测 图10 基于考虑宏观变量的预测模型的曲度因子序列预测

(四)结果对比

本部分的结果如图5—图10所示。在判定预测精准度方面，如果考虑各个期限上的收益率值的预测精准度，那么由于一条收益率曲线的期限众多，计算起来较为困难。因此，可以考虑一整条收益率曲线的相对位置的精准度。针对这一点,本文拟构建一个交易策略,通过策略的收益结果判断哪个预测方法更好。

本文拟构建一个斜率交易策略,策略思路是：

第一,在t时刻,在以到期期限为横坐标轴、收益率为纵坐标轴的坐标系中,先画出t时刻的实际收益率散点数据连接的折线图。该实际收益率数据就是来自wind经济数据库利率数据板块的中债国债即期收益率数据。并且,根据前面的预测结果,在同一张图中画出预测的t+1时刻的收益率曲线的图像。

第二,根据上一步中所画出的两条收益率曲线的图像,寻找曲线斜率变化最大的一段区间,利用“高买低卖”的原则选择交易点和交易方式。

第三,设置一段时间为交易持仓时间,在持仓到期后,对前期交易的仓位进行平仓。这里,设置持仓时间为1个月,即从t时刻至t+1时刻。

第四,到了t+1时刻,重新按照第一、第二和第三的方式选择交易点和交易方式。

第五,若干个时间段后,计算每次交易的收益和累计收益,画出累计收益曲线。

以某个月的预测为例,根据下图11,表示在2019年2月的时刻,2019年2月的实际收益率曲线和2019年3月的预测的收益率曲线。根据上图3所示,预测的收益率曲线反映到期期限1月至到期期限5年的区间内,预测的收益率曲线的斜率有下降。那么,交易方式为做多1月期和5年期的收益率的价差。在2019年3月,做空1月期和5年期的收益率的价差。

图11 2019年2月实际的收益率曲线及未来一月预测的收益率曲线

本文设定每个月的交易持仓时间为1个月,并且以到期收益率为标的估计策略的收益结果。在做了12期的交易以后,下图是两种预测方法下策略的累计收益结果。根据图12、图13可知,第一种预测方法的效果更好。

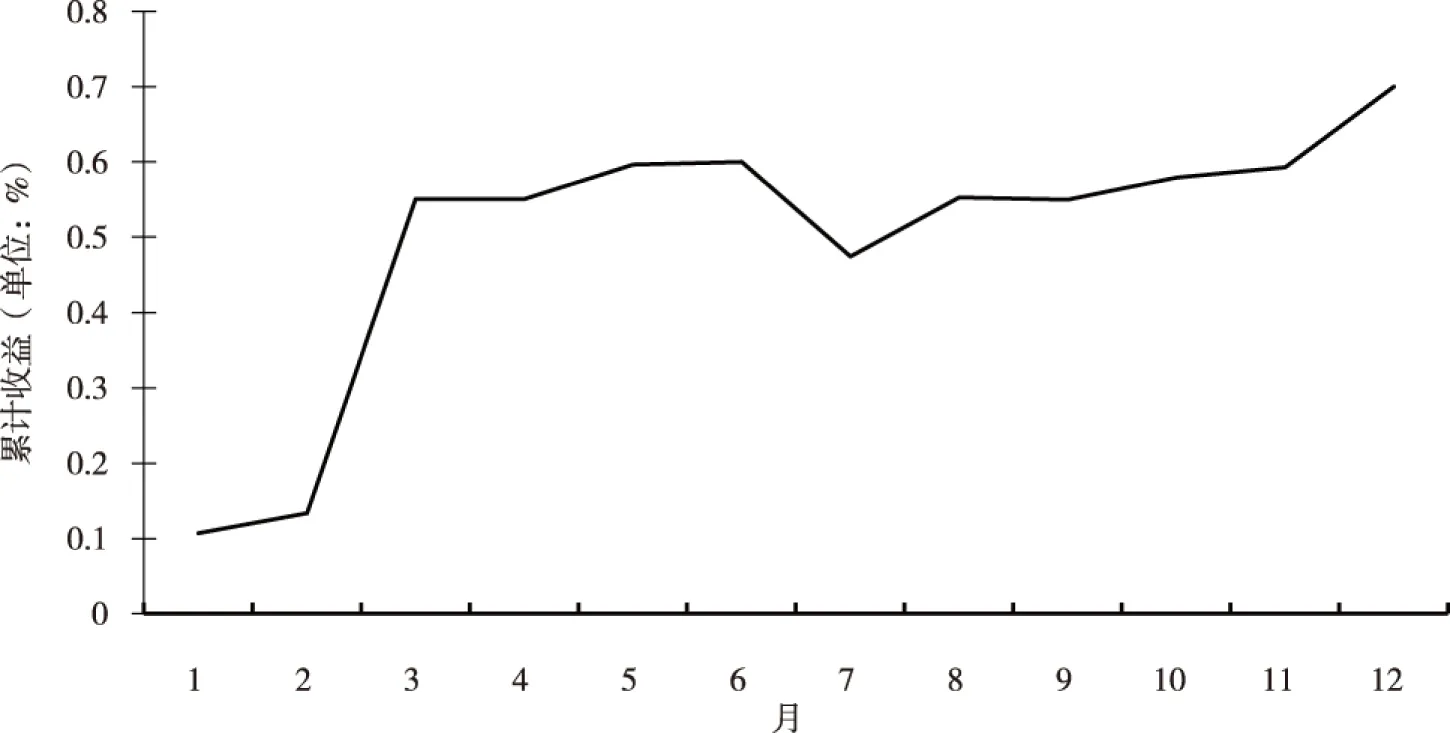
图12 基于考虑宏观因素的预测模型的时效斜率效益策略的累计收益曲线

图13 基于不考虑宏观因素的预测模型的时效斜率效益策略的累计收益曲线

四、结论与政策建议

本文采用了经典的动态利率期限结构模型—Nelson-Siegel模型对2009年1月至2018年12月的月度国债即期收益率数据进行拟合。本文通过两步法拟合得出的主要结论是：第一,动态NS模型确实可以比较好地拟合出收益率曲线；第二,仅用简单的静态拟合的结果是非常不稳定的,此时卡尔曼滤波法是一个很好的优化结果的方法。

本文利用NARX动态神经网络方法对前面拟合出的三因子序列做预测。本文建立了两种方法——不考虑宏观变量的预测方法和考虑宏观变量的预测方法。通过构建一个小的策略,发现利用考虑宏观变量的NARX模型对动态Nelson-Siegel利率期限结构模型中的三个参数做预测,并基于预测的参数值,再次代入模型表达式,得到预测的收益率曲线满足的函数表达式的方法是比较有效的。

研究结果表明该方法较好地预测了国债收益率曲线的变动规律,具有一定的应用价值。加入宏观变量对收益率曲线做预测时,效果更好。因此,利用本文的预测方法,可以考虑根据预测的收益率曲线与当前的收益率曲线的相对位置的变化,利用利率曲线交易的原理,寻找到有交易机会的曲线段,选择斜率交易策略或者蝶式交易策略进行投资。以蝶式交易策略为例,不再紧盯一个固定的期限价差的走势变化,而是在每一期,都寻找当期的有走势变化的期限,并且在当期做出相应的投资,比较符合时效的变化。该结论可为金融机构进行利率风险管理提供一定的参考。