基于应变指标的梁式桥损伤程度定量方法

王艺霖，王顺尧，李广宁

（山东建筑大学，山东 济南 250101）

0 引言

及时有效的损伤识别是桥梁安全运行的重要保障。桥梁的具体损伤情形有多种，但在理论上一般可把损伤对结构的影响用结构局部刚度的变化来代表［1-2］。损伤识别的基本方式是寻求合适的结构性能指标作为损伤识别指标，通过指标值的变化来发现损伤的位置和程度信息。

目前常用的损伤识别指标有静力位移［3］、静力应变［4］、频率［5］、振型［6］、应变模态［7］、曲率模态［8］、静态应变能［9］、频率响应函数［10］等。其中静力应变指标具有量测简单、精确度高的优点，值得特别关注。早期的基于静力应变指标的损伤识别方法已取得良好的效果，但从进一步完善损伤信息、增强对微小损伤敏感性等角度出发，仍在不断地推出改进方法。例如，采用光纤光栅应变传感器来获取更为精确的输入数据［11-12］，与神经网络等智能算法相结合［13］，基于宏观应变理论进行细微损伤的识别［14］等。

本文以更简便有效地实现损伤程度定量化为出发点，针对量大面广的梁式桥（简支梁和连续梁桥），同时采用两种静力应变指标（对应于弯矩的弯曲正应变、对应于剪力的剪切应变）来反映损伤引起的主梁局部抗弯刚度变化，探讨建立相应的损伤程度定量化方法。

1 基于应变指标的损伤程度定量方法

简支梁和连续梁桥的主梁一般承受外荷载、若干支座反力的作用。支座反力可近似为集中荷载，若外荷载也为集中荷载，则主梁上承受的都是集中荷载作用。在各集中荷载作用点之间的区域内，弯矩都将呈线性分布、剪力呈常数分布。

当损伤出现之后，这个规律将被打破，可据此识别出损伤的出现和位置，并有望获得损伤程度的定量信息。下面分别基于弯曲正应变指标、剪切应变指标进行损伤定量化的具体分析。

1.1 基于弯曲正应变指标的损伤程度定量方法

主梁正截面上某处的弯曲正应变计算式为：

式中，M 为所受的弯矩；y 为该处到截面中性轴的垂直距离；E 为弹性模量；I 为截面惯性矩。

当主梁状态完好时，各正截面的EI 值相等。根据式（1），各截面上y 值相同位置的ε 值沿主梁纵向的分布规律，将和弯矩M 的分布规律（线性分布）一致。而当主梁发生材料损伤导致弹模E 变化或截面出现几何损伤导致惯性矩I 变化后，各截面上y 值相同位置的相应ε 值就会发生变化，沿主梁纵向的分布规律将不再符合线性分布。根据此原理可进行损伤识别操作：

（1）在主梁上沿纵向以尽量小的间距布置应变传感器，传感器在各正截面内的位置相同（y 值相同）。

（2）在主梁上某处施加一集中荷载，测定各传感器的应变值（ε 值），然后考察各集中荷载（含支座反力）作用点之间区域内的ε 值沿主梁纵向的数据状况：如果各区段内的ε 值分布符合线性规律，则说明没有损伤出现；如果某测点的ε 值数据不符合这一线性规律，则说明该处出现了损伤。

（3）损伤程度的确定。首先假设主梁抗弯刚度在损伤区域内由EI 变成了aEI，求解出a 值即确定了损伤程度。根据式（1），由于y 和EI的取值一定，未损伤区域内实测到的各测点ε 值应符合线性分布。假设在主梁的A 点处出现了损伤，则A 点及周边测点的ε值分布情况将如图1所示。

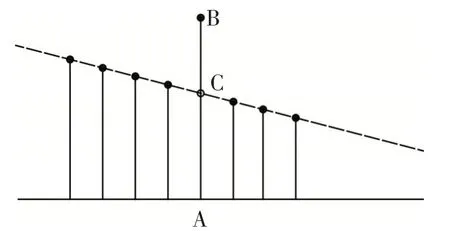
图1 损伤区域附近各测点的ε值分布

A 测点的ε 值将不在周边测点ε 值连成的直线之上，而是在B 处。周边测点ε 值连成的直线与AB 点的连线相交于C 点，则根据式（1）和比例关系可得：

式中：lAC、lAB分别是线段AC、AB的长度。进而得：

求得a 值后即得到了损伤区域内的抗弯刚度aEI，进而确定局部损伤的程度。

1.2 基于剪切应变指标的损伤程度定量方法

目前剪切应变分布情况的解析计算结果只对简单截面（如矩形）的情况比较准确，因此剪切应变指标主要适用于主梁为矩形截面的情况。

在剪力Fs作用下，矩形截面的最大剪切应变τmax出现在中性轴上，其值为：

式中，Fs为所受的剪力；b、h分别为矩形截面的宽度和高度。

损伤识别操作方法如下：

（1）沿主梁纵向以尽量小的间距在各截面的中性轴上布置应变传感器以测定剪切应变τmax。

（2）在主梁上某处施加一集中荷载，测定各传感器的剪切应变值（τmax值），然后考察各集中荷载（含支座反力）作用点之间区域内的τmax值沿主梁纵向的数据状况：如果各区段内的τmax值符合常数规律，则说明无损伤出现；如果某测点的τmax值不符合这一常数规律，则说明该处出现了损伤。

（3）损伤程度的确定。材料损伤引起的E 变化或几何损伤引起的bh 变化对应于式（4）的分母项Ebh，首先可假设Ebh在损伤区域内变成了aEbh，求解出a值即确定了损伤程度。根据式（4），未损伤区域内实测到的各测点τmax值应符合常数分布。假设在主梁的A 点处出现了损伤，则A 点及周边测点的τmax值分布情况将如图2所示。

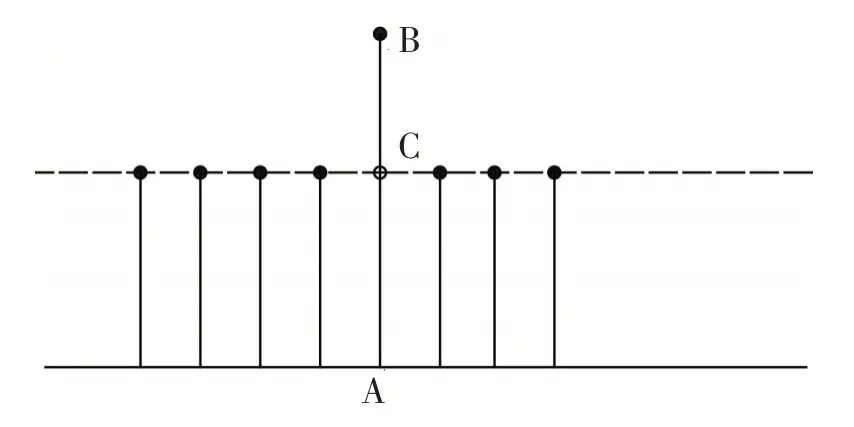
图2 损伤区域附近各测点的τmax值分布

A测点的τmax值将不在周边测点τmax值连成的水平线上，而在B 处。周边测点τmax值连成的直线与AB 点的连线相交于C 点，则根据式（4）和比例关系可得：

进而得：

求得a值后同样即得到了损伤区域内的抗弯刚度aEI，并可确定局部损伤程度。

2 应用实例

2.1 矩形截面简支梁桥（同时采用ε 和τmax 指标）

一跨度10m的简支梁桥，主梁采用C35混凝土和矩形截面（宽6m，高0.7m），弹模取为E=3.25e10N/m2，泊松比0.2。假定有两处损伤：（1）x=2m，y=0.2m，截面有效宽度减小为5.5m；（2）x=6m，y=0.2m，截面有效高度减小为0.5m。（x表示损伤区域左端到主梁最左端的距离，y表示损伤区域的长度，下同）

在跨中处（x1=5m，这里x1表示所研究截面到主梁左端的距离，下同）施加集中荷载F=1000kN，用MIDAS进行应变计算。

（1）基于弯曲正应变的损伤识别及程度量化

主梁各正截面的弯曲正应变增量如图3 所示。可以看到在设定的两个损伤位置处出现了明显的应变增量突变，据此可发现损伤的位置。进而根据图3上的数值和式（3）可分别确定两处损伤的z 值：损伤（1）处，a1=lAC/lAB=0.917；损伤（2）处，a2=lAC/lAB=0.364。与设定的损伤情况一致。

图3 弯曲正应变增量图

（2）基于剪切应变的损伤识别及程度量化

主梁各截面的剪切应变增量如图4所示。根据图4上的数值和式（6）可分别确定两处损伤的z 值：损伤（1）处，a1=lAC/lAB=0.917；损伤（2）处，a2=lAC/lAB=0.714。与设定的损伤情况一致。

图4 剪切应变增量图

2.2 箱形截面简支梁桥（采用ε 指标）

某56m 长预应力混凝土简支梁桥，主梁采用C40 混凝土和单箱单室截面（截面高3.8m，宽2.6m，壁厚0.5m）。设定两处损伤：（1）x=10m，y=0.2m，有效宽度减小为2.5m；（2）x=30m，y=0.2m，有效高度减小为3.7m。

在跨中处（x1=28m）施加集中荷载F=1000kN。得到对应的弯曲正应变增量如图5所示。

图5 弯曲正应变增量图

由图5可见在两个损伤位置处出现了明显的应变增量突变，进而根据图5 上对应的数值和式（3），可分别确定两处损伤的z 值：损伤（1）处，a1=lAC/lAB=0.969；损伤（2）处，a2=lAC/lAB=0.932。与设定的损伤情况一致。

2.3 箱形截面连续梁桥（采用ε指标）

某五跨预应力混凝土连续梁桥（为5×50m），主梁采用C40 混凝土和单箱单室截面（高3m，宽6m，壁厚0.4m）。设定四处损伤：（1）x=40m，y=0.2m，有效高度减小为2.9m；（2）x=80m，y=0.2m，有效高度减小为2.8m；（3）x=125m，y=0.3m，有效高度减小为2.9m；（4）x=210m，y=0.2m，有效高度减小为2.8m。

在跨中处（x1=125m）施加集中荷载F=100kN。得到对应的弯曲正应变增量如图6所示。

图6 弯曲正应变增量图

从图6可见在4个损伤位置处出现了明显的应变增量突变。进而根据图6 上对应的数值和式（3）可分别确定四处损伤的z 值：损伤（1）处，a1=lAC/lAB=0.921；损伤（2）处，a2=lAC/lAB=0.845；损伤（3）处，a3=lAC/lAB=0.921；损伤（4）处，a4=lAC/lAB=0.845。与设定的损伤情况一致。

3 结论

本文拓展了弯曲正应变和剪切应变指标在识别梁式桥主梁损伤方面的应用，给出了确定损伤程度的具体方法及实例验证。主要结论如下。

（1）利用集中荷载作用下弯曲正应变沿主梁纵向的线性分布规律可确定局部损伤的量化程度，且适用于各种截面形式的主梁。

（2）利用集中荷载作用下剪切应变沿主梁纵向的常数分布规律可确定局部损伤的量化程度，主要适用于矩形截面的主梁。

（3）基于弯曲正应变和剪切应变指标的方法都具有原理清晰、计算简单、操作方便的优点。