基于LSTM神经网络预测低温热源动态特性

陈 薇 袁中原 高 波

基于LSTM神经网络预测低温热源动态特性

陈 薇1袁中原1高 波2

（1.西南交通大学机械工程学院 成都 610031；2.四川省建筑科学研究院有限公司 成都 610081）

低温热源的入口温度和质量流量在有机朗肯循环（Organic Rankine Cycle, ORC）余热回收系统中是非常重要的热力参数，为了研究动态响应情况下ORC系统参数对系统性能的影响情况，利用机器学习中的LSTM神经网络，将某工厂中实地采集的10059组逐时热源温度和流量作为样本进行训练和测试，得到训练精度要求下的神经网络，对低温热源的温度和流量进行逐时预测，结果表明，利用神经网络可以满足精度要求预测低温热源的逐时温度和流量，为后续搭建系统的动态响应控制系统奠定基础。

LSTM神经网络；低温余热回收；热源动态特性预测；时间序列预测

0 引言

由于世界经济的快速发展造成了能源紧张问题[1]，大量学者针对可再生能源进行研究，包括风能、太阳能、地热能以及低温余热利用等等。有机朗肯循环在低温余热回收方面具有很大的潜力，当前主要研究方向为综合考虑热源、冷源、工质和设备等等各个方面因素优化ORC系统，力求最大化系统的余热回收效率。Bahaa Saleh[2]等通过优化热效率比较了31种烷烃和氟化烷烃的循环性能，得到了不同有机工质使用的温度范围；2013年，Li等[3]针对温度低于150℃的低温热源，列举了适用于超临界ORC系统的有机循环工质的物性参数；韩中合等[4]选取了9种有机工质，研究了蒸发温度、蒸发压力和膨胀机功比对系统不可逆损失的影响。

目前以上的研究多是假定系统在稳态运行下进行研究，但是实际应用中热源的特性以及外界条件都是动态波动的，考虑热源波动条件下的系统动态响应及调节机制较为困难。近年来，由于神经网络具有良好的自适应性和处理非线性问题的能力被广泛用于实际中[5]，曾[6]等人基于神经网络遗传算法以翘曲变形和收缩为质量指标，对注塑模具工艺参数进行优化，并进行试验验证了神经网络模型的预测精确度；Li[7]等人搭建了BP神经网络、RBF神经网络的径向基神经网络预测风能利用系统的中的风速，并对三种神经网络的预测精度进行比较；Yang[8]等人通过搭建实验台并结合遗传算法优化的BP神经网络对ORC系统回收车用发动机余热系统的运行参数进行预测和优化，训练所得神经网络模型的预测精度都在5%以内，表现出了良好的预测能力；Szoplik[9]等人利用神经网络预测用户对天然气的需求量，研究结果表明，神经网络可以精确预测未来一年内某一天某一个小时的天然气消耗量。

本文应用长短期记忆神经网络（Long short-term neural network），以工厂实测的10059组逐时低温热源的入口温度和质量流量作为训练样本，训练得到要求预测精度内的神经网络模型，用于预测未来一个时间步长的低温热源特性，为之后的动态响应控制系统奠定基础。

1 LSTM神经网络

LSTM（Long-short time memory）神经网络是循环神经网络中特殊的一种，主要是为了解决循环神经网络中梯度消失和梯度爆炸的问题，可以根据历史数据的特性回归预测未来的数据或对数据进行分类，与BP神经网络不同的是，LSTM神经网络每一层神经元之间的传播不仅与前一层有关，还与之前的每一层的神经元都有关[10]。

如图1所示是一个前向传播神经网络的拓扑图，式（1～5）是具有一个隐层的三层前向传播神经网络的表达式。

图1 前馈神经网络拓扑图

（3）

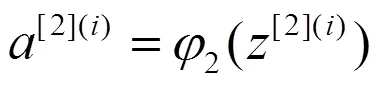
如图2所示是LSTM神经网络的拓扑图，LSTM模型在每一个单元A上都包含一个前向传播神经网络。LSTM单元A主要包括三个模块，遗忘、输入、输出过程，Ct其中代表单元的长期记忆，ht代表单元的短期记忆，Xt为每次外部输入的数据。长期记忆在每次进入LSTM单元进行训练时，遗忘一些不重要的信息，随后输入单元进行训练最后输出短期记忆ht，是Ct-1，ht-1，Xt的共同作用。

图2 LSTM神经网络拓扑图

1.1 输入参数和输出参数确定

在本文中，为了研究热源波动条件下系统的控制模型，实地采集了工厂中2019年1月1日20:00～2019年3月29日23:00的逐时热源温度和流量，通过10059组历史热源温度和流量数据对未来一个时间步长的数据进行回归预测。分别建立两个LSTM时序神经网络模型，模型的输入参数都是以时序作为单一变量，输出数据是热源的入口温度和流量。

由图3、图4可知，热源的温度和流量是逐时变化的，尤其热源的质量流量变化率较大，所以采用动态预测响应进行系统优化和控制是必要的。

图3 热源逐时温度

图4 热源逐时质量流量

1.2 神经网络模型搭建

1.2.1 求解器

求解器是在每次迭代过程中更新神经元的权值的算法，深度学习中的求解器主要包括标准梯度下降法（SGD）、动量梯度下降法（MSGD）、RMSprop和ADAM求解器。ADAM结合了Momentum和RMSprop梯度下降法，并且是一种极其常用的学习算法，被证明能有效适用于不同神经网络，适用于广泛的结构。

1.2.2 代价函数

损失函数叫做误差函数，用来验证算法的运行情况，Loss function: L(,)用于衡量预测输出值和实际值有多接近。

损失函数针对单个的样本，在深度学习中，使用代价函数表示参数的总代价，训练神经网络模型的过程就是找到合适的，使得代价函数的总价值降到最低。代价函数的表达式如式（6）所示：

1.2.3 正则化

在深度学习中，为了避免数据出现过拟合的现象，通常采用的方式有增大数据集和正则化，在进行深度学习的时候往往很难增加模型的数据集，获取数据集的成本也较大，所以一般采用正则化的方式来解决模型的过拟合现象。深度学习领域采用的正则化方式主要是L2正则化，其表达式如式（7）所示。

其中，是正则化参数，在本文中，正则化参数选择为1，阈值不使用正则化。

1.2.4 学习方式

根据神经网络模型中隐含层的数目，可以将机器学习方式分为浅层学习和深度学习，本文样本数据集较小，选用浅层学习方式。

1.2.5 权值初始化方式

在网络训练时，神经网络的初始权值和阈值决定了网络训练收敛速度的情况，本文初始权值生成方式均采用‘glorot’，初始阈值都设置成0。‘glorot’是正态分布初始化方法，也称作Xavier正态分布初始化，参数由0均值，标准差为sqrt(2/(fan_in+ fan_out)的正态分布生成，fan_in和fan_out分别为输入层和输出层的神经元数目，在本文中，即为0均值，标准差为1的正态分布生成神经网络的初始权值。

机器学习中常用的评价标准主要包括RMSE、MSE、MAE、MAPE[11]，本研究中采用的代价函数为方差MSE（Mean Squared Error）和均方根误差RMSE（Root Mean Squared Error）其表达式如式（8～9）所示：

1.3 训练过程

本文采用Matlab软件对LSTM神经网络进行训练，得到满足预测精度要求的神经网络对低温热源的热源温度和热源流量进行预测。编程训练流程如图5所示。

图5 LSTM神经网络训练流程图

由图3可知，热源温度波动较小，取样本数据的90%用训练温度预测神经网络模型，图4可知，流量波动较大，取样本数据的95%用训练温度预测神经网络模型，其余数据作为测试集验证神经网络模型的预测精度。

1.4 神经网络超参数

1.4.1 学习速率

学习速率是更新每次训练梯度下降的超参数，取值范围为0-1，本文初步设定学习速率为0.005进行训练，初始迭代最大次数为500次，在训练250次后降低学习速率，衰减因子为0.2。

1.4.2 隐层神经元数目

对于浅层神经网络来说，隐层神经元的数目要小于输入层权值和阈值的数目，隐层神经元数目过多会导致过拟合的现象增加网络训练时间，隐层神经元数目过少可能达不到训练精度，神经网络模型的训练误差较大。本文初步选用LSTM网络隐层神经元数目为100，根据训练的损失函数收敛情况和训练的时长调整神经元数目。

1.4.3 Mini-batch大小

选择单用CPU进行训练，考虑到电脑的储存和运行方式，一般选择2的n次方作为Minibatch的大小，本研究中LSTM采用Minibatch的初始大小为64，并在训练过程中尝试几个不同的2的n次方值，找到最佳的Minibatch大小值。

1.4.4 激活函数

激活函数主要包括隐含层激活函数和输出层激活函数，激活函数的主要作用是将各个神经元进行转换，而不是简单的线性加和，如果隐层的激活函数取线性函数，那么不论隐含层和隐含层的神经元数目有多大，从输入到输出都只是输入因子的线性映射。

深度学习中常用的激活函数以及优缺点和适用场合主要包括如表1所示。

表1 深度学习中常用的激活函数

图6 sigmoid函数

图7 tanh函数

神经网络LSTM层中，遗忘门和记忆门的激活函数是‘sigmoid’，0代表完全遗忘，1代表完全记忆，输入层输出层激活函数选择‘tanh’。

2 训练结果

经过多次反复训练，调整神经网络单元的隐层神经元数目、初始学习速率、学习速率衰减步数、Minibatch大小、最大迭代次数得到合适的神经网络模型。

2.1 预测热源温度神经网络模型参数

本文训练后用于预测热源逐时温度的LSTM神经网络模型参数如表2所示。

表2 预测热源温度神经网络训练超参结果

2.2 预测热源温度神经网络结果分析

图8 使用预测值更新网络预测热源温度

训练后的LSTM网络一次预测一个时间步，并在每次预测时更新网络状态，对于每次预测，使用前一次预测作为网络的输入，本文采用了两种方式更新每次预测的网络状态，第一种为利用神经网络每小时预测温度值更新网络，预测评估结果如图8所示，神经网络预测未来一个小时的相对误差都在2%之内；如果在更新网络的过程中，可以访问时间步长内的观测值，第二种方式为用观测值更新网络，预测结果如图9所示，预测相对误差都在2.5%之内。实际应用中，前一个小时的数据都是可以访问的，更符合第二种情况。

图9 使用观测值更新网络预测热源温度

由图8、图9测试集的评估表现可知，利用LSTM神经网络预测低温热源的动态温度是可靠的。

2.3 预测热源流量神经网络模型参数

本文训练后用于预测热源逐时流量的LSTM神经网络模型参数如表3所示。

表3 预测热源流量神经网络模型训练参数

2.4 预测热源流量神经网络结果分析

图10 使用预测值更新网络预测热源流量

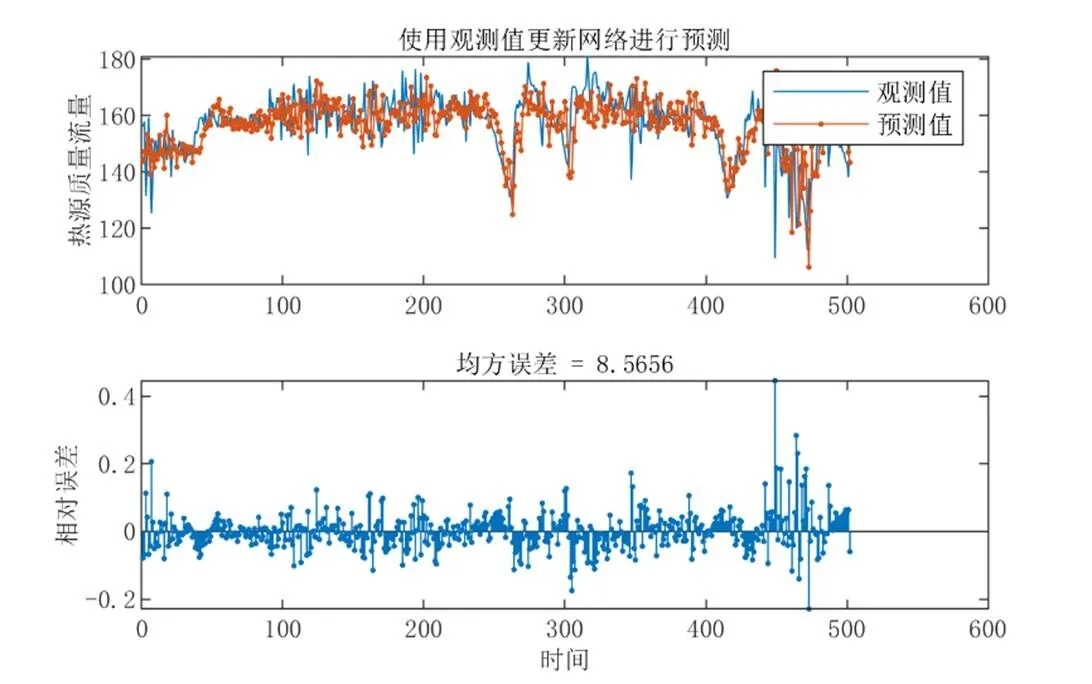
图11 使用观测值更新网络预测热源流量

本文采用相同的更新网络的方式预测评估网络预测精度，热源流量的逐时波动程度更大，第一种预测评估结果如图10所示，神经网络预测未来一个时间步长的相对误差大多都在25%之内；第二种预测评估结果如图11所示，预测相对误差都在25%之内，与温度同理，在实际应用中应使用观测值更新网络预测。

由图10、图11测试集的评估表现可知，利用LSTM神经网络预测低温热源的动态流量是可靠的。

3 结论

本文将实地检测的2019年1月1日20:00～2019年3月29日23:00的10059组热源逐时温度和流量作为LSTM神经网络的样本，配置初始神经网络超参数进行训练并根据预测精度、训练收敛情况、训练时长调整超参数最后得到合理的训练模型，得到以下结论：

（1）采用两种不同的网络更新方式更新训练所得的神经网络模型预测温度，结果显示，神经网络模型能准确预测低温热源的逐时温度，预测误差都在2.5%以内。

（2）采用两种不同的网络更新方式更新训练所得的神经网络模型预测温度，结果显示，神经网络模型能准确预测低温热源的逐时流量，预测误差大多都在25%以内，为后续ORC系统动态响应控制的研究奠定了基础。

（3）预测波动较小的热源入口温度，神经网络隐层神经元数目选择200时就可以达到较好的预测精度，但对于波动较大的流量预测，增加神经元数目还是不能达到非常小的预测精度，后续考虑用其他网络模型训练预测热源逐时流量。

[1] ZHAO G Y, LIU Z Y, HE Y. Energy consumption in machining: Classification, prediction, and reduction strategy[J]. Energy, 2017,133:142-157.

[2] SALEH B, KOGLBAUER G, WENDLAND M. Working fluids for low-temperature organic Rankine cycles[J]. Energy, 2007,32(7):1210-1221.

[3] LI C, BESARATI S, GOSWAMI Y. Reverse osmosis desalination driven by low temperature supercritical organic rankine cycle[J]. Applied Energy, 2013,102: 1071-1080.

[4] 韩中合,叶依林, 赟.不同工质对太阳能有机朗肯循环系统性能的影响[J].动力工程学报,2012,32(3):229-234.

[5] WANG H, LEI Z, ZHANG X. A review of deep learning for renewable energy forecasting[J]. Energy Conversion and Management, 2019,198:111799.

[6] 曾军亮,王荣吉,冯晓欣.基于神经网络和遗传算法的工艺参数优化[J].塑料,2013,42(5):106-109.

[7] LI G, SHI J. On comparing three artificial neural networks for wind speed forecasting[J]. Applied Energy, 2010,87(7):2313-2320.

[8] YANG F, ZHANG H, HOU X. Experimental study and artificial neural network based prediction of a free piston expander-linear generator for small scale organic Rankine cycle[J]. Energy, 2019,175:630-644.

[9] SZOPLIK J. Forecasting of natural gas consumption with artificial neural networks[J]. Energy, 2015,85:208-220.

[10] WANG J Q, DU Y, WANG J. LSTM based long-term energy consumption prediction with periodicity[J]. Energy, 2020,197:117197.

[11] HUANG L, WANG J. Global crude oil price prediction and synchronization based accuracy evaluation using random wavelet neural network[J]. Energy, 2018,151:875-888.

Prediction of Optimal Temperature for Organic Rankine Cycle Based on Artificial Neural Network

Chen Wei1Yuan Zhongyuan1Gao Bo2

( 1.School of Mechanical Engineering, Southwest Jiaotong University, Chengdu, 610031;2.Sichuan Institute of Building Research, Chengdu, 610081 )

As two important factors, input temperature and mass flow of heat source have great influence on the performance of ORC system. In this paper, we proposed a Long short-term memory (LSTM) neural network that can forecast intermitted and chaotic hourly temperature and mass flow of heat source. The temperature and mass flow data used are the hourly mean temperature and mass flow collected in one industry factory. And the two well trained neural networks are tested with the test dataset and used to forecast the next hourly temperature and mass flow of heat source. The results show that the proposed neural networks offer reliable forecast of the dynamic parameters of heat source, which indicates LSTM neural network can be used to build the dynamic controlling system in the future.

LSTM neural network; waste heat recovery; dynamic forecast of heat source; time series prediction

1671-6612（2020）06-670-06

TM617

A

四川省科技计划项目：基于分级冷却的工业余热高效能量回收系统（2019YFG0327）；四川省建筑科学研究院有限公司2018年度科研项目（四川省绿色公共建筑运行维护体系关键技术研究）

陈 薇（1996-），女，硕士研究生，E-mail：vchen@my.swjtu.edu.cn

袁中原（1983.8-），男，博士，E-mail：zhongyuan.yuan@home.swjtu.edu.cn

2020-10-25