考虑影响方式的雷达测高误差因素表征方法

王永攀，常春贺，苏号然，蔡志成

(空军预警学院, 武汉 430019)

未来信息化战争对雷达高度的测量提出了更精准、更稳定、更可靠的要求，如何提高雷达测高精度、减小测高误差已成为制约三坐标雷达作战效能发挥的重要研究问题。为此，一些专家学者或部队技术人员围绕雷达测高问题展开了大量的研究[1]。从研究情况来看，大致可以分为两类：一类是从测高原理角度出发，通过研究测高方法、改变系统设计等方面，力求从源头上降低测高误差，这些研究理论性强、方法新颖，但也存在技术应用滞后、改装推广迟缓、有待实战验证等问题[2-3]；另一类研究是从测高影响因素的角度出发，通过分析测高误差影响因素，寻求测高误差补偿方法，为降低测高误差提供参考借鉴，虽然贴合部队实际，但还存在因素分析不系统、误差表征不全面等问题[4-5]。上述两类研究对降低三坐标雷达测高误差均提供了较好的研究思路，但由于雷达测高误差受作战环境、操作使用等影响较大，系统分析了三坐标雷达测高误差影响因素，进而探索误差补偿方法，将是提高雷达测高精度研究进程中不能回避的课题。

关于雷达测高误差影响因素分析的研究，一些研究区分系统误差和随机误差等方面对测高因素进行了分析，但是没有对测高误差的表征进行系统分析[6-7]；还有一些研究从天线标定误差、测高体制误差、环境因素误差等等方面对多类误差因素进行了全面分析，并进行了数学表征，但是对各因素的影响方式考虑得还不够，后续进行误差补偿的针对性还不够强[8-9]。实际应用中，诸多因素对测高仰角的影响方式，一部分是直接的，一部分是间接的，还有一部分是偶然的，比如说测高过程中遇到的高度突跳问题[10]。基于此，本文研究基于影响方式的雷达测高误差因素表征方法，为后续针对性开展测高误差补偿方法研究提供参考借鉴。

1 三坐标雷达测高误差产生机理分析

1.1 测高基本原理

现役三坐标雷达通常根据已经测定的目标距离和仰角，通过公式计算来确定目标的高度。目前，雷达测距技术已经逐步成熟，测距精度相对较高，因此，在测高过程中更重要的是对仰角的测量。关于测角的方法有很多，主要分为相位法和振幅法，其中，振幅法又分为最大信号法和等信号法。由于在技术与精度上的优势，等信号法在三坐标雷达中应用和研究较多，等信号法测角主要采用2个相同且彼此部分重叠的波束，其基本原理如图1所示[11]。

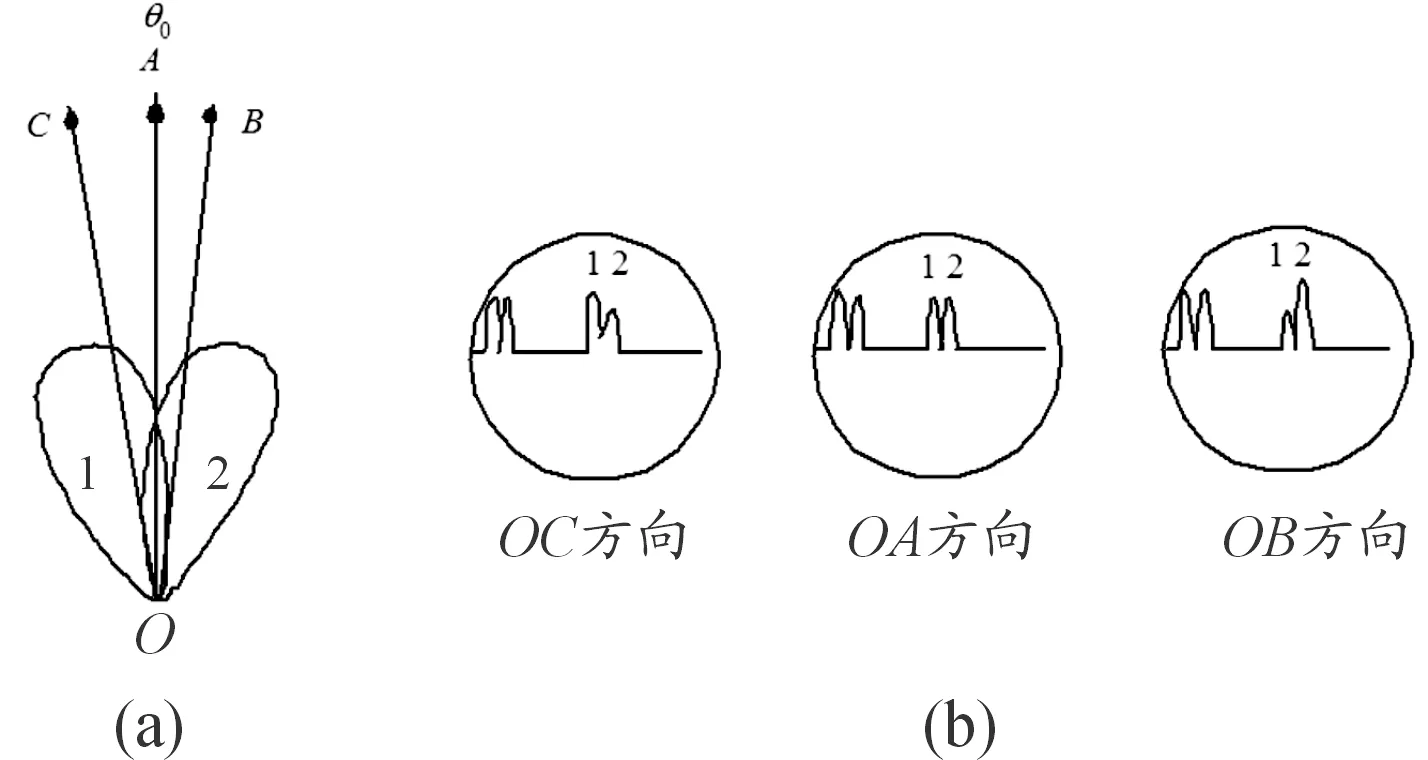
图1 等信号法测角基本原理示意图

图1(a)为2个相交的波束，图1(b)为K型显示器画面。图1中，若目标处于波束1和波束2相交的位置OA方向(等信号轴方向)，则两波束收到的信号强度相等；当目标处于OC方向时，波束2收到的目标回波强度比波束1收到的目标回波弱；当目标处于OB方向时，波束2收到的目标回波强度比波束1收到的目标回波强。通过比较2个波束接收到的目标回波信号的强弱就可以判断目标偏离等信号轴OA的方向，通过查表的方法来估算目标的偏离角。

为了提高测角精度，在等信号法测角的基础上，三坐标雷达常采用多波束比幅测高的方法。它的基本原理是多个波束同时接收目标回波信号，由于目标回波入射的接收波束位置不同，不同波束接收到的回波信号幅度也不同，通过对相邻信号的输出信号进行比较，就可以测量出目标的仰角[12]。图2给出了三波束比幅测高的基本原理。

图2中，3个接收波束j，j-1，j+1分别在同一个仰角面上，目标回波从OA方向进入，与接收波束等信号轴方向偏离Δθj。3个波束同时接收到目标信号，选择回波信号较强的2个波束(j，j+1)进行计算。设目标回波进入j和j+1波束的幅度分别为ui和ui+1，其幅度差值为Δu，且与偏离角Δθj成正比，通常满足：

图2 三波束比幅测高基本原理示意图

(1)

式(1)中，θ3 dB为接收波束半功率点波瓣宽度，即3 dB波瓣宽度。

可见，知道Δu就可以知道偏离角Δθj。实际应用中，通常把测得的Δu与Δθj的关系制成表，在计算出相邻波束的电压差值Δu后直接查表就可以求得Δθj。

在求得Δθj后，根据目标回波入射方向与相邻两波束等信号轴直接的位置关系，就可以求得如图2中的目标仰角θ为：

θ=θj-Δθj

(2)

1.2 影响测高误差的主要参数分析

三坐标雷达的高度是通过雷达与目标的斜距R、以及目标仰角θ计算出来的，其计算公式为：

(3)

式(3)中：Ha为雷达架高；re为地球等效半径，通常取8 490 km。

分析发现，影响目标探测高度的参数主要有3个，即Ha、R、θ。其中，雷达架高对测高误差的影响即雷达架高误差，其误差很小，可以忽略。这里只分析目标斜距R以及目标仰角θ对目标高度H的影响。

图3给出了目标斜距R在200～215 km变化、目标仰角θ在1°～4°范围内变化时目标高度的变化情况。

图3 H与R、θ的关系示意图

从图3可以看出，当θ=2°时，目标斜距R由207 km增加100 m时，目标高度增加9 m，即目标斜距误差为100 m时，高度误差为9 m；当R=207 km时，目标仰角θ增加0.02°时，目标高度增加75 m，即目标仰角误差为0.02°，高度误差为75 m。而三坐标雷达的测距误差往往小于100 m，因此，可以得出结论：仰角误差是引起测高误差的主要因素，这一结论在业内基本达成共识。下面涉及到的测高影响因素专指仰角误差的产生因素。

图4给出了某三坐标雷达在执行专机保障任务时采集到的测高实际数据。为了便于观察，图4中测高误差在原来基础上进行了5倍放大。

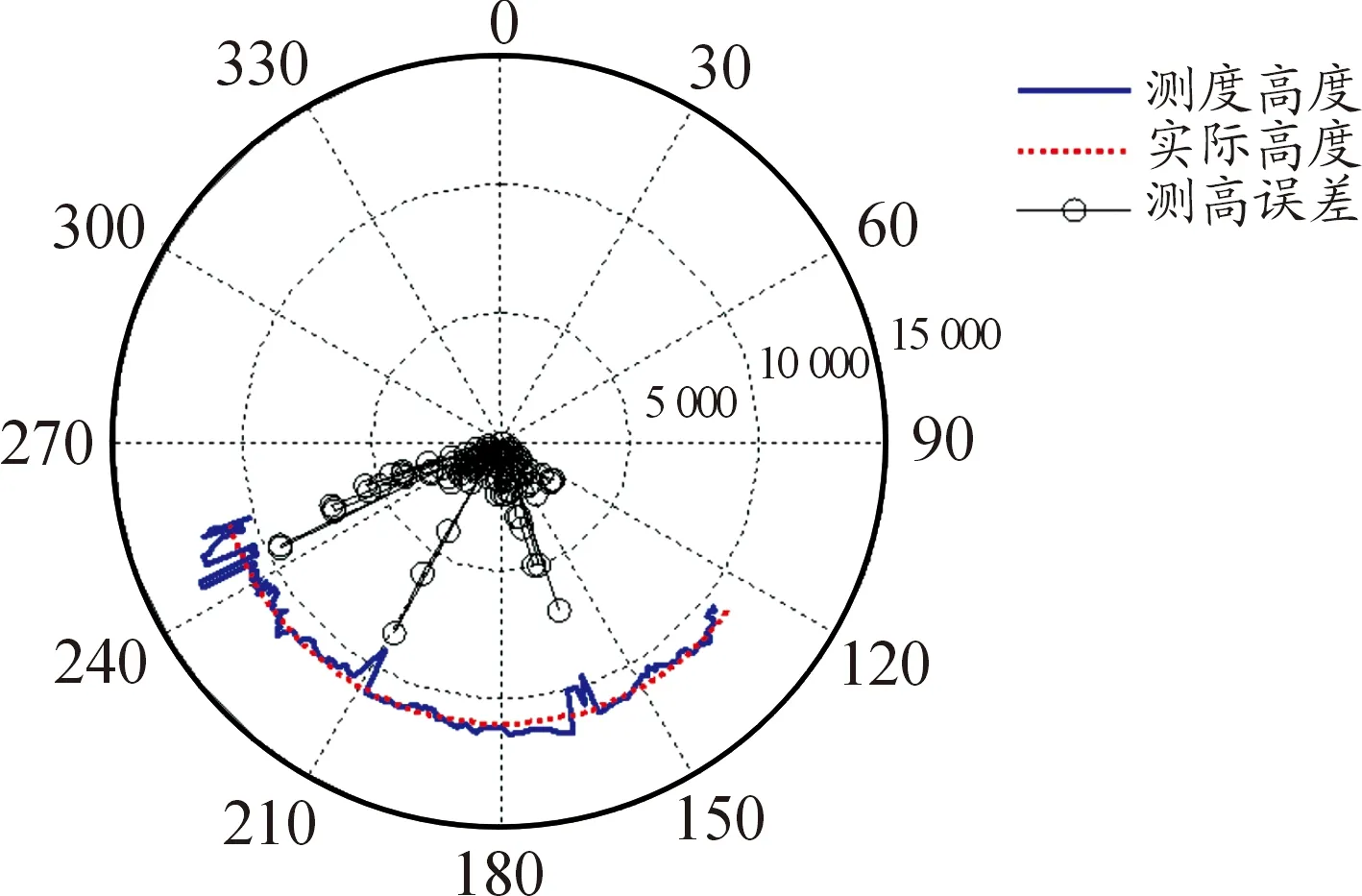
图4 雷达测高数据

从图4可以看出，在不同的方位上，雷达测高误差不同，这表明存在一定的因素在不同的方位上对雷达测高产生影响，称之为方向性误差。当然，还有一些不因方位而变化的测高影响因素，称为单向性误差。下面分这两个方面对测高影响因素进行具体讨论。

2 测高误差影响因素分析

2.1 单向性误差

2.1.1非标准大气折射误差σS

电磁波在传播时往往会受到大气层的折射作用，在进行雷达高度计算时，通常认为大气层是均匀的，用4/3倍地球半径代替地球的等效半径，将电磁波等效为沿直线传播，从而来校正大气折射对测高的影响。而实际上，大气折射是一个渐进变化的过程，其折射系数N随着高度的增加而呈现减小的趋势，通常有以下关系:

N(Ha)=N0exp(-0.143 86Ha)

(4)

式(4)中：N0为N在海平面的平均值，N0=313；Ha为雷达站高度。

由于大气折射的作用，雷达在测高时就会产生相应的仰角误差。图5给出了大气折射对雷达测高的影响示意图。

从图5可以看出，目标回波在经过大气折射后，产生了弯曲。雷达实际测量的仰角为θ，与实际仰角θr产生σS的仰角误差，且满足关系θ=θr+σS。从而使得实际测量目标位置高于实际目标位置，产生ΔHt的测高误差。仰角误差σS可通过下式计算得到[13]:

图5 大气折射对测高的影响示意图

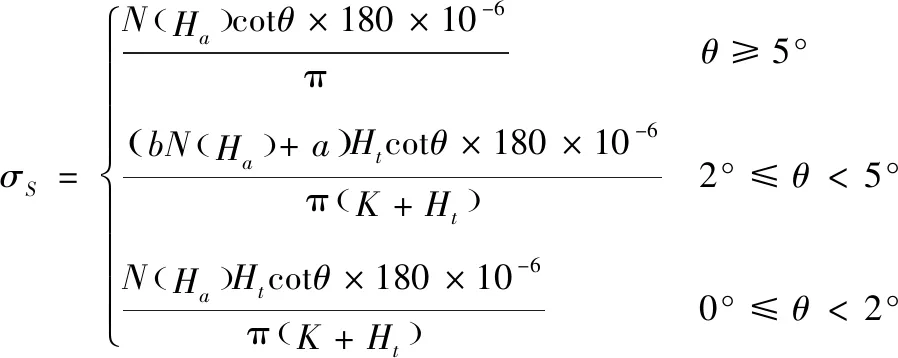
(5)

式(5)中：K为常数，取10.675 km。

2.1.2机内噪声误差σN

接收机内部噪声是无法避免的，为了更好地探测目标，就需要相应的回波信号有用功率来平衡，使得天线偏离目标一定的角度，从而引起仰角误差。当误差信号功率与噪声功率相消时，天线处于平衡位置。对于理想的接收系统，机内噪声误差为：

(6)

式(6)中：θ3 dB为仰角接收波束3 dB波瓣宽度；kp为单脉冲斜率，通常取kp=1.6；(S/N)p为脉冲检测信噪比；Np为脉冲数。

由于噪声是一随机起伏量，因此，由噪声引起的仰角误差也是一随机起伏量，也就是说噪声误差引起的测高误差是随机的，直接表现就是雷达测量的目标高度时高时低。

2.1.3接收通道幅度不一致误差θA

采用比幅测高体制的三坐标雷达通过计算相邻波束接收的回波信号幅度对数电压差值Δu后，直接查表求得回波入射位置θ与波束相交位置θb的偏离角Δθ，进而求得目标的仰角位置θ=θb+Δθ。因此，回波信号的幅度对确定目标仰角具有决定性作用。可见，保持各个接收通道的增益相等成为了测高的前提条件，当某一路增益出现偏差时，就会改变这一路信号原有的幅度，从而使得雷达测高数据偏离实际数据，使得Δu发生变化，产生测高误差。

一般来说，回波信号幅度差值Δu与偏离角Δθ呈线性关系，满足：

(7)

雷达在开机时会进行接收机校正，实际可以做到接收机增益比值σΔA=0.5 dB=1.06，此时产生的误差为：

(8)

2.1.4A/D量化误差σAD

A/D量化误差通常表示为:

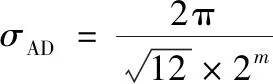
(9)

式(9)中，m为量化位数。

2.1.5角度量化误差σJ

角度量化误差σJ表示为:

(10)

式(10)中：Q为比幅量化层数，Q=64；Δθe为相邻波束最大指向间夹角，即刻进行比幅的角度范围。

2.1.6天线预仰角误差σY

当天线俯仰出现偏移时，天线中心法线指向会出现固定误差σY，如图6所示。该误差在天线全方位方向上具有一致性，即相同距离、相反方向上目标的高度误差相同。

图6 天线预仰角误差示意图

2.1.7天线高度定位仰角误差σC

由于天线转动时各支撑腿受力不均匀、地基沉降等原因，会产生天线的高度定位误差，而引起仰角误差σC，如图7所示。该误差在天线各个方向上是恒定不变的，属于固定偏差。

图7 天线沉降角误差示意图

2.2 方向性误差

2.2.1天线转台水平误差σH

天线转台在调平时往往会存在一定的水平误差，图8给出了天线转台存在水平误差的示意图。

图8 天线转台水平误差示意图

由于存在水平误差σH，这就使得雷达天线在进行机械扫描时，实际扫描线(图8中虚线)与雷达设计扫描线(图8中实线)之间产生σH的偏离，也使得测高仰角在某一方向上为θ-σH，而在相反方向上为θ+σH。通常，转台水平误差的最大值为Vh。实际调平时，由于天线的重力作用，一般在调平方位α处误差最大为vh，而在对称方位α+180°时误差最小为-vh，由于误差较小，在实际计算时可采用下式求得方位β(设α-90≤β≤α+90)上的水平误差为：

(12)

在方位β的对称方位上，水平误差取-σHβ。

2.2.2地形遮蔽误差σZ

三坐标雷达通常采用三波束比幅测高的方法，即通过比较高(3号)、中(2号)、低(1号)3个波束接收到的信号幅度来最终确定仰角。其中2号波束信号最强，当3号波束强度大于1号波束时，采用3号和2号波束进行比幅测高；当3号波束强度小于1号波束强度时，采用1号和2号波束进行比幅测高。当3个波束中出现波束被遮蔽物遮挡或目标回波信号变弱时，就会出现高度突跳的问题。

当目标与雷达之间有遮蔽时，若目标高度位置恰好使得3个接收波束都能接收到回波信号，则测高正常；若1号波束被高山遮挡，则不能收到目标回波信号，只有2号和3号波束能够接收到回波信号，从而使得雷达不能正常的进行比幅测高，此时，雷达测量高度比目标实际高度大；若部分目标回波信号被高山遮挡，而3个接收波束又能接收到信号，则目标回波信号被削弱，此时，雷达测量高度比目标实际高度要低。图9给出了测高时波束与遮蔽的关系。

图9 遮蔽形成测高误差示意图

由于不同方位上遮蔽的情况不同，因此，由遮蔽而引起的测高误差是随方位的遮蔽情况变化的，其误差大小需根据具体遮蔽情况确定。

2.2.3多径效应误差σD

多径效应误差是由于其他物体或表面(如地面、海面等)对目标回波的反射而引起的，这种误差多存在于仰角支路。尤其当目标仰角较低时，不可避免的会产生地面或海面的反射，产生仰角误差。通常，多径效应产生的仰角误差为:

(11)

此外，还有很多因素会形成雷达测高误差，由于这些误差或是对雷达测高误差影响极小，或是属于特殊情况，或是难以测量，如目标闪烁引起的测高误差，由于误差极小可以忽略不计；云雨环境引起的误差，只在云雨天气存在，测量复杂。因此，在这里不再一一阐述。

3 测高误差表征体系构建

3.1 测高误差表征体系

前面区分单向误差和方向性误差2个方面对测高误差的影响因素进行了分析与量化表征，从分析结果可知，不同的误差因素对测高仰角的影响方式不同。从这个角度出发，可以进一步将测高误差划分为直接因素、间接因素和突变因素三类。基于上述因素分析结果，采用德尔菲法进行指标优化与确定，邀请业内8名专家对上述指标进行打分，经过分析比较，对目标闪烁误差、云雨环境误差等指标进行剔除，构建出基于影响方式的误差因素表征体系，如图10所示[14]。

图10 测高误差表征体系框图

直接因素通过直接影响仰角的大小来影响测高精度，其影响具有一定的规律可循，主要包括大气折射误差、天线预仰角误差、天线高度定位误差、转台水平误差等4个二级指标。由于各个因素对测高仰角的影响方式是不相关的，且在某一方向上可以出现仰角数值的叠加，其误差的数学表征为：

σ1=σS+σY+σC+σH

(13)

式(13)中，各类因素计算值的符号表示对仰角增大或减小。

间接因素通过间接影响仰角的大小来影响测高精度，主要包括机内噪声误差、幅度不一致误差、A/D量化误差、角度量化误差、多径效应误差等5个二级指标。这类因素对测高误差的影响具有随机性、不确定性，很难寻找各因素对测高结果的产生具体变化，往往是既有增大高度的时机也有减小高度的时机，而这个时机的随机性很强，难以量化，其数学表征是各因素误差的均方根值：

(14)

突变因素对测高误差的影响往往是伴随遮蔽物的出现而出现的，当遮蔽物对测高产生影响时，雷达高度往往会出现突跳现象，表现为在高度统计数据中出现超出误差范围的数据，称为奇点。突变因素对仰角产生的误差通常由目标、遮蔽物、雷达三者在高度、距离、遮蔽角上的关系确定，也可以根据统计规律获取。

σ3=σz

(15)

三坐标雷达测高误差是通过各类因素综合作用的结果，测高总误差的数学表征为：

σ=σ1+σ2+σ3

(16)

3.2 指标相关性讨论

考虑到指标体系中指标间的交叉和重复性问题，需要进一步对指标的相关性进行分析，为此，基于分离重叠源理论，对指标体系中的指标进行分解，下面进行具体分析。

3.2.1二级指标间独立性分析

构建的指标体系共3个二级指标，即直接因素、间接因素和突变因素。从二级指标对测高仰角误差的作用机理来看，直接因素对测高仰角的作用是由于物理外因作用而产生的，对仰角的影响表现在误差数据叠加上，是与雷达发射信号样式、测高体制等无关的数据指标。间接因素对测高仰角的作用是由于测高体制差异、信号发送接收等作用而产生的，是普遍存在的随机性误差。而突变因素主要是考虑远方遮蔽物对信号的遮挡而产生的高度突变现象，是相对独立性事件。综上，二级指标之间是相互独立的。

3.2.2三级指标间独立性分析

前面分析了二级指标的相关性，下面分析二级指标中子指标(即三级指标)间的相关性。三级指标包括10项指标。直接因素三级子指标中，大气折射误差与雷达站高度和目标高度相关；天线预仰角误差是由于天线俯仰出现了偏移，天线高度定位误差是由于阵地平台沉降等因素产生的，而转台水平误差是由于天线在旋转时由于天线转台的调平误差产生的，各个指标误差的产生机理不同，因此，指标间具有较强的独立性。

对同一部雷达而言，雷达仰角接收波束3 dB波瓣宽度θ3 dB和单脉冲斜率kp是一定的，因此，从给出的误差计算公式看，机内噪声误差主要受脉冲检测信噪比和脉冲数的影响，幅度不一致误差主要受接收机增益比值的影响；A/D量化误差主要受量化位数影响；角度量化误差主要受比幅量化层数和相邻波束最大指向间夹角的影响；多径效应误差主要受主瓣和触地旁瓣增益的比值以及地面反射系数影响。综上，间接因素中各子指标误差产生的主要决定因素不同，因此，各指标间具有较强的独立性。

为了进一步验证各指标间的相关性，采集了7部三坐标雷达的指标数据，运用相关性分析法进行运算，得到各指标间相关系数值如表1所示。

表1 指标间相关系数值

根据相关性分析理论，当|r|≤0.5时，指标为不相关或低度相关[15]。从所得的相关系数的数据来分析，相关系数大于0.5的有3项，其中，多径效应误差与天线预仰角误差的相关系数为-0.53，角度量化误差与天线高度定位误差的相关系数为-0.59，地形遮蔽误差与转台水平误差的相关系数为-0.53。通过对各因素独立性的分析，上述指标之间也具有较强的独立性，因此，建议保留对应指标。

3.3 指标体系优越性分析

与已有的关于测高误差相关研究相比，该误差表征体系主要有3个优势：

1) 分类方法的针对性。该表征体系从测高误差影响因素对测高误差的影响方式出发，将造成雷达测高误差的因素分为直接因素、间接因素和突变因素三类，实现了测高误差因素分离，对于后续开展误差补偿研究而言，该分类方法可以更好的实现误差的针对性补偿，提高雷达测高精度。

2) 表征指标的全面性。当前，对三坐标雷达而言，高度突跳问题是一个普遍存在的测高问题，该表征体系充分考虑了以地形遮蔽为主的突变因素引起的高度突跳，而以往的研究往往没有考虑高度突跳因素，或者把高度突跳问题单独拿来研究而忽略了高度突跳因素外的其他因素对测高误差的影响，相比之下，该误差表征体系考虑更加全面。

3) 测高误差的方向性。以往关于三坐标雷达测高误差影响因素的研究，并没有考虑因素对误差影响的方向性，该误差表征体系在进行因素分析时，将方向性纳入考虑，并区分单向性误差和方向性误差进行了系统分析，可以有效应对不同方向测高误差不同的补偿问题，更贴近雷达测高实际。

4 结论

本文充分考虑误差影响的方向性，区分单向性误差和方向性误差，对三坐标雷达测高误差影响因素进行了系统分析；考虑误差对仰角的影响方式，区分直接因素、间接因素和突变因素等3个方面，构建了三坐标雷达的测高误差因素表征体系，给出了具体的数学表征方式，为进一步研究基于误差分离的测高误差补偿方法，有针对性地对测高误差进行补偿提供了理论支撑。