空间密集目标的群分割算法研究
韩蕾蕾,周 璐
(海军航空大学 研究生大队, 山东 烟台 264001)
弹道导弹等空间目标在中段飞行期间,利用地心引力和最初获得的惯性进行运动,运动特性较为稳定[1]。由于地球近地轨道空间气体密度非常低,空气阻力几乎可以忽略不计,中段运动中释放的各种干扰诱饵,除了与弹头有较小的相对速度外,其初速度全部来源于弹头携带升空后的惯性,各目标之间轨道速度基本相同。相同的轨道速度,较为接近的空间位置,可以作为空间密集群目标进行研究[2]。诱饵释放初期,目标数目以及目标间距会超出传感器的检测跟踪能力范围,传感器并不能目标群中的每个目标,且目标空间分布的密集性易造成目标航迹间的关联错误,这些会引起跟踪的不稳定。为了尽早精确预报空间威胁弹头,就必须通过稳定的跟踪提高数据精度,而且诱饵释放初期离弹道拦截还有相当长的一段时间和距离,此时并不需要精确跟踪到弹头和每个诱饵目标,只需要掌握空间目标群的整体的运动态势即可,即可以对群整体进行跟踪。诱饵与空间弹头间距随着时间推移会逐渐增大,因此要对目标群进行自适应群分割,通过对逐步分裂的子群进行群整体跟踪,来延长稳定跟踪的时间,提高跟踪精度。
由于空间密集目标分群是在目标跟踪步骤之前,因此量测集划分是态势估计的关键步骤,其分群效果直接影响状态估计和滤波算法性能[3-4]。空间目标敌我属性明确,因此群分割主要按照位置关系对空间上目标进行的集合划分。目前,空间目标群分割的主要方法就是距离分割法[5-6]以及其改进后的循环阈值法[7],其都是通过设定距离阈值实现分群,其原理简单易实现,但是空间目标的高密集性容易导致各时刻分割群中成员数量产生波动,从而使分群结果缺乏稳定性。
针对上述问题,本文提出了距离划分与预测划分相结合的联合划分法。算法在航迹起始阶段,通过设定与传感器分辨能力相关的距离阈值,实现无预测信息以及预测信息不可靠条件下的有效分群;在航迹维持过程中,将贝叶斯递推状态和形态进行联合[8-10],将落入某群预测形状波门的所有量测划分为一个群,求取群量测中心并带入群更新的迭代计算中。同时在群量测求取过程中利用概率数据关联[11]的思想代替坐标平均法来获得更为准确的等效群中心。通过联合划分法分群保证了各阶段分群的稳定性,提高群质心的精度,可减少后续关联错误,提高跟踪的准确性。
1 问题描述
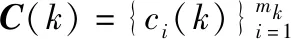
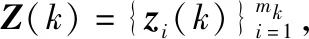

对应k时刻直角坐标系下的量测噪声协方差为

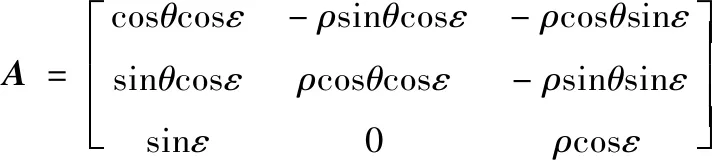
群分割就是对ENU坐标系下的量测集Z(k)及其对应的协方差集R(k)根据一定的准则进行划分。距离划分法中,通过设定与传感器分辨率相关的距离阈值即可实现自适应分群。但由于空间目标具有高密集性,即使已经分裂开的两个子群也很容易由于其边缘某些量测的相近性而被划分为一个群来进行跟踪,这样相近的测量时刻中各目标群会反复分裂与合并,进而使群状态估计产生较大的误差。因此文中考虑只在无预测信息或者预测信息不可靠的航迹初始阶段考虑采用距离划分方法进行群分割,在航迹起始成功后,考虑通过形状波门对下一时刻的量测进行聚类,其划分结果与当前时刻的预测群中心以及预测形状矩阵相关,即使在目标量测比较近时,也能将量测划分给不同的群中心,从而避免两个群的合并,得到误差相对较小的状态和形状估计。
2 距离划分法


(1)
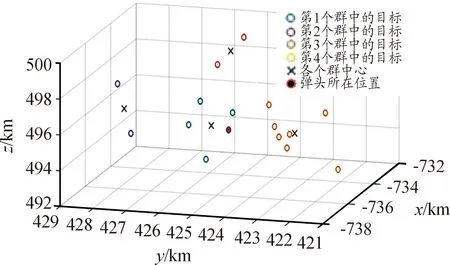
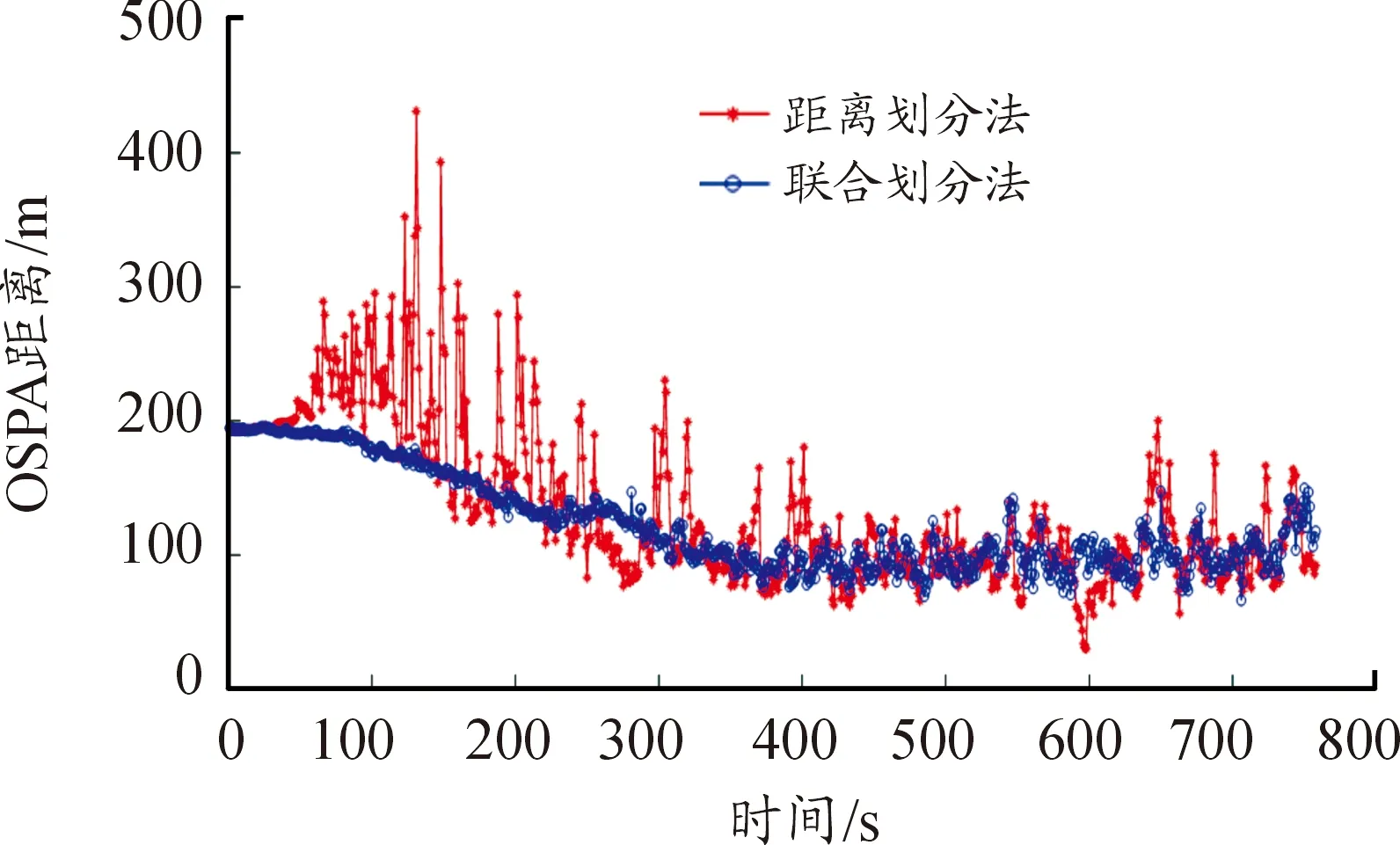
若d(zi(k),zj(k)) 利用式(1)计算Z(k)中任意两个量测之间的距离并与d0比较,可最终将Z(k)分割成多个不同的群。设Z(k)最终可分为m个群,记为{U1,U2,…,Um},且 定义两个不同的群Ui和Uj之间的距离为 1≤m≤ni, 1≤n≤nj 当d(Ui,Uj)≥d0,Ui和Uj为分离的两个群;当d(Ui,Uj) 1≤m≤ni,1≤n≤ni,m≠n (2) (3) 距离划分法一般任意选取一量测为种子量测划分波门,将落入波门内的全部量测划分给该群,归类完毕后再在剩余量测中选择另一个种子量测,以此类推进行分类,同时还要判断两个群间的距离是否满足合并条件;循环逻辑法则是以落入波门内的每一个量测为中心重新建立波门,寻找落入新波门内的量测。两种算法都具有一定的逻辑复杂性,文中给出了另一种相对简单的逻辑思路,即将满足距离阈值条件的量测对全部筛选出,然后统一进行合并划分,其算法具体实现如下: 1) 求量测间距离。根据公式求取当前时刻k所有量测间距离并存储,可得到mk(mk-1)/2个量测间距离。 2) 预分割群。找到所有距离元素的最小值,若该最小值小于距离阈值d0,则把该距离对应的位置坐标及量测编号i,j进行存储,同时将该最小距离赋值为无穷大,让其不参与下次最小值的竞争,重复上述步骤,直至最小值大于阈值,至此筛选出所有满足阈值要求的预分割群u1,u2,…,ul,各个群之间有大量重复元素,后续步骤主要通过量测编号判断是否进行群的合并及单目标群的划分。 3) 进行群的合并。若两个量测群中有重复元素,则进行合并运算得到一个群,重复步骤,直到所有群之间没有重复元素为止,至此得到n个群U1,U2,…,Un。 4) 划分单目标群。在完成上述步骤后,若判断量测集Z(k) 中还有剩余量测并不属于划分的任何一个目标群,则该量测单独分为一个群,得到单目标群Un + 1,Un + 2,…,Um,至此量测集Z(k)最终分割为m个群,记为{U1,U2,…,Um}。 5) 求取群中心数据。根据式(2)和式(3)进行群中心坐标和对应协方差的求取。 为更准确描述空间目标运动状态,考虑用空间动力学方程进行约束,因此某质心运动状态的动态模型可描述为 x(k+1)=F(k)x(k)+D(k)gr(k)+ω(k) 其中状态转移矩阵F(k)=F1(k)⊗Ιd; ⊗为克罗内克积运算符号,Ιd∈Rd×d为单位阵。d为空间维数,这里d=3。 式中:α为机动时间常数的倒数;T为采样间隔。 gr(k)为当前时刻的重力加速度,D(k)=D1(k)⊗Ιd,且 ω(k)为ENU直角坐标系下零均值的高斯过程噪声,且 ω(k)~N(0,Q(k)⊗Xk) 而 Xk为d×d维对称正定的随机矩阵,过程噪声的协方差矩阵Q(k)⊗Xk表明,质心运动状态的不确定性取决于目标扩展形态(包括大小、形状和朝向),目标的形态越大,其质心形态的不确定性也越大。 其中:aM为机动加速度的极大值;pM为机动加速度等于极大值的概率;p0为机动加速度等于0的概率。 针对某群目标,运动状态的一步预测为 协方差的一步预测 P(k+1|k)=F(k)P(k|k)F′(k)+Q(k) 量测值的进一步预测 其中 新息 新息协方差 S(k+1)=H(k+1)P(k+1|k)H′(k+1)+R(k+1) 增益 K(k+1)=P(k+1|k)H′(k+1)S-1(k+1) 状态更新方程 与扩展目标类似,空间群目标的形态可以用对称正定的随机矩阵表征[12-14],设k时刻某群目标的椭球方程为 式中:变量y(k)代表椭球表面上的点;H(k)x(k)为群的质心位置;X(k)为正定矩阵,其特征值为椭球中3个轴的长度,方向为椭球3个轴的方向。 形状一步预测为 形状更新为 X(k+1|k+1)=X(k+1|k)+N(k+1)+ 其中 N(k+1)=S-1(k+1)V(k+1)V′(k+1) B(k+1)为形态观测矩阵,且 nk+1为落入该群波门的量测个数。 最初3个时刻的群中心为基于距离划分得到的群中心,后续预测过程中群中心是根据落入波门内的量测获得的。 形状预测波门为 新一时刻传感器探测后,判断选出落入各群波门内的所有量测,由于各群之间距离依旧比较近,各波门之间有交叉重叠,同一个量测可能落入多个群波门中,因此可借鉴概率数据关联的思想来求取各等效群中心,其关键步骤是得到波门内每一个量测来自预测群中心的后验概率,可用量测j与群中心t的高斯似然函数[15]求得: 其中,νjt(k+1)为落入群中心t波门内所有量测与群中心t之间的组合新息;S(k+1)为对应的组合新息协方差。 为了进一步预防相邻群间的合并,考虑对接近预测位置的量测做重加权,即对互联概率基于距离关系进行二次加权。 群中心t与量测j间概率的二次加权值为 其中,m为k+1时刻落入群中心t候选波门的量测个数;rtj为航迹t与量测j间的欧式距离。 量测j与群中心t互联概率为 δjt=βjt*wjt 此时得到的航迹t与所有候选量测间的概率之和并不等于1,需要做归一化处理,最终量测j与群中心t互联概率φjt,其中 对于未关联上的群目标数据,采用距离划分法进行群分割,并按照3/3逻辑法进行航迹起始判别,即有连续3个时刻的群等效中心满足航迹起始判断条件,即判定该航迹起始成功。对于一个新目标群,设其出现的最初时刻为时刻1,后续相应为时刻2、3。同时将各时刻中所有的群赋予相应的群编号。 1) 建立1-2可能航迹。求取时刻1和时刻2两个量测i、j之间的距离,若量测间的距离在初始波门内,则判断初始关联成功形成1-2可能航迹,遍历所有量测间距离,若存在一组量测满足波门要求,可能航迹的个数加1,最终得到m条可能航迹,其航迹的编号是根据存储时间的前后自动进行编号的,其中初始波门大小为 其中:KG为波门常数;T为采样间隔;vi为第i个群目标1时刻的最大可能速度。 在所有关联判断结束时,若第1时刻某个群目标的初始波门内无对应的第2时刻的关联数据,则可认为该群目标第2时刻漏检,该群目标航迹起始失败;若还有多余的第2时刻数据未关联上,则将第2时刻该数据作为新出现的群目标第1时刻的数据,重新赋予相应的群编号,然后和后续时刻的数据进行关联判断。 2) 判断是否形成1-2-3确认航迹。若1-2可能航迹的个数m为0,则所有航迹起始失败,否则对可能航迹进一步判断能否形成1-2-3确认航迹。针对所有可能航迹,根据其时刻1,2的测量位置进行直线外推,得到时刻3的预测点,并根据式(4)求取时刻3所有的预测点与所有的测量点之间的统计距离。将预测点位置、1-2时刻量测点的编号和对应距离作为一个关联对存储在数组中。 (4) 将所有距离进行排序,选取其中的最小距离,若Dmin≤γ,则其对应的1-2可能航迹与时刻3测量点关联成功,确认航迹数量增加并将其对应的1,2,3量测进行存储,然后删除与已关联的预测点和时刻1、2量测点相关的所有关联对的数据。对剩余距离重复上述步骤直至最小距离大于阈值,至此获得所有的1-2-3确认航迹。 对于已经航迹起始成功且未终止的航迹,即可以按照状态估计算法对群中心和形状波门进行预测,然后以预测群中心为中心作形状波门,完成后续量测针对各群的归类划分,并将等效群中心测量直接分配给产生波门的群航迹,完成后续群更新迭代计算。设置航迹外推点个数上限M,在外推点个数小于M时,若航迹关联失败,用预测值作为更新值进行航迹的维持,一旦外推点个数达到上限要求,则群航迹终止。 对于预测划分完后并未被聚类到任何群中的量测,继续采用距离划分的方法进行群分类,直至将所有量测归类完毕。下一时刻将重新对未起始成功的群中心进行航迹起始判断,若航迹起始成功,则加入航迹预测与更新过程中。综上,基于联合划分的群跟踪流程如图1所示。 图1 联合划分法跟踪流程框图 设传感器采样间隔为T=1 s,观测时间为0~760 s,传感器测距误差均方差为6 m,方位和俯仰测角误差均方差均为0.001 4 rad,空间目标x、y、z三轴上的初始速度均为3 000 m/s,设置15个诱饵伴随空间目标飞行,诱饵释放时刻为初始时刻,诱饵相对弹头的释放速度在3~10 m/s按均匀分布随机选择。采用考虑地球椭球形状的标准椭球地球重力模型,其对应ENU坐标系下的目标加速度模型为 其中,x、y、z为ENU坐标系下的目标位置;μ为万有引力常数;re为地球赤道半径;J2为地球二阶带谐系数,而 设B为雷达站大地纬度,φ为雷达站地心纬度,令θ=B-φ,ρ=re+z,则 而 其中ω为地球自转角速度。 仿真生成了雷达对空间密集目标的测量数据,其ENU坐标系下三轴位置图如图2(a)所示,图2(b)、(c)、(d)分别给出第701~710 s间x、y、z三轴位置随时间的变化图,并用16条不同颜色线表示16个目标轨迹。图3为选取的第100个测量时刻时空间目标在ENU坐标系下的位置分布情况,其中各个颜色代表各目标的分群情况,可见此时空间密集目标共被分为4个群,其中弹头与距离较近的诱饵被划分到同一个群中。 图2 密集群目标的量测位置曲线 图3 第100 s时的空间目标位置分布情况 为了验证本章所提算法的有效性,将文中提出的联合划分法与单独使用距离划分法后的目标跟踪结果进行对比分析。图4是两种划分方法下滤波器估计的目标数目,可见在两种算法下的空间密集目标均是由一个群逐渐分裂成多个目标群,。距离划分法各个时刻分群数目波动较大,这主要是由于目标间距离非常近,从而出现了前后时刻群分割后的各个群中包含的目标数量会发生微小变化,而联合划分法中一旦航迹起始成功,将根据预测进行群划分,群分割结果相对比较稳定。随着时间的延长,目标群逐步分裂成传感器能够识别和跟踪的多个空间目标,此时目标数目为弹头和诱饵的总数目。 图4 两种算法下分群数目 为了进一步验证两种群分割方法对跟踪结果的影响,采用OSPA距离对估计误差进行分析,图5显示的是两种划分算法下滤波器估计的OSPA距离。可见在最初的一段跟踪时间内两种算法下跟踪的OSPA误差相差不大,这是由于此时目标均被划分为一个群,但是随着群的逐渐分裂,联合划分法下的OSPA距离误差略小于距离划分法下的误差,在跟踪的精度上体现出一定的优势。而且文中算法下误差的波动也比较小,这是由于距离划分法中各个群中的目标数量波动导致等效的群中心位置产生波动,因此跟踪过程中产生较大的估计误差,而联合划分法群分割结果相对比较稳定,避免了估计误差的波动。在各个目标已经完全分离开的后续跟踪阶段中,两种算法的分群都非常稳定,误差精度就基本相同了。图6显示的是两种划分方法下的单步运行时间,可见文中算法在提高精度的同时整体上具有较好的实时性。 图5 两种算法下OSPA距离 图6 两种算法下单步运行时间 针对空间密集目标分群问题,提出了距离划分与预测划分相结合的联合划分算法,保证了各阶段分群的稳定性,同时提高了群质心的精度及跟踪的实时性,有利于后期传感器对目标的精确预报,具有工程应用价值。后续工作可进一步研究更为准确的形态估计模型进一步提高分群的稳定性与精确性,同时使算法更加适应复杂的空间作战环境。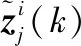


3 形状预测划分法

3.1 目标的状态估计

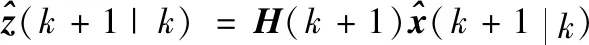
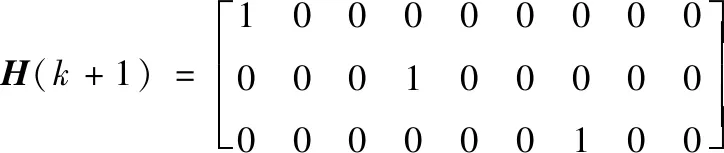

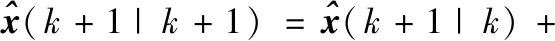
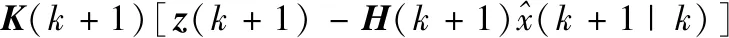
3.2 目标的形态估计



3.3 群中心数据的获取
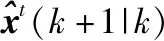

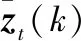
4 群航迹起始与维持
4.1 群航迹起始


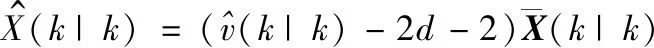
4.2 群航迹维持

5 仿真分析

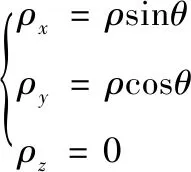




6 结论

