成对旋转不变的共生自适应完全局部三值模式

陈晓文，刘光帅，刘望华，李旭瑞

西南交通大学 机械工程学院，成都610031

纹理作为图像的重要底层特征之一，在图像的分类与识别中有着重要的作用，且被广泛应用于图像处理、计算机视觉等领域中，因此，纹理的研究有着重要的现实意义[1]。常用的纹理特征提取方法有灰度共生矩阵方法[2]、马尔可夫随机场方法[3]、小波变换方法[4]、分形理论[5]等。但是，以上几种方法计算复杂度较大，且对光照变化、噪声干扰等问题较为敏感，从而影响图像的分类效果。

为了降低纹理特征提取的计算成本，提高图像的分类精度，让图像分类技术更有效地应用到实际工程中，一些学者开始研究更加快速、稳健的纹理特征提取算法。局部二值模式（LBP）最早由Ojala等人[6]提出，由于其原理简单、计算复杂度低的特点被广泛运用到工业检测、场景分类、人脸识别、医学图像分析等领域。然而，原始的LBP 算法对图像旋转、尺度、非均匀光照变化鲁棒性较差，学者们相继提出LBP改进算法。其中，Liu等人[7]对近年来LBP改进算法做出了详细的总结与对比，分析了各种算法的优劣性。Tan 等人[8]提出的LTP 算法通过引入量化阈值对邻域像素进行正负编码，提高了算法对光照变化和噪声的鲁棒性。Guo等人[9]提出的完全局部二进制模式（CLBP）算法，通过提取局部纹理结构的中心像素信息（CLBP_C）、中心像素值与其邻域像素的差分符号信息（CLBP_S）和幅度信息（CLBP_M）这三种信息增强了算法的鉴别能力和对光照变化的鲁棒性。文献[10-11]提出的完全局部三值模式（CLTP）算法则是上述提到的LTP与CLBP算法的结合改进，将量化阈值引入到CLBP算法中，从而使改进后的算法鉴别能力更强，且增强了算法对噪声和光照变化的鲁棒性。Liu 等人[12]提出的扩展局部二值模式（ELBP）主要提取的是局部邻域像素灰度特征和径向灰度差分特征，在光照和旋转变化的纹理分类中有较好的效果；随后Liu等人[13]为了增强算法对噪声的鲁棒性提出了中值抗噪的扩展局部二值模式（MRELBP），其是在ELBP 的基础上用局部邻域块的中值代替中心像素的灰度值，具有较好的抗噪能力，同时多尺度的密集采样增强了算法的分类性能。以上几种方法主要集中在单个纹理特征的提取，多个特征间的共生往往能够描述更复杂的局部纹理结构。Qi等人[14]提出的PRICoLBP算法，通过联合编码空间上下文共生特征可以描述更复杂的纹理结构和高阶特征信息，然而PRICoLBP算法选取的空间点对之间的梯度方向会随图像旋转而发生变化，因此算法对图像旋转变化较为敏感。高攀等人[15]对PRICoLBP算法做出了相应改进，提出了EPRICoELBP 算法，其利用像素点LBP 特征极值对应的邻域起始编码点与局部中心像素点来确定方向矢量选取空间上下文共生点，增强算法对旋转变化的鲁棒性，但其存在的问题是没有对算法的抗噪性进行进一步研究，算法对噪声的鲁棒性较差。

综上，本文提出一种增强成对旋转不变的共生自适应完全局部三值模式。算法的内容包括：（1）利用LTP算法对邻域像素进行正负编码得到两个局部二值模式（Upper 模式和Lower 模式），在两个模式中分别利用像素点LBP 特征极值对应的邻域起始编码点与局部中心像素点来确定方向矢量选取空间上下文共生点，减少噪声对共生点对选取的干扰；（2）利用CLTP算法分别提取两个模式共生点的局部纹理特征；（3）在原始的LTP、CLTP 算法的基础上，将固定的量化阈值优化为适应各个图像纹理特征的自适应阈值。

本文算法的贡献和优点主要有：（1）通过引入LTP改善了原始PRICoLBP 和EPRICoELBP 算法对噪声较为敏感的缺点，增强了算法对噪声的鲁棒性；（2）更多的共生点能够提取更加丰富的纹理特征，提升了算法的鉴别性能；（3）自适应阈值代替原始固定阈值，使算法适用于各类图像，能够更好地适应环境和光照变化。

1 局部二值模式及相关改进算法

1.1 局部二值模式（LBP）

局部二值模式是一种简单、典型的纹理分类特征提取算法，如图1 所示，它将中心像素的每个邻域点灰度值以该邻域中心的灰度值为阈值进行二值量化，当邻域点灰度值大于或等于中心灰度值时编码为1，小于则编码为0，以此形成一个二进制模式，然后将该二进制模式以x正半轴方向为起点逆时针旋转串联得到一个二进制串，最后将该二进制串转换为十进制数作为该像素点的LBP特征值。LBP的数学表达为：

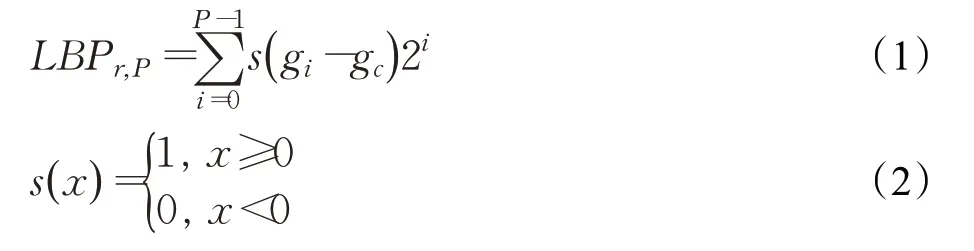
其中，r表示邻域半径，P表示半径为r的圆形邻域上采样点的个数（图1中，P为8），gc表示局部邻域中心点的灰度值，gi(i=0,1,…,P-1）表示邻域点的灰度值。

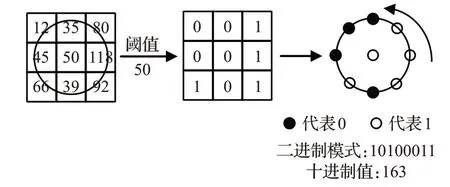
图1 原始LBP算子计算示例

然而，当图像旋转变化时，某中心像素的圆形邻域像素也会发生变化，从而引起LBP特征值的变化。为了使LBP 具有旋转不变性，Ojala 等人[16]提出了一种旋转不变的算子LBPrir,p，即不断变化圆形邻域的起始编码序列，得到一系列LBP 特征值，选取其中的最小值作为该邻域的LBP特征值，其数学描述为：

其中，ROR( )a,i表示将a对应的二进制数循环右移i位。在引入旋转不变模式后，LBP算法对有旋转纹理变化图像的分类有了更稳定的识别率。

但随着邻域点数P的增加，算法的特征维度呈指数型上涨。为了满足LBP 算法的时效性，Ojala 等人[16]在旋转不变模式的基础上，提出了LBP旋转不变均匀模式（riu2）和旋转不变的非均匀模式，具体定义为：

其中，U值表示LBP 模式中圆周上相邻两个元值1/0（或0/1）的变换次数，当U值小于等于2时，旋转不变均匀模式被归为P+1 类，所有的旋转不变的非均匀模式被归为一类，最后用于表示整幅图像纹理的LBPriu2r,p直方图矢量特征仅为P+2 维，有效地降低了特征维度，使得运算速度取得了较大幅度地提升，因此，LBPriu2r,p被研究者广泛应用。

1.2 局部三值模式（LTP）

LTP算子是对LBP算子的扩展，它将邻域像素灰度值gi和中心像素灰度值gc的差值与阈值t做比较，当差值大于等于t时，则该邻域点像素值量化为1；当差值在[-t，t]之间，则该邻域点像素值量化为0；当差值小于等于-t时，则该邻域点像素值量化为-1。其数学表达式如下：

其中，P，r，gc，gi已在式（1）中定义过，t代表LTP的阈值。

由于阈值t的引入，使得LTP 的抗噪性比LBP 要好。为了简化算法的计算，Tan等人将局部三值模式进一步分解为正值计算部分和负值计算部分，将除1以外的值标记为0后得到的编码，定义为Upper模式；将除-1以外的值标记为0并用1取代原来的-1得到的编码，定义为Lower模式，如图2所示。由此可见，LTP分解成了两个局部二值模式。

1.3 成对旋转不变的共生局部二值模式（PRICoLBP）

文献[17-18]表明特征间的空间共生能够提高算法对纹理特征的识别能力，因此，多种特征间的相关共生往往能够描述比单个特征更大、更复杂的局部纹理结构。Qi 等人[14]提出了一种成对旋转不变的共生局部二值模式，其通过计算图中任意像素点A的梯度方向和法向方向来确定两个共生点B1和B2，再根据A点的局部信息编码B1、B2点的特征，最后，利用(A,B1)、(A,B2)两个点对共同描述A点处较大范围内的局部纹理信息，同时，(A,B1)和(A,B2)两个点对之间的夹角能够描述高阶的局部特征信息，因此，PRICoLBP 算法在处理图像分类时具有较好的识别能力，其数学描述如下：

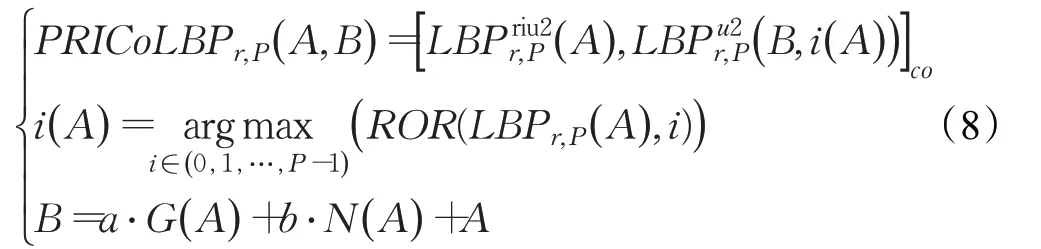
其中，(A) 表示A点的局部纹理特征，i(A) 表示A点最大LBP 特征值对应的邻域起始编码点序号，(B,i(A) )表示共生点B以第i(A) 个邻域点为编码起始点对应的局部纹理特征，G(A) 、N(A) 分别表示像素点A的单位梯度方向和单位法向方向，a、b表示共生点对间的空间尺度模板，分别为（a，0）和（0，b）。

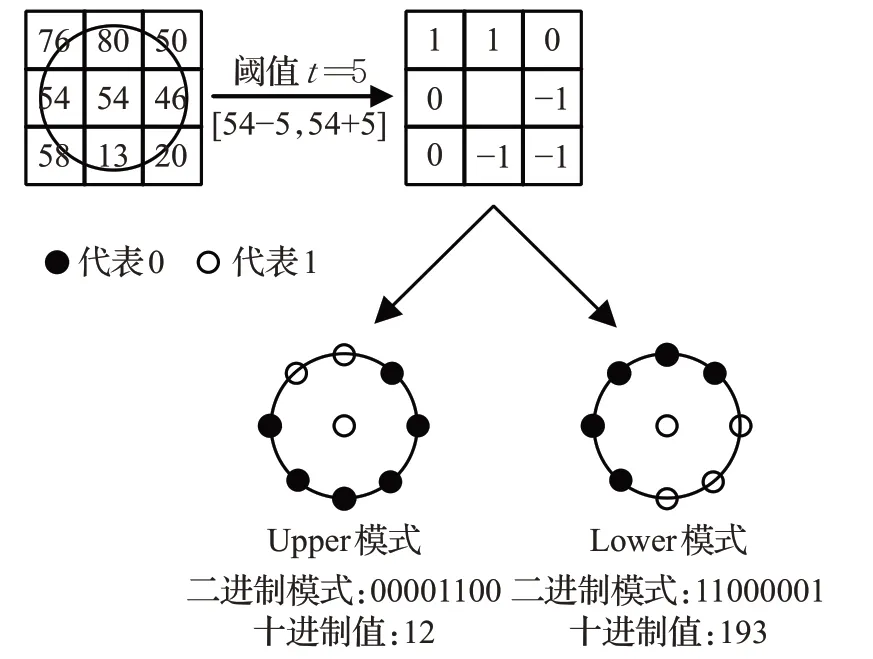
图2 LTP算子计算示例

以上三种算法虽然广泛运用于纹理特征提取中，但优缺点也很明显。其中，LBP 算法计算维度较低，运算速度快，但对纹理特征的描述较少，且对噪声敏感；LTP算法因为引入了阈值t使算法对噪声具有一定的鲁棒性，但依然不能较好地描述纹理特征；PRICoLBP 算法通过两点共生使算法能够提取更复杂的纹理结构，增强了算法的鉴别能力，但其对噪声干扰、旋转变化较敏感。

2 增强成对旋转不变的共生自适应完全局部三值模式

原始的PRICoLBP 算法选取的上下文共生点对之间的梯度方向会随图像的旋转发生变化，因此对图像的旋转变化较敏感，文献[15]对PRICoLBP 算法做出了改进，其利用像素点LBP特征极值对应的邻域起始编码点与局部中心像素点来确定方向矢量选取共生点，增强了算法对图像旋转变化的鲁棒性，但存在受噪声影响较大的缺点，轻微的噪声干扰可能会影响共生点对的选取，从而影响分类精度。针对以上问题，本文提出了一种对图像旋转、光照变化、噪声干扰鲁棒性较强的算法，记为增强成对旋转不变的共生自适应完全局部三值模式。

2.1 具有抗噪性的共生点对选取

为了减少噪声干扰对选取共生点的影响，本文引入LTP 算法将共生点的计算过程分为两个模式，即Upper模式和Lower 模式。LTP 算法在抗噪性方面要优于普通的LBP 算法[8]，由于设置了阈值区间，能够减少计算结果受像素灰度差异变化带来的影响，因此，在计算共生点的位置时受噪声影响较小，增强了算法对噪声的鲁棒性。如图3 所示，在LTP 两个模式中，分别以像素点A1、A2（由于在两个模式中A 点邻域编码不同，这里分为A1、A2点）和其LBP 特征极值对应的邻域编码起始点确定两个方向矢量m、n，通过这两个方向矢量来确定和像素点A1、A2共生的四个点B1、B2、C1、C2，更多的共生点对能够提取到更多的局部纹理信息，增强了算法的分类性能。同时，从图3 中看出，A1、A2点的LBP特征极值对应的邻域起始编码点具有旋转不变性，因此，由LBP特征极值确定的上下文共生点的相对位置信息和高阶夹角特征并不会随图像旋转而改变，从而有效地增强了算法对图像旋转变化的鲁棒性。图4～6 给出了本文共生点对的选取方法与文献[15]中方法在噪声干扰下的对比。

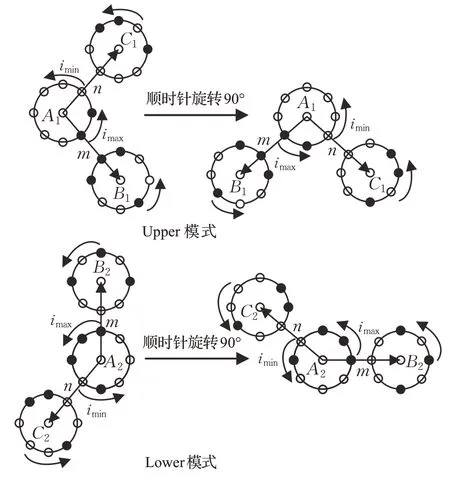
图3 改进算法的旋转不变示意图

图4 左侧是TC10 纹理库中的一张普通图像，右侧表示在这张图像中添加了高斯噪声，然后分别提取这两张图像相同位置处大小为3×3的局部邻域，由于噪声的干扰局部邻域发生了较大的变化；图5 表示文献[15]的共生点选取方法，左图为处理普通图像所选取的共生点，右图为处理噪声图像所选取的共生点，可以看出，因为噪声的干扰导致像素点LBP 特征极值对应的邻域起始编码点发生了改变，共生点的位置也因此发生改变；图6表示本文的共生点对选取方法，因为设置了容忍区间[-t，t]（此处t取5），本文方法选取的共生点对的位置并没有因为噪声干扰的影响而发生改变。因此，本文算法通过引入LTP能够减少噪声对共生点对选取的影响，从而使算法对噪声具有一定的鲁棒性，同时由两点共生变为四点共生，能够提取到更丰富的局部纹理信息。

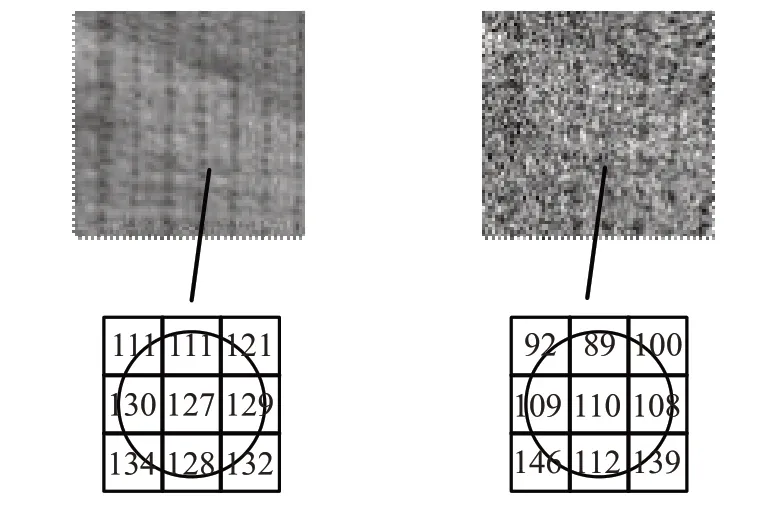
图4 普通图像（左）和添加了高斯噪声的图像（右）

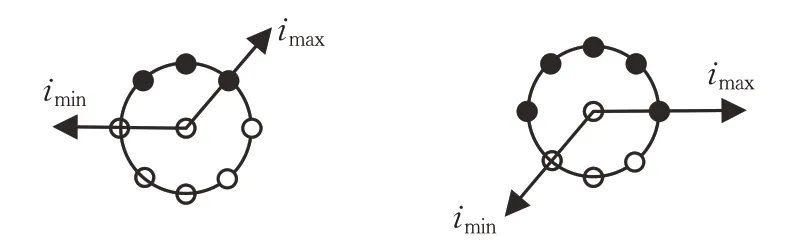
图5 文献[15]选取共生点对的方法

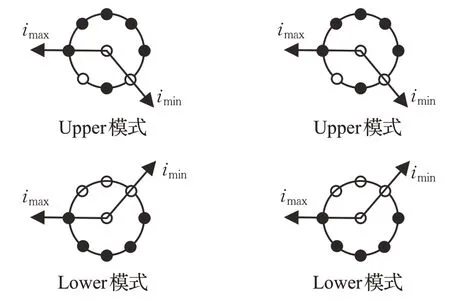
图6 本文选取共生点对的方法

2.2 融合CLTP的局部纹理特征

考虑到LBP 算子对纹理信息提取不足等问题，文献[10-11]提出了一种CLTP 算法，CLTP 是CLBP 与LTP算法的结合。文献[10]表明，CLTP 具有比CLBP 和LTP更强的纹理特征描述能力和抗噪能力，因此，本文用CLTP 算法能够提取更丰富的局部纹理特征，且对噪声有较好的鲁棒性。CLTP与CLBP一样被分为了三部分（CLTP_S、CLTP_M、CLTP_C），同时由于LTP 的引入每个部分也会有两个模式（Upper 模式和Lower 模式），因此，分别使用CLTPUpper和CLTPLower算法提取两个模式共生点的局部纹理特征。

CLTP_S 即为原始的LTP，也是将邻域像素灰度值gi和中心像素灰度值gc的差值与阈值t做比较，其数学描述如下：

其中，gc、gi、t已在式（7）定义过，这里不再阐述。

CLTP_M主要提取像素值的差值幅度信息，其数学描述如下：

其中，|gi-(gc+t)|，|gi-(gc-t)|，cupper和clower则分别为两个模式中全部与的均值。

CLTP_C 则是提取图像的中心像素信息，其数学描述如下：

其中，u已在式（14）中定义过，cI为整幅图像的平均灰度值，=gc-t。

为了提取更为充分、准确的局部纹理信息，使算法对噪声有较强的鲁棒性，本文提取上下文共生点A、B、C的CLTP 特征，在Upper 模式中的A1、B1、C1点采用CLTPUpper进行编码；在Lower 模式中的A2、B2、C2点采用CLTPLower来编码。编码时采用旋转不变均匀描述子（riu2）。其数学描述可表示为：

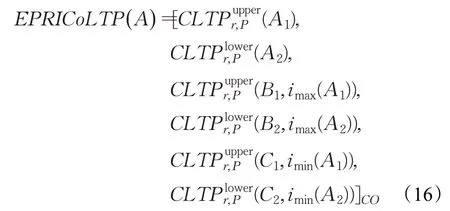
其中，imax(A) 、imin(A) 分别表示A点最大LBP 特征值和最小LBP特征值对应的邻域起始编码点序号。

2.3 自适应阈值

由于传统的LTP算子的阈值t一般为定值，单一的阈值无法适应不同纹理的图像，且噪声图像不同区域的噪声强度有所差别，因此固定阈值的LTP算子的抗噪性并不强。根据定义知LTP将邻域像素灰度值gi和中心像素灰度值gc的差值与阈值t进行比较，因此本文将局部邻域的各像素点和中心像素点的标准偏差作为自适应阈值，局部标准偏差反应了中心像素点与局部邻域像素点的离散程度，能够降低图像受噪声干扰的影响，其具体计算如下所示。

（1）计算中心像素与邻域像素点的差值Δgi：

其中，P与式（1）中P的含义相同，表示邻域采样点个数。

本文通过引入自适应阈值算法，使阈值t根据图像的局部纹理进行自适应选取，从而对光照变化和噪声干扰有了更好的鲁棒性，使图像的每个区域都有其相适应的动态阈值，并且将自适应阈值T用于上述所使用的LTP和CLTP当中。

2.4 本文算法的计算流程

本文算法的具体流程如下：

（1）提取图像的LTP特征，得到Upper和Lower两个模式。

（2）分别计算两个模式中A1、A2点极大、极小值对应的邻域起始编码点序号，并设定中心像素点与共生点对的距离为4，找出A1的共生点B1、C1，A2的共生点B2、C2。

（3）使用CLTP 算法提取A1、A2、B1、B2、C1、C2点的局部纹理特征。对于Upper模式的A1、B1、C1点使用CLTPUpper编码；对于Lower 模式的A2、B2、C2点使用CLTPLower编码。将得到的特征结果联合生成直方图（LTP和CLTP均采用自适应阈值t）。

（4）将得到的直方图送入支持向量机（SVM）进行纹理分类训练。本文算法的流程图如图7所示。

3 实验和分析

3.1 实验参数选择及数据库选取

为了验证本文算法对光照多样性和图像旋转变化的鲁棒性，本文选取标准纹理库Brodatz、Outex（TC10、TC12-h、TC12-t、TC14）、CUReT、KTH_TIPS，UIUC进行实验，在这些纹理库中用LBP、LTP、CLBP、MRELBP 和PRICoLBP及文献[15]中改进算法EPRICoELBP与本文算法进行对比，同时，在存在光照、旋转、尺度变化的KTH_TIPS 纹理库中添加不同强度的高斯噪声和椒盐噪声，来进一步验证算法对噪声干扰的抵抗能力。为了确保实验对比的公平性，本文算法和所有的LBP及其改进算法均采用旋转不变均匀模式，邻域采样点数为8，MRELBP 的邻域半径根据文献[13]设置为2、4、6、8，其余算法的邻域半径设置为2，LTP 算法的阈值t设定为5。然后利用卡方核支持向量机（SVM）来评估各类算法的分类性能，SVM的惩罚因子c选取默认值1。为了避免误差，在每个纹理库进行分类实验时采用100次独立随机采样的平均分类值作为评估算法性能的指标。实验中所用的数据库的纹理特征和训练集样本数如表1 所示。Brodatz 和KTH_TIPS 部分纹理样本如图8、9所示。

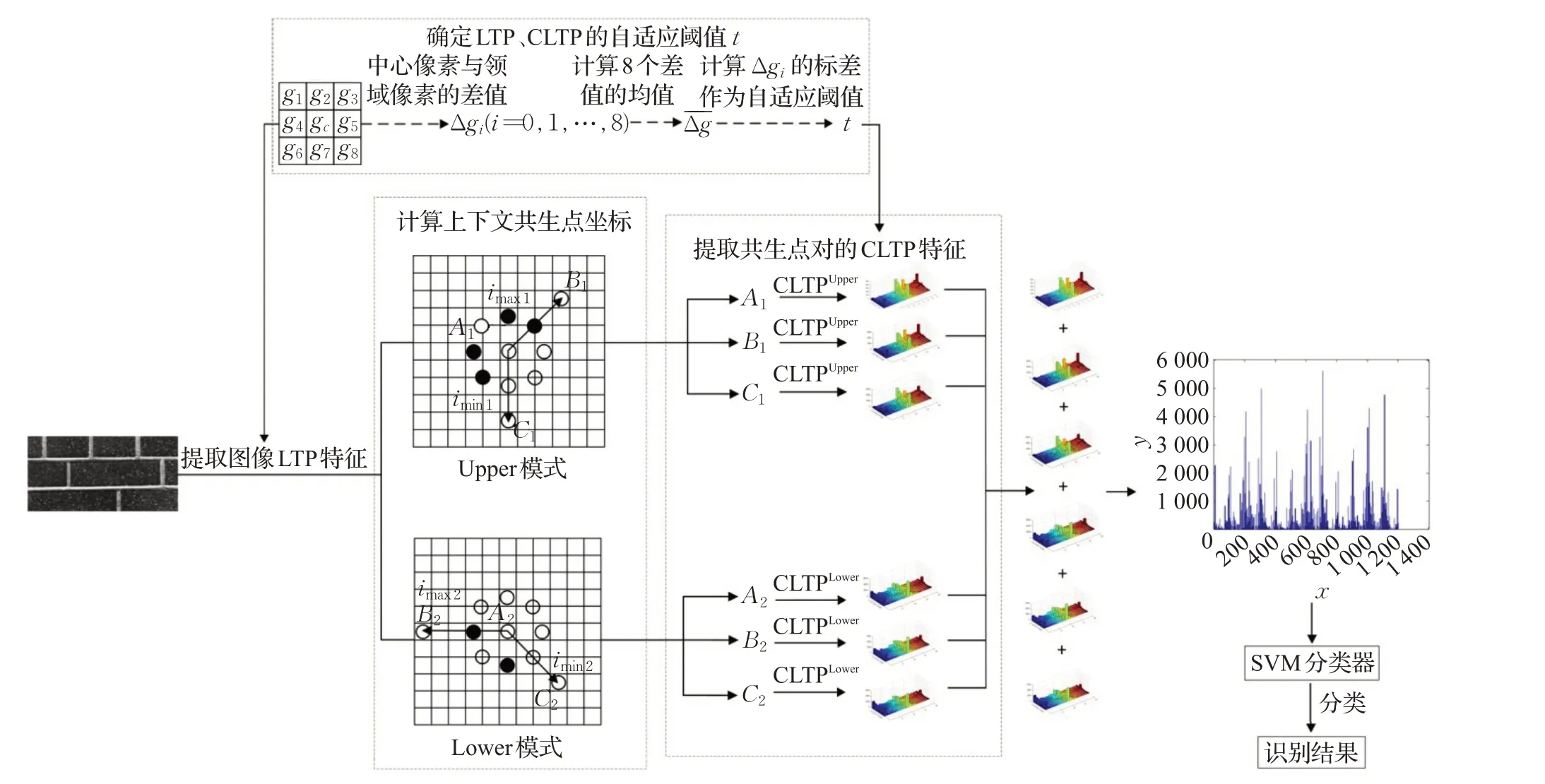
图7 算法流程图

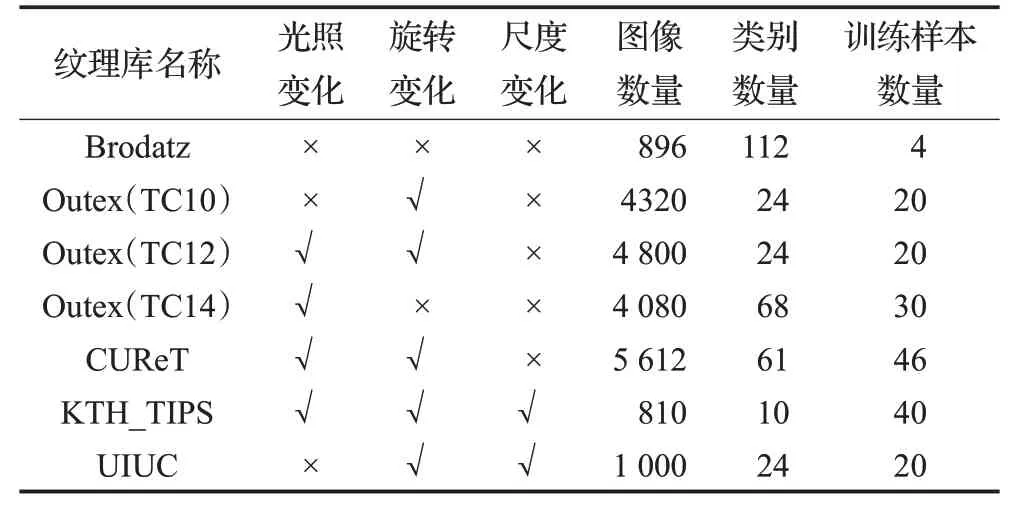
表1 实验中所用纹理库的特征

图8 Brodatz部分纹理样本

图9 KTH_TIPS部分纹理样本

3.2 实验结果和分析

3.2.1 无噪声环境下的分类结果

由表2 知：对于相同光照、视角和尺寸不变的Brodatz纹理库分类，本文算法的识别率均高于其他LBP算法，这说明本文算法有较强的特征鉴别能力；对于仅存在光照变化的TC14 纹理库，本文算法均明显高于其他LBP算法，说明本文算法通过引入自适应阈值t能够较大地提升算法对光照的鲁棒性，减轻外界环境变化对图像分类带来的影响；对于存在视角、尺度变化的UIUC纹理库，本文算法识别率比原始的PRICoLBP 提升了5.01%，这说明本文算法利用像素点LBP特征极值对应的邻域起始编码点与邻域中心像素点确定方向矢量来选取空间上下文共生点，能够有效地增强算法对图像旋转的鲁棒性；KTH_TIPS纹理库不仅存在剧烈的光照变化，还存在旋转和尺度的变化，本文算法在KTH_TIPS纹理库的识别率比PRICoLBP、EPRICoELBP、MRELBP算法分别提高了1.83%、0.71%、1.04%，这表明本文算法通过融合多个上下文共生点的局部CLTP特征，对光照、旋转、尺度变化有较强的鲁棒性，有效增强了算法的鉴别能力。在TC12、TC10、CUReT纹理库中，本文算法相对于各类LBP算法依旧取得了较高的识别率，进一步验证了本文算法对光照变化和图像旋转变化有较强的鲁棒性。

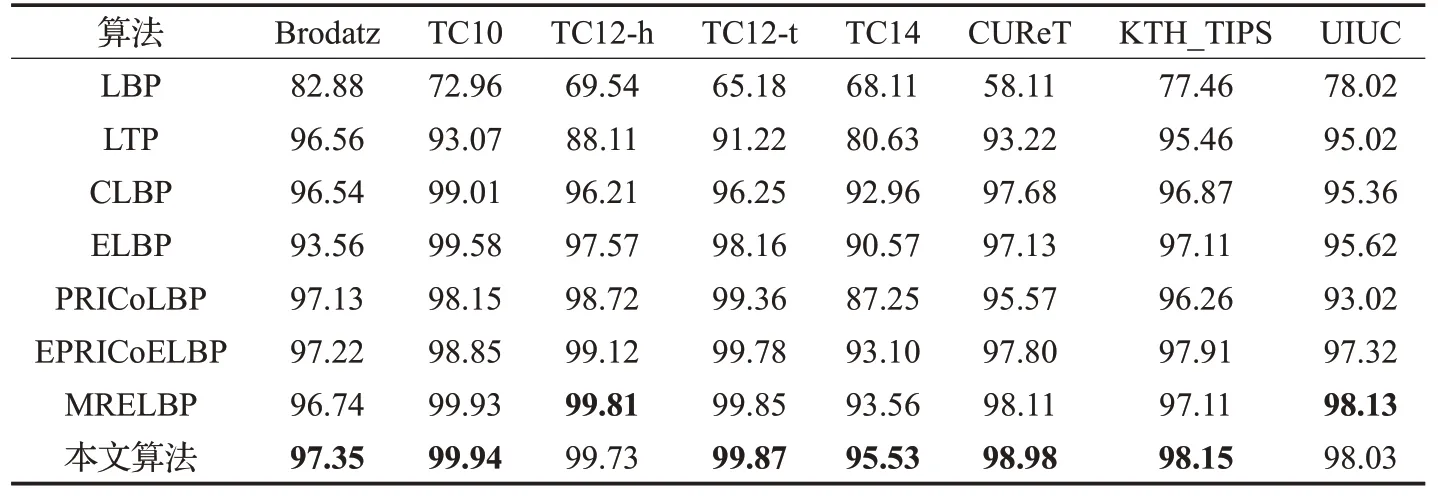
表2 不同算法在各纹理库上分类识别率对比 %

3.2.2 有噪声环境下的分类结果

为了验证本文算法对噪声的鲁棒性，选取PRICoLBP、EPRICoELBP、LTP和抗噪性能较好的MRELBP算法与本文算法进行对比。图10 和图11 分别是在KTH_TIPS纹理库中测试不同算法对椒盐噪声和高斯噪声的鲁棒性。其中，椒盐噪声的密度用ρ表示，数值设置为0.1、0.2、0.3、0.4、0.5；高斯噪声的方差用ν表示，数值设置为0.01、0.02、0.03、0.04、0.05。由图知：随着图像噪声强度的增加，PRICoLBP 和其改进算法EPRICoELBP 的识别率较低，而本文算法依旧保持着较高的识别率，这说明利用LTP 两个模式中像素点的特征极值来确定上下文共生点，减少了噪声干扰对选取共生点的影响。在添加椒盐噪声的纹理分类实验中，本文算法的识别率要高于除MRELBP 外的算法，MRELBP 算法由于对图像进行了中值滤波处理，中值滤波在处理椒盐噪声的图像时效果较好，因此MRELBP 算法对椒盐噪声的鲁棒性要更强；在添加高斯噪声的纹理分类实验中，本文算法均高于其余算法，这表明本文算法对高斯噪声有较强的鲁棒性。综上所述，通过引入自适应阈值t并应用到LTP和CLTP中能够使算法具有较强的抗噪能力。

3.2.3 特征维度和特征提取时间对比

表3 给出了不同算法在KTH_TIPS 纹理库中特征维度和特征提取时间的对比情况，特征提取时间表示提取一张图片的纹理特征所消耗的时间。从表中数据知，本文算法相比于原始的PRICoLBP算法特征维度仅仅提高了20 维，但在分类性能上有了明显的提升。EPRICoELBP 算法虽然仅有600 维，但该算法在计算时使用了多尺度梯度幅值加权，成倍增加了特征提取时间，本文算法不仅提高了计算效率，且增强了算法对噪声的鲁棒性。

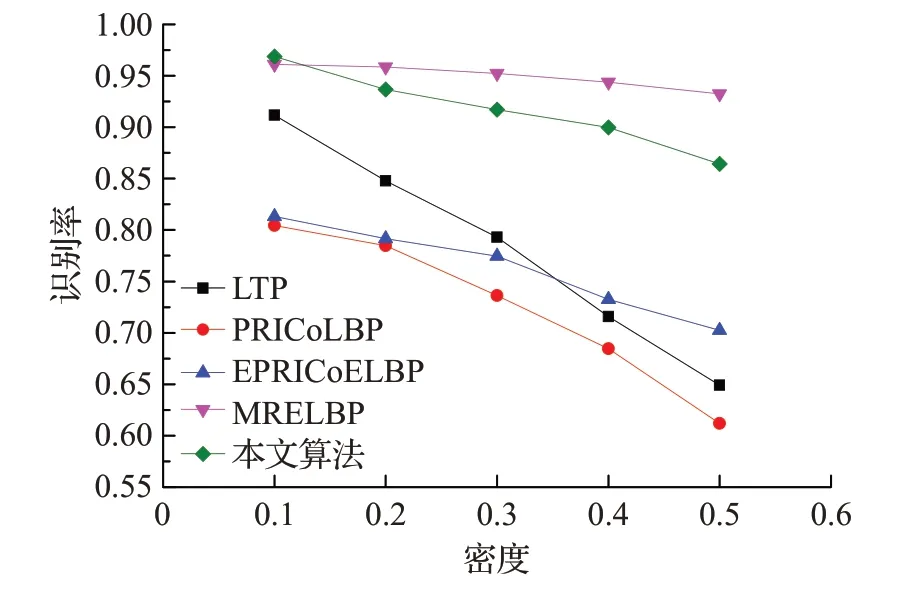
图10 不同算法在不同强度椒盐噪声分类识别率对比

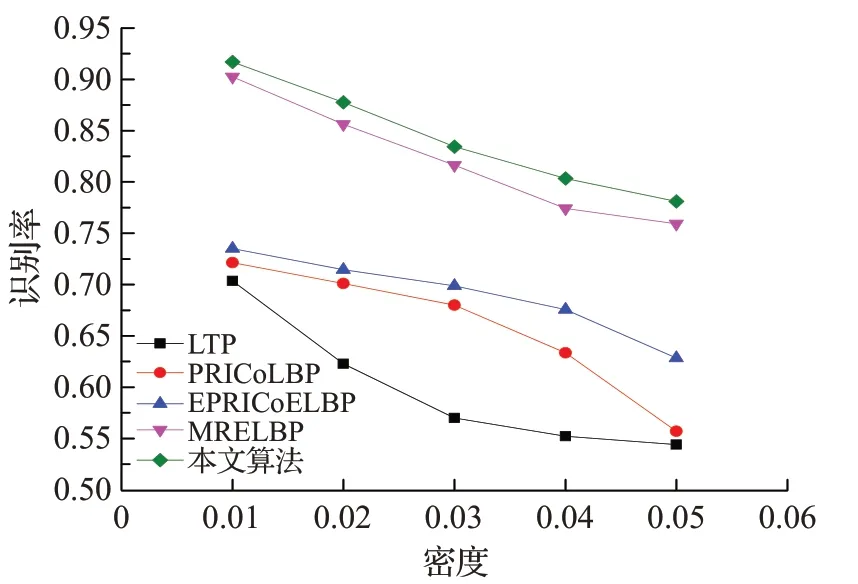
图11 不同算法在不同强度高斯噪声分类识别率对比

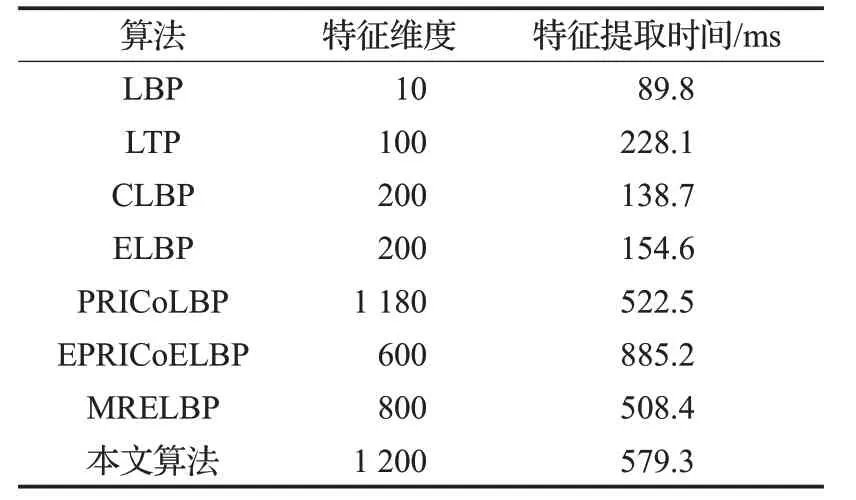
表3 不同算法在KTH_TIPS纹理库上计算复杂度

4 结论

本文提出了一种增强成对旋转不变的共生自适应完全局部三值模式，其主要针对原始的PRICoLBP对图像旋转、光照变化鲁棒性较差和改进算法EPRICoELBP对噪声较为敏感的问题进行改进。通过在无噪声和有噪声的纹理库上的分类实验表明，本文算法相比于其他算法取得了较好的识别结果。本文算法通过利用LTP两个模式中像素点的特征极值来确定上下文共生点，使算法具有旋转不变性，且减少了噪声干扰对选取共生点的影响，然后用CLTP算法提取更丰富、有效的共生局部纹理特征，同时，引入自适应阈值t应用到LTP和CLTP中，使算法能够根据图像自身的纹理特征确定阈值，具有较强的抗噪性和适应性。

由于本文所用的数据库均为灰度纹理图像，缺乏对彩色图像的讨论。因此，下一步的研究方向，是将图像的颜色信息融入到本文算法中，围绕算法对彩色图像的分类展开研究。