生鲜电商配送的开放式时变车辆路径问题研究

付朝晖，刘长石

1.长沙民政职业技术学院 软件学院，长沙410004

2.湖南工商大学 工商管理学院，长沙410205

生鲜电商已经成为我国农产品上行的主要渠道之一，根据中商产业研究院的数据，2019年我国生鲜电商行业的市场交易规模约为3 225 亿元，较上年同期增长49.4%，大有可为。但是，由于生鲜农产品具有易腐易损性，生鲜电商客户具有单次购买量小、购买频次高且具有服务时间窗等特点，使得生鲜电商的物流配送成本高昂。物流配送已成为生鲜农产品“最后一公里”的关键环节，解决生鲜电商的配送问题，有利于提高生鲜电商核心竞争力，促进生鲜农产品销售、农民增收与农村发展。

解决生鲜电商配送问题的关键是科学规划配送车辆的行驶路线，即求解生鲜农产品配送的车辆路径问题（Vehicle Routing Problem，VRP）。由于生鲜农产品主要采用普通车辆配送，大部分学者研究常温条件下生鲜农产品配送的VRP。文献[1]针对新鲜蔬菜配送问题，以总配送成本最小为目标构建带时间窗车辆路径问题（Vehicle Routing Problem with Time Windows，VRPTW）优化模型，设计一种启发式算法求解。文献[2]针对生鲜农产品市场需求的时变性与模糊不确定性特点，构建生鲜农产品“多供应点选择”与“最早分发”为优化目标的VRP模型。文献[3]针对生鲜农产品配送时效性强的特点引入生鲜农产品生鲜度损耗系数，以总配送成本最小和顾客满意度最大为目标建立多目标VRP模型。文献[4]考虑B2C 环境下顾客需求特点，以总配送成本最小和顾客满意度最大为目标构建VRP 模型。以上文献具有一定参考价值。经过长期的生鲜农产品物流实践，业界与学者们认为冷链物流能有效提高生鲜农产品配送质量。文献[5]根据生鲜农产品冷链配送特性，以总成本最小为目标构建生鲜农产品冷链配送的VRPTW模型，设计改进遗传算法求解。文献[6]以生鲜农产品冷链物流的网点建设成本和运营成本为优化目标构建非线性混合整数规划模型。文献[7]以生产者收益最大为目标建立冷链配送的VRPTW 模型。文献[8]根据生鲜品运输的时效性设计相应的时间窗及惩罚成本，构建冷链环境下以车辆运输成本、派遣成本以及时间惩罚成本和生鲜损耗成本之和最小为目标的VRP模型。文献[9]考虑到生鲜农产品需求的高鲜活度、多品种与小批量特性，以配送成本最小为目标建立冷链环境下生鲜农产品多隔室的VRP模型。这些研究能为生鲜农产品冷链配送提供方法参考。考虑到客户对生鲜农产品有新鲜度要求，学者们研究新鲜度限制条件下生鲜农产品配送的VRP。文献[10]研究不同配送环境、不同时间窗要求以及不同产品变质系数条件下生鲜农产品的新鲜度与配送成本。文献[11]综合考虑企业运营成本和顾客对产品新鲜度要求，以总配送成本最小、交付产品的新鲜度最大为目标，建立具有最低新鲜度限制的易腐品生产-配送协同调度双目标优化模型，设计非支配排序遗传算法求解。以上研究成果可为提高生鲜农产品配送的客户满意度提供理论支撑。由于生鲜电商的客户主要分布在城市，城市路网具有时变特性，部分学者研究生鲜电商配送的时变车辆路径问题（Time-Dependent Vehicle Routing Problem，TDVRP）。文献[12]研究车辆灵活出发时间条件下生鲜农产品配送的TDVRP。文献[13]优化实时路况信息条件下生鲜农产品的配送路径。文献[14]综合考虑路况、时间窗与生鲜损耗等因素构建生鲜农产品配送的多目标VRP 模型。文献[15]基于经济成本与环境成本兼顾的视角，研究生鲜电商配送的TDVRP。以上研究比较符合生鲜电商配送的实际情况，具有一定借鉴价值。

已有文献为深入研究生鲜农产品配送问题提供良好基础，但仍存如下缺口：（1）已有成果大多研究生鲜农产品配送的封闭式VRP。然而，由于资金不足或者仅注重核心业务等原因，许多中小型生鲜电商都把配送业务外包给第三方物流企业。这种情况下，配送车辆在生鲜电商的仓库装货后开始服务，完成任务后不必回到生鲜电商的仓库，即开放式车辆路径问题（Open Vehicle Routing Problem，OVRP）。但是，关于生鲜电商配送的OVRP 研究文献较少。（2）已有文献大都设定车辆在同一时间从仓库出发。实际上，为保障生鲜农产品送达客户时的鲜活度，配送车辆应该根据实际情况在不同时间从仓库出发。（3）生鲜电商的客户主要分布在城市，城市路网具有时变特性。然而，同时考虑城市路网的时变特性、生鲜农产品送达客户时的新鲜度限制、客户需求量与时间窗等因素的研究成果不多。（4）已有研究大多根据行驶距离计算车辆使用成本，但在时变路网环境下，行驶距离最短并不一定对应行驶时间最短，有可能导致较高的人力成本与车辆油耗成本，使得总配送成本不是最低。本文针对以上研究缺口，研究鲜活度限制条件下生鲜电商配送的开放式时变车辆路径问题（Open Time-Dependent Vehicle Routing Problem，OTDVRP）数学模型与求解算法，以期为生鲜电商提供物流配送的方法借鉴与决策参考。

1 问题描述

某生鲜电商将配送业务外包给一个第三方物流企业，有多个客户需要配送，各客户地理位置与时间窗已知，需求量都小于车辆容量，有且只能有一辆车服务一次。为明确本文适用范围，做出如下假设：（1）车辆可以根据需要在不同时间从生鲜电商的仓库出发，完成任务后不必回到该仓库。（2）车辆可以提前到达客户位置，但必须等待至该客户的最早开始服务时间才能配送。（3）生鲜农产品送达客户时具有最低鲜活度限制。（4）交通路网具有时变特性，车辆在不同时间段内的行驶速度不同。（5）车辆有固定使用成本，根据车辆使用时间（包括车辆行驶时间、等待时间与服务时间）产生相应的人力成本。决策问题：第三方物流企业如何合理规划配送车辆路径，使得总配送成本最少？

2 数学模型

2.1 跨时间段的路段行驶时间计算

由于早晚交通高峰、交通管制与意外事故等原因，城市路网的交通状况具有时变特性，车辆在不同时间段内以不同速度行驶。时变路网条件下，车辆可能需要跨越多个时间段才能行驶完某一路段，车辆行驶时间难以直接计算，需要合理处理[16]。

文献[17-18]采用“先进先出”准则设计时变路网条件下的车辆行驶时间计算方法。本文借鉴已有方法，将全天24 个小时平均划分为多个时间段，设定不同时间段内的车辆行驶速度不同。

令Z为时间段的固定时间长度；T={T0,T1,…,TL}为时间段集合；[Th-1,Th]为第h个时间段；Shijk为时间段h内车辆k在路段(i,j)上的行驶速度。不同时间段内的车辆行驶速度如图1所示。

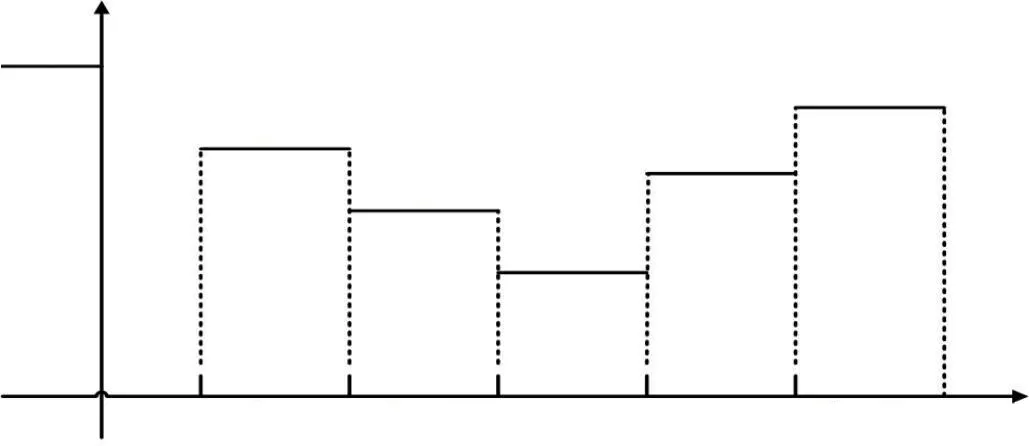
图1 车辆在各时间段内的行驶速度

令为时间段h内车辆k在路段(i,j)上的行驶时间；lik为车辆k从节点i的出发时间，lik∈[Th-1,Th]；ajk为车辆k到达节点j的时间。依据图2，各时间段内车辆k在路段(i,j)上的行驶时间分为3种情况：（1）出发时间段内的车辆行驶时间为Th-lik。（2）中间时间段内的车辆行驶时间为Z。（3）最后时间段内的车辆行驶时间为ajk-Th+β。

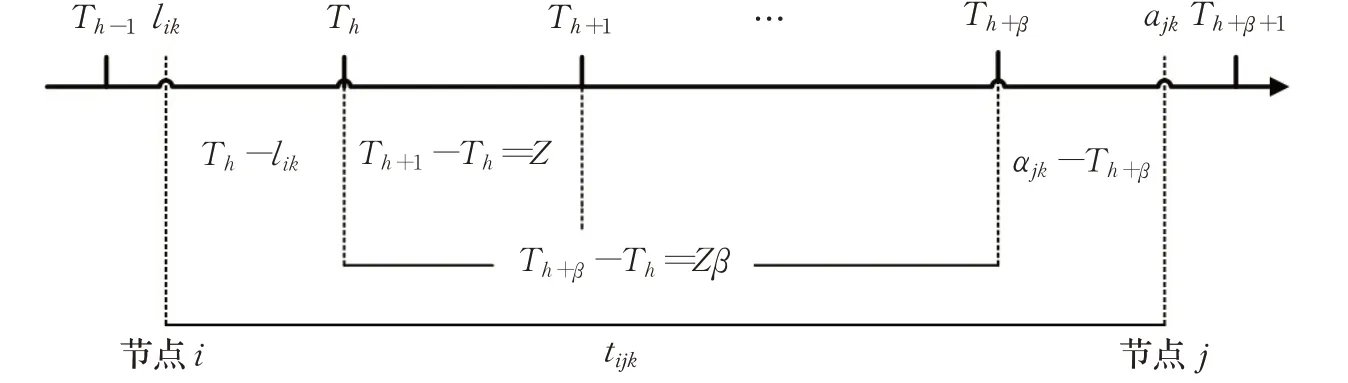
图2 车辆在各时间段内的行驶时间

令Lij为路段(i,j)上的距离；为时间段h内车辆k在路段(i,j)上的行驶距离，为在时间段h后车辆k行驶完路段(i,j)全程还需要行驶的距离；tijk为车辆k行驶完路段(i,j)全程的行驶时间。跨时间段的路段行驶时间计算方法步骤如下：

步骤1 出发时间段内的车辆行驶时间计算。=(Th-lik)，如果≥Lij，tijk=，路段行驶时间计算完毕；否则，=Lij-=Th-lik，转步骤2。

2.2 生鲜农产品的鲜活度度量

文献[3]定义生鲜农产品随时间变化的新鲜度损耗计算方法。文献[11]给出常温条件下农产品运达客户时的鲜活度度量方法。考虑到本文设定生鲜电商通常采用普通车辆配送货物，采用文献[11]的生鲜农产品鲜活度度量函数：

其中，tik表示生鲜农产品经由车辆k送达客户i的时间，1 为生鲜农产品从仓库运出时的鲜活度，Tb为生鲜农产品的最大保质时间，tik≤Tb。

2.3 数学模型

2.3.1 符号与变量

符号：C为客户集合；N为物流网络内的所有集合，N=C⋃0，0 表示仓库，i,j∈N；di为客户i的需求量；V为车辆集合；Q为车辆容量；c1为车辆使用的固定成本；c2为车辆使用的单位时间成本；B为生鲜农产品送达客户时的最低鲜活度；[bi,ei]为客户i的服务时间窗；si为客户i的服务时间；wik为车辆k提前驶达客户i的等待时间，如果aik ＜bi，wik=bi-aik，否则wik=0。

变量：vk如果车辆k被启用，值为1，否则为0；xijk如果车辆k从节点i行驶到节点j，值为1，否则为0；如果车辆k在时间段h内行驶在路段(i,j) 上，值为1，否则为0；zik如果客户i由车辆k服务，值为1，否则为0。

2.3.2 OTDVRP数学模型

以总配送成本最小为目标，构建鲜活度限制条件下生鲜电商配送的OTDVRP数学模型如下：

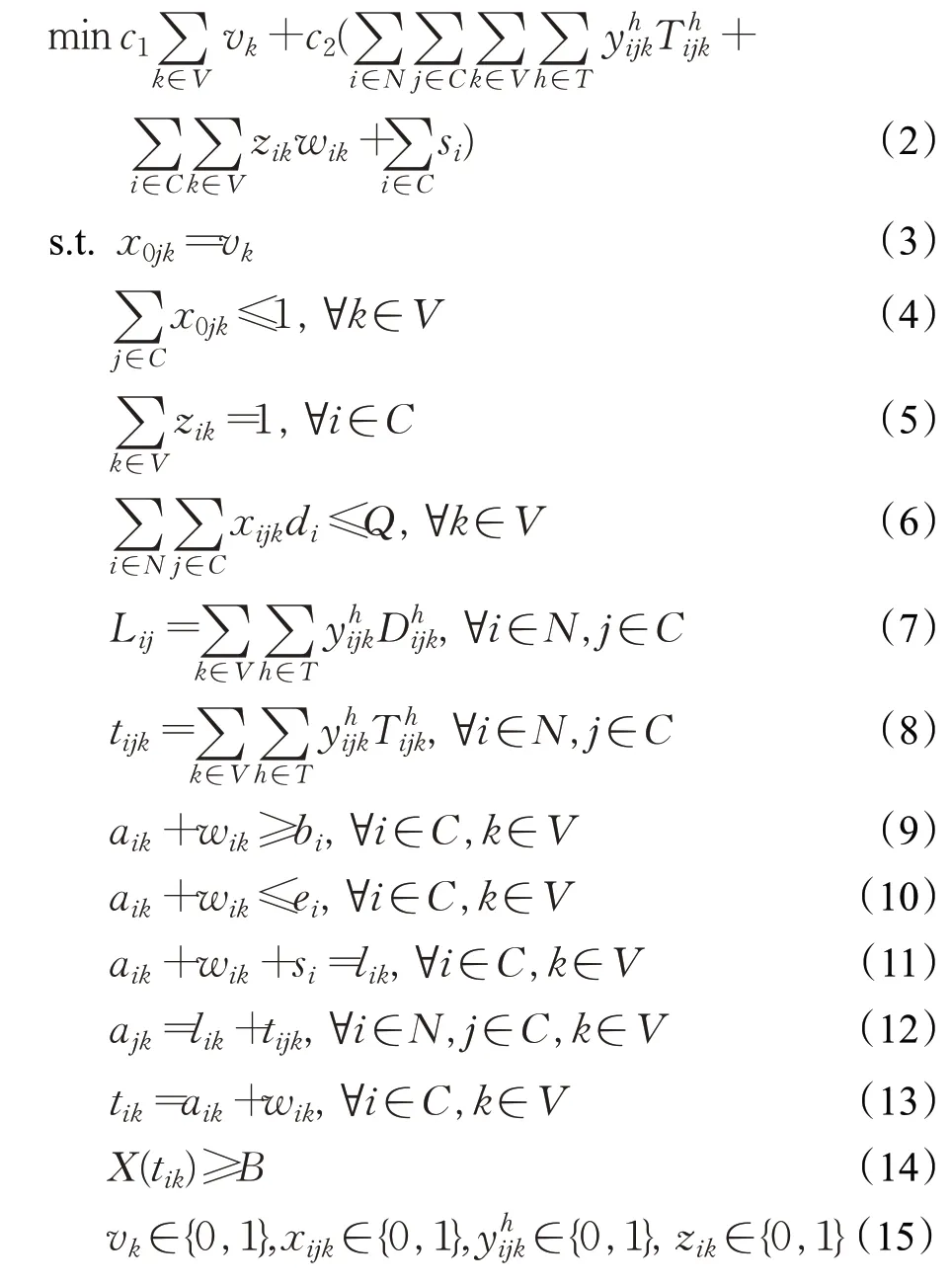
式（2）为目标函数，表示最小化车辆使用的固定成本与车辆使用时间（包括车辆行驶时间、等待时间与服务时间）产生的人力成本之和。约束式（3）表示如果车辆被启用，必须从仓库出发。约束式（4）表示每辆车最多启用一次。约束式（5）表示每个客户能且只能被一辆车服务一次。约束式（6）表示车辆装载量不能超过容量限制。约束式（7）表示路段距离与车辆在各时间段内行驶距离之间的关系。约束式（8）表示车辆关于某路段的行驶时间与车辆在各时间段内行驶时间之间的关系。约束式（9）与（10）表示客户服务必须在时间窗内进行。约束式（11）表示车辆到达客户时间、等待时间、服务时间与离开客户时间之间的关系。约束式（12）表示车辆从上一个节点行驶到下一个节点之间的时间计算方法。约束式（13）表示车辆为客户配送货物的具体时间计算方法。约束式（14）表示生鲜农产品送达客户时必须满足最低鲜活度。约束式（15）表示变量的取值约束。

3 求解算法设计

VRP 属于NP-hard 问题，难以求得最优解，通常采用启发式算法求得满意解。OTDVRP比普通VRP更加复杂，求解将更加困难。蚁群算法是一种启发式全局优化算法，具有启发式搜索、分布计算与信息正反馈等优势，已经成功应用在VRP、指派问题、Job-shop 调度、网络路由问题等方面[19-20]。本文根据OTDVRP模型特性，设计一种改进蚁群算法（Improved Ant Colony Algorithm，IACA），思路如下：（1）为优先配送时间窗较窄的客户，在转移规则里面引入时间窗宽度启发式因子；（2）为避免蚁群算法过早陷入局部最优、增强蚁群算法搜索的全局性，引入自适应信息素启发式因子和期望启发式因子。

IACA的具体步骤如下：

步骤1 初始化。初始化程序的所有参数与变量，令maxiter表示程序最大迭代次数，iter表示当前迭代次数，mincost为最优成本，loadk为车辆当前装载量，M为蚂蚁数量，iter=1，mincost=+∞。

步骤2 构建可行解。（1）将所有蚂蚁都放在仓库，令m=1。（2）依次派出蚂蚁m，令k=1。（3）令loadmk表示蚂蚁m当前使用的车辆k的货物装载量，loadmk=Q。（4）计算蚂蚁m的车辆k从当前节点i行驶到节点j的转移概率pij：

其中，τij为信息度浓度启发式因子；ηij为能见度启发式因子，ηij=1/Lij；φij为节点j的时间窗宽度启发式因子，φij=1/(ej-bj)；α、δ与ϑ分别表示信息素启发式因子、期望启发式因子与时间窗宽度启发因子的重要性，allowedm表示蚂蚁m的所有未访问节点集合。（5）找出转移概率pij值最大的节点jb，采用公式（6）计算节点jb是否满足车辆容量限制，采用跨时间段的路段行驶时间计算方法与公式（8）计算车辆k从节点i行驶到节点jb的行驶时间tijbk，采用公式（13）计算农产品由车辆k送达客户的时间tjbk，采用公式（1）计算生鲜农产品送达客户的鲜活度X(tjbk)，如果满足车辆装载量、客户时间窗、生鲜农产品送达客户时的最低鲜活度等限制，车辆k从节点i行驶到节点jb，loadmk=loadmk-djb，jb∉allowed；否则，k=k+1，重新从仓库派出车辆服务，转（3）。（6）如果蚂蚁m还有节点未访问，转（4）。（7）如果所有蚂蚁访问完毕，转步骤3，否则，m=m+1，转（2）。

步骤3 当前迭代的结果计算。（1）计算当前迭代的最优总成本costiter，如果costiter ＜mincost，mincost=costiter。（2）计算每辆车的出发时间、车辆使用时间、行驶距离，iter=iter+1。

步骤4 自适应信息素启发式因子和期望启发式因子设计。参考文献[20-21]的方法，令α=1+3(iter/maxiter)，δ=3-2(iter/maxiter)。

步骤5 信息素更新。更新当前迭代最优路径的组成路段信息素，即：

其中，ρ为信息素挥发性，0 ≤ρ ＜1；Δτm ij为蚂蚁m在路段(i,j)上信息素增加量；F为常数；fm表示蚂蚁m的总配送成本。

步骤6 算法结束条件。如果iter≤maxiter，转步骤2，否则算法结束。

4 算例分析

4.1 实验设置

由于目前没有生鲜农产品配送的标准数据库，同时也考虑到生鲜电商客户分布的多样性，采用VRPTW数据库[22]的C 类型、R 类型与RC 类型算例为本文测试算例。C 类型、R 类型与RC 类型算例的客户坐标分别属于集中分布、随机分布与混合分布。各算例有1个仓库与100个客户，第一行数据为仓库坐标，其余100行数据是客户坐标、需求量与时间窗。另外，为满足测试需要，补充如下数据：（1）设定仓库的工作时间为早上7：00。（2）设定每个客户的服务时间为5 min，各时间段的时间长度为10 min。（3）将8：00至9：00、18：00至19：00设为交通拥堵时间段，车辆行驶速度设定为20 km/h。（4）非交通拥堵时间段内的车辆行驶速度设定如下：令4种车速分别为[55,40,65,30]，根据时间段h采用求余函数Y=mod(h,4)，当Y取值为1、2、3 与0 时分别对应4 种车速。

参考文献[17，19]的方法，将算法参数设置如下：c1=200元/辆，c2=0.3元/min，Q=1 000单位，maxiter=600，M=30，ρ=0.15 ，ϑ=3、F=20，Tb=780 min、B=0.7。算法采用Matlab R2016a 编程，在Intel®Core ™ i5-8250U CPU @1.60 GHz 1.80 GHz，RAM 8.00 GB的微机上运行。

4.2 实验结果

4.2.1 多类型算例的开放式车辆路径规划分析

为检验本文IACA 算法的可行性与有效性，采用C类型、R 类型与RC 类型多种客户分布的多个算例进行实验。计算结果如表1 所示。表中，IN 表示算例名称，TC表示总配送成本（单位：元），VUT表示车辆总使用时间（单位：min），VTD 表示车辆总行驶距离（单位：km），VN 表示车辆使用数量（单位：辆），RT 表示算法运行时间（单位：s）。

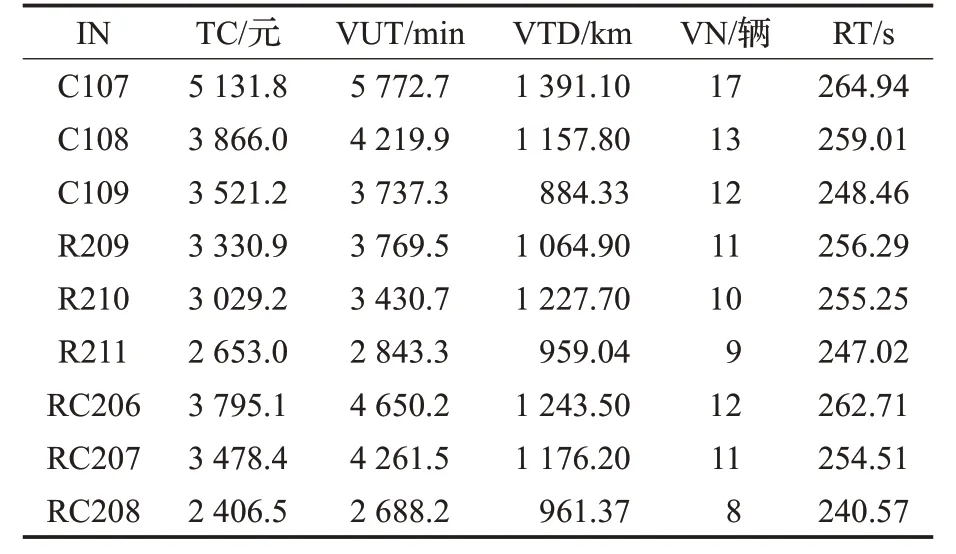
表1 不同类型算例的计算结果

根据表1 的数据可以得出如下结论：（1）根据TC、VUT 与VN 的计算结果可知，相对于R 类型与RC 类型的算例来说，C 类型算例的总配送费用相对较高，车辆使用时间较长，车辆使用数量较多。主要原因在于C类型算例属于集中分布，每个客户都与仓库的距离较远（参见图3（a）算例C109 的配送路径规划），车辆行驶到第一个客户时需要较长的时间，从而影响该车辆运载的生鲜农产品送达后续客户时的鲜活度；而R 类型与RC类型算例的客户分布相对均匀，车辆配送路线是由近至远，每辆车先配送离仓库近的客户，再配送离该客户较近的客户，缩短车辆驶达客户时间，有效提高生鲜农产品送达客户时的鲜活度（参见图3（b）算例R209 与图3（c）算例RC206的配送路径规划）。（2）根据VTD与VN的结果可知，同一类型的算例中，车辆总行驶距离越长，车辆使用数量越多。（3）算法的最大运行时间为264.94 s，最小运行时间为240.57 s，说明本文算法能够在较短时间内求解不同客户分布类型的算例，给出决策者满意解，具有可行性与有效性。

算例C109、R209 与RC206 的配送路径规划如图3所示。图3中的黑色菱形代表仓库，米字形黑点代表客户，实线代表车辆行驶路径。从图3可知，C类型算例的各客户离仓库具有一定距离，客户呈集中分布，各区域内的临近客户大都由同一车辆配送；R 类型与RC 类型算例的客户呈随机分布，各车辆首先服务离仓库距离最近的客户，再依次服务距离较远的客户。

4.2.2 开放式车辆路径策略与封闭式车辆路径策略的对比分析

为分析开放式车辆路径策略的有效性，采用多类型算例将本文算法进行开放式车辆路径策略与封闭式车辆路径策略（车辆从仓库出发，完成配送任务后回到原仓库）的对比实验，计算结果如表2所示。表2中各符号的含义同表1所示。

根据表2的实验结果可知：

（1）所有算例中，开放式车辆路径策略求得的总配送成本（TC）要远远低于封闭式车辆路径策略求得的值，平均低10.32%，最高要低19.89%（算例R208），最少要低3.56%（算例C106）。

（2）开放式车辆路径策略求得的各算例车辆总使用时间（VUT）要远远低于封闭式车辆路径策略求得的值，平均低9.06%，最高要低12.51%（算例RC204），最少要低4.17%（算例R207）。

（3）开放式车辆路径策略求得的各算例车辆总行驶距离（VTD）要远远低于封闭式车辆路径策略求得的值，平均低24.25%，最高要低38.97%（算例C105），最少要低11.36%（算例R208）。

（4）开放式车辆路径策略求得的各算例车辆使用数量（VN）与算法运行时间（RT）要优于封闭式车辆路径策略求得的值。因此，开放式车辆路径策略能有效降低生鲜电商的总配送成本，节约车辆使用时间，缩短车辆行驶距离，减少车辆使用数量。

4.2.3 不同车辆使用成本计算标准的对比分析

为验证采用车辆总使用时间作为车辆使用成本计算标准的合理性，在所有参数不变的前提下，采用不同类型算例将本文方法与以车辆总行驶距离作为车辆使用成本计算标准方法进行对比实验。各算例实验结果如表3所示。表3中各符号的含义同表1所示。

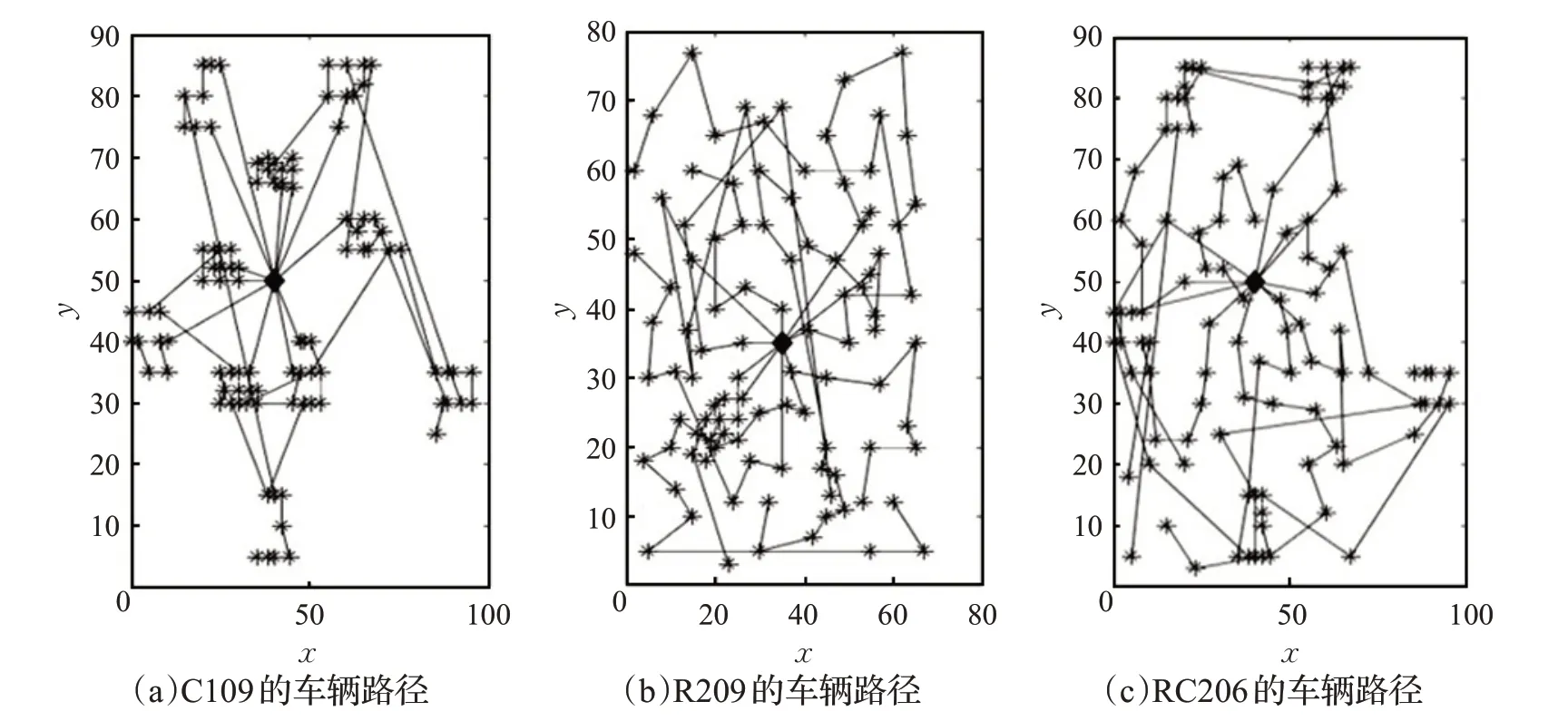
图3 不同类型算例的车辆路径规划

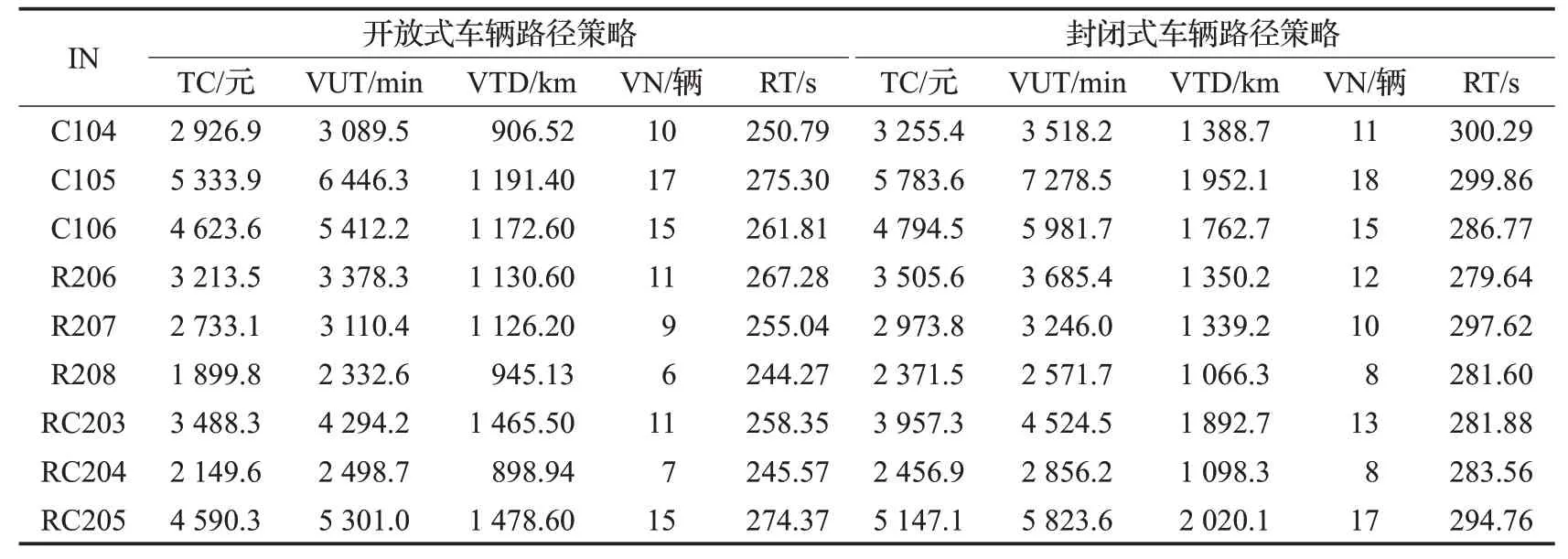
表2 开放式车辆路径策略与封闭式车辆路径策略的计算结果

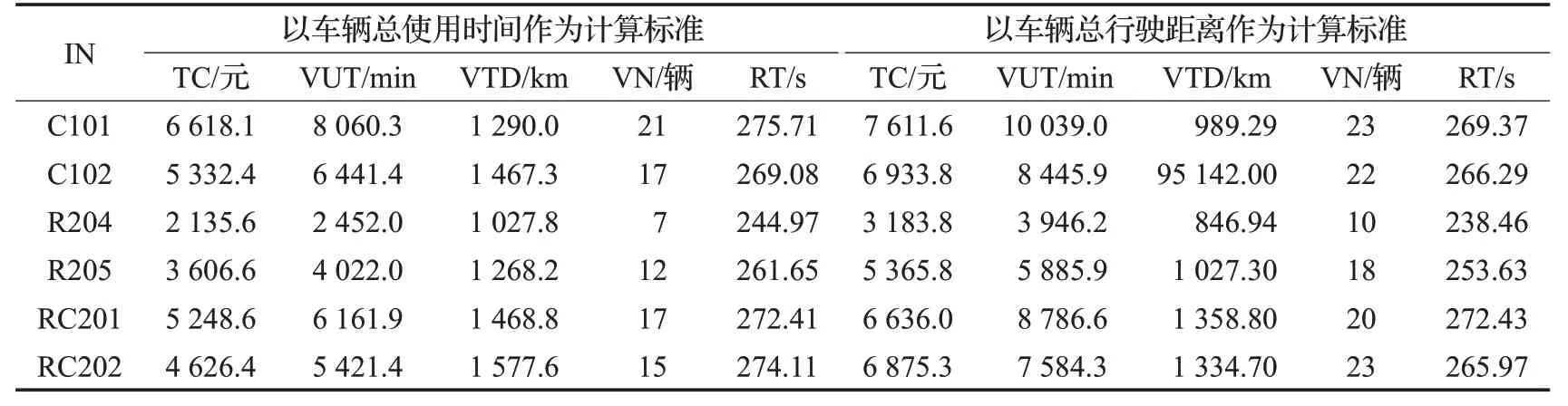
表3 车辆使用成本的不同计算标准的计算结果

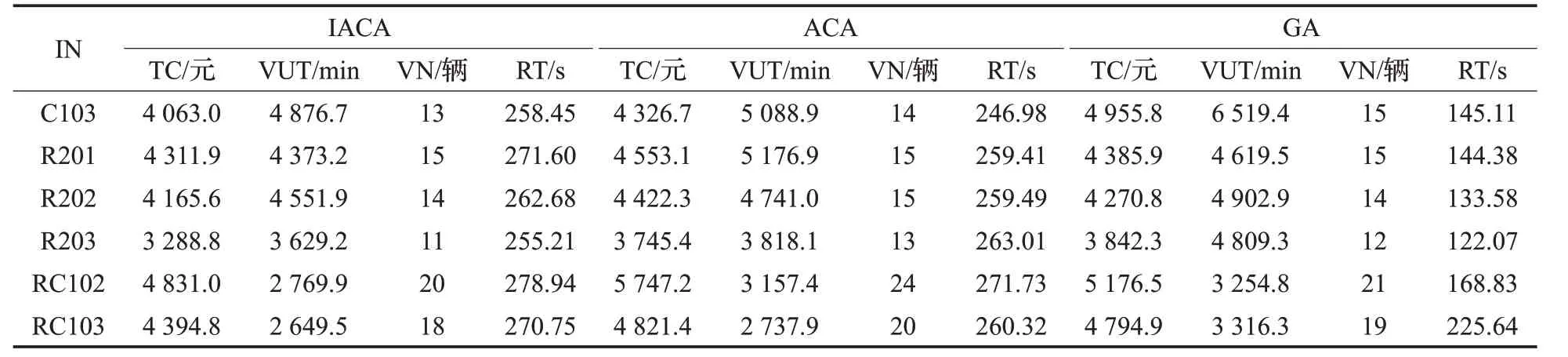
表4 不同算法的计算结果

由表3的计算结果可知：（1）在不同的计算标准下，本文算法都能求解出各种标准下的满意解。（2）以车辆总使用时间（VUT）作为车辆使用成本计算标准求得的各算例总配送成本（TC）要远远低于以车辆总行驶距离（VTD）作为车辆使用成本计算标准求得的解，平均要低25.91%，最多要低32.92%（算例R204），最少要低13.05%（算例C101）。（3）根据车辆使用数量（VN）的计算结果，以车辆总使用时间（VUT）作为车辆使用成本计算标准求得各算例的车辆使用数量（VN）要远远低于以车辆总行驶距离（VTD）作为车辆使用成本计算标准求得的解。说明在时变路网条件下，应使用车辆总使用时间作为车辆使用成本计算标准。

4.2.4 不同算法的对比分析

为验证本文改进蚁群算法（IACA）的可行性与合理性，另外编写了求解OTDVRP 的遗传算法（Genetic Algorithm，GA）程序。在所有参数不变的条件下，将本文IACA与文献[23]的蚁群算法（ACA）、GA进行对比分析。ACA设定转移规则里面仅有信息度浓度启发式因子与能见度启发式因子，没有自适应信息素启发式因子和期望启发式因子。设定GA 的种群数量为100，变异概率为0.1，交叉概率为0.9，迭代次数为600次。各算例的计算结果如表4所示。表4中所有符号的含义同表1所示。

根据表4 的计算结果可知：（1）关于总配送成本（TC），IACA 求得各算例的值最优。比ACA 求得的解平均要低9.02%，最多要低15.94%（算例RC102），最少要低5.29%（算例R201）；比GA 求得的解平均要低8.59%，最多要低18.01%（算例C103），最少要低1.68%（算例R201）。（2）关于车辆总使用时间（VUT），所有算例中IACA 求得的值最优。比ACA 求得的解平均要低7.35%，最多要低15.52%（算例R201），最少要低3.99%（算例R202）；比GA求得的解平均要低16.21%，最多要低25.19%（算例C103），最少要低5.33%（算例R201）。（3）IACA求解各算例的车辆使用数量（VN）显著优于其余两种算法求得的解。因此，IACA 在转移规则里面引入时间窗宽度启发式因子优先服务时间窗较窄的客户，以及自适应信息素启发式因子和期望启发式因子增强蚁群算法搜索的全局性等方法能有效降低总配送成本，缩短车辆使用时间，减少车辆使用数量，具有可行性与合理性。

5 结论

本文首先根据城市路网的时变特性设计车辆行驶时间计算方法；再综合考虑客户需求量、时间窗、生鲜度限制与开放式路径等因素，以总配送成本最小为目标构建带鲜活度限制的OTDVRP 优化模型，设计IACA 求解；采用多类型算例验证本文方法的可行性与有效性。仿真实验结果说明：（1）相对于封闭式车辆路径策略来说，开放式车辆路径策略能有效降低生鲜电商的总配送成本，节约车辆使用时间，缩短车辆行驶距离，减少车辆使用数量。（2）生鲜电商的客户主要在城市，城市路网具有时变特性，应使用车辆总使用时间作为车辆使用成本的计算标准。（3）根据IACA 与ACA、GA 的比较实验计算结果，IACA具有更好的优化效果。

进一步的研究将考虑车辆碳排放、油耗等环境因素，以期促进生鲜电商物流配送与环境保护的和谐发展。