基于改进跳点搜索策略的安全路径研究

黄智榜，胡立坤，张 宇，黄 彬

广西大学 电气工程学院，南宁530004

机器人路径规划是指机器人在有障碍物的工作环境中，按照一定的性能指标，寻找出一条从起始位置到目标位置的无碰撞路径。路径规划是移动机器人自主导航最关键的一个环节，也是机器人领域的研究热点[1]。路径规划常用的规划算法有A*算法[2]、蚁群算法[3]、人工势场法[4]、D*算法[5]、跳点搜索算法[6]、快速扩展随机树算法[7]和泡沫法[8]等。在静态的栅格环境中，A*算法规划效率最高。然而，由于A*算法在大型地图中需要对栅格地图的每个栅格点进行检测，造成需要检测的冗余节点过多。针对这个问题，Harabor等人[9]提出一种基于网格寻路的跳点搜索算法（JPS），该算法提出不必对每个栅格点进行检测，只需根据邻居裁剪规则筛选一些关键节点作为跳点进行评估，将评估后的最优跳点组合连接起来就是一条完整的最优路径。JPS算法尽管解决了A*算法计算冗余等问题，但是经研究发现该算法存在跳点数量多，规划的路径存在安全隐患等问题。

针对这些问题，文献[10]通过引入区域矩阵，将障碍物之间的中点作为跳点，使跳点与障碍物保持一定的距离，规划出安全的路径。但是该方法完全舍弃算法的路径寻优性能只考虑路径的安全性能。文献[11-12]提出双向跳点搜索算法，进一步减少了跳点的数量，加快了跳点搜索算法的搜索速度。然而，该方法没有综合考虑路径的安全性能。本文提出一种改进JPS算法，该算法通过改进跳点的筛选规则，将障碍物膨化处理，更改算法的行进模式，得到一条综合性能最优的路径。最后，通过仿真和实验验证了算法的可行性。

1 传统的JPS算法

1.1 邻居裁剪规则

JPS算法是通过搜索跳点来代替向四周扩展节点的一种改进A*算法[13]，JPS算法的本质是通过避开一些冗余节点，来减少所需要计算的节点数量，提高算法的运行速度。如图1 所示，假设在空白的栅格地图中存在s到g的三条路径，每条路径都存在一个中间节点分别为a2、b2、c2，其中以经过节点b2的路径最短，所以只需检测b2节点而避开不必要的a2、c2节点，就可以搜索出最优路径。这就是JPS算法的原理。

图1 跳点原理图示

利用跳点加速算法的搜索速度[14-15]，就是将A*算法中向邻节点扩展改为向四周搜索跳点扩展，就类似于现实中的城市十字路口一样，对每条路路口进行评估，选出评估值最低的路口，将它们连接起来就是一条到达目标点的最优路径。传统JPS 算法中采用邻居裁剪规则来对跳点进行筛选，其具体规则如图2 所示，其中灰色不需要查询的节点，白色为需要查询的节点。

图2 传统邻居裁剪规则

对比以上的图2（a）与图2（b）可以知道，在有障碍物的栅格环境中比无障碍物栅格环境需要多查询一个节点，称为被迫节点n，而无障碍物环境中查询的节点称为自然节点。从有障碍物裁剪可以看出，传统JPS算法寻找出的被迫节点比较靠近障碍物，且它们之间的路径经过障碍物的拐角，这影响了规划路径的质量。在文献[16]中跳点具有以下定义：

定义1 存在n ∈neighbours(x)，n不是x的自然节点，如果有len( p,x,n )＜len( p,n x )关系成立，则点n为被迫节点。

定义2 如果n以最小的值k，使得n=x+，并且下列条件之一成立，则节点n为来自节点x的跳点：（1）n为目标点。（2）节点n至少有一个邻居节点是被迫节点。（3）若为对角查询状态，且存在符合条件（1）和（2）的跳点时，则n为x的跳点。

根据以上的定义，传统的跳点分三种：分布在障碍物周围的被迫节点、存在被迫节点的自然节点、目标点。

1.2 跳点的评估函数

通过邻居裁剪规则可以从栅格地图中挑选出一些关键节点作为跳点，但是还需对跳点进行评估和计算，增强算法的启发性。假设已知起点s、目标点g、当前节点n以及父节点p，则算法搜索当前节点的实际代价为：

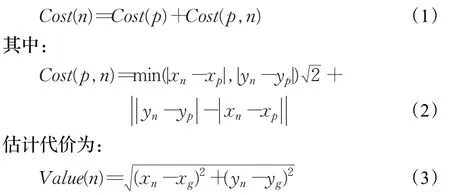
由以上几个公式就可得出跳点的评价函数为：

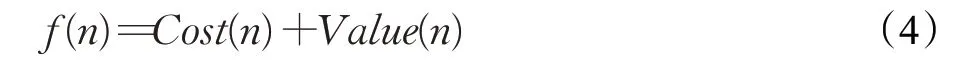
通过评价函数挑选出最优的跳点组合，连接起来就是一条起点到目标点的最优路径，其具体的算法模型如图3所示。模型中红色栅格为跳点，利用跳点能够在地图上构建出一条起始点到目标点的无碰撞最优路径。

图3 传统JPS算法

1.3 碰撞危险度评估模型

为了评估机器人路径的碰撞风险程度，采用二维高斯模型来建立危险度函数[17]，其模型如下：

其中，M为影响范围内障碍物的个数，ρ(xi,xobs)是路径当前点到障碍物的最近距离，d0是障碍物的影响范围，与机器人的机身大小相关，α、β决定着碰撞对机器人造成危险程度，由机器人的速度矢量以及障碍物的质材决定。本文取α=3，β=1，N=100。

2 改进的JPS算法

2.1 改进路径的行进方式

在传统的JPS算法中，路径的行进模式是固定的八邻域行进模式，这种模式好处在于能够简洁形象的显示算法的优劣性，但是却增加了规划路径的长度。故在本文中选择与实际较相符合的无限邻域行进模式[18]，即只要两个跳点之间没有障碍物，就能够直接将跳点相连形成路径。这种行进模式的优点在于能够缩短算法的路径长度和减少路径的转弯次数。

2.2 改进的邻居裁剪规则

在传统JPS算法中，机器人按照一个质点来处理，只能沿着8个方向移动。但是在本文中，机器人并不是一个质点，而是具有一定形状的物体。所以在使用传统的邻居裁剪规则时，机器人会与障碍物碰撞。本文基于对路径安全性能的考虑，将位于障碍物拐角处的两个传统跳点结合形成新类型的跳点。具体如图4所示。

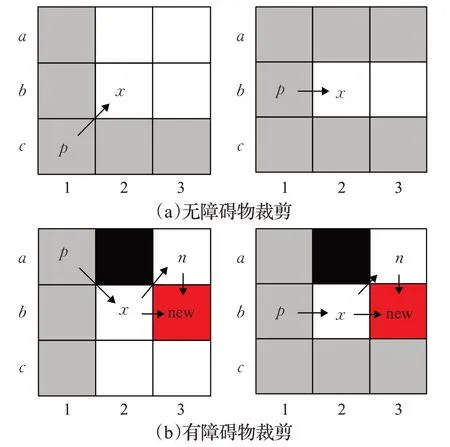
图4 改进的邻居裁剪规则

如图4（b）所示，在有障碍物的栅格环境中，将传统跳点结合形成新类型的跳点，新选取的跳点具有以下的几个优点：

（1）跳点之间的路径与障碍物保持一定的距离，使得规划路径的安全性能得到很大的提高。

（2）跳点位于障碍物尖角处，使其容易被检测出来，提高了算法的稳定性。

（3）跳点的辐射范围大，使算法搜索目标的能力增强，迭代次数变少，搜索速度增加。

2.3 改进算法流程

本文使用无限邻域行进模式构成路径，其改进的算法流程如下所示。

（1）初始化地图信息map，根据地图规格对障碍物进行膨化处理，设定起点s以及目标点g，并将起点s加入Open列表中。

（2）搜索Open 中实际代价与估计代价和最小的节点n，将n加入Closed列表并删除Open列表中的n。

（3）基于父节点n向四周扩展，具体为向四个倾斜方向扩展，即地图的右上、右下、左上、左下四个方向，并且每扩展一步的同时向相应的方向搜索，将搜索到的跳点加入到跳点集合中。

（4）删除跳点集合中与父节点n的直接路径穿过障碍物的节点，确保可以用无限邻域行进模式构成路径。

（5）将跳点集合中的点添加到Open列表中。

（6）如果跳点集合中存在目标点g，则终止主程序并输出路径；否则回到步骤（2），直到找到目标点。

其效果如图5所示。

图5 改进算法模型

3 算法的仿真与实验

3.1 改进JPS算法的仿真与对比

3.1.1 复杂地图仿真

为了说明本文提出的改进JPS算法的效果，在同一台计算机（Windows10，Intel Core i5，内存4 GB）上进行仿真。分别在U 型地图（200×200）和大型楼层地图（530×530）上进行仿真。

如图6 所示，传统的JPS 算法规划的路径中存在一部分路径贴着障碍物，这部分路径会增加机器人行走时与障碍物碰撞的几率。而改进JPS 算法规划出来的路径则不存在这种问题，并且由于改进JPS算法减少了构成路径的跳点的数量，使得规划路径的转弯次数大大减少。为了排除实验的偶然性，分别在两个地图中各取50组不同的起点和目标点来进行仿真，并将一百组数据按路径长度排序，可以看到其数据根据地形以及路径长短的不同而变化，具体如图7、8所示。

图6 两种算法仿真

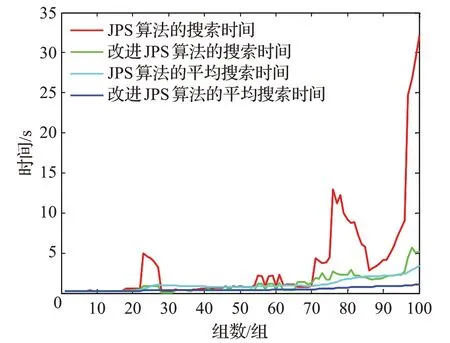
图7 算法搜索时间比较

在图7中可以看到在路径长度较短的实验组中，改进的JPS算法与其传统的JPS算法相比所用的时间基本上相差不大，并存在改进JPS 算法比JPS 算法搜索时间多的现象，但随着路径长度的增加，地图复杂程度的加大，改进JPS算法明显比传统JPS算法要快，最快可以达到一个数量级以上。同时，查看平均时间可以看到，在这一百组数据中，改进JPS算法的所用时间明显比传统JPS算法所用时间要少。将100组数据中的两种算法规划的路径长度进行对比，结果如图8所示。

可以看出，改进JPS算法搜索出来的路径平均长度都比传统JPS算法的路径平均长度要短，但是在路径长度短实验组中，有时会出现传统算法求出的路径比改进后的算法路径短的情况，这是由于本文算法对障碍物进行膨化处理导致的，属于正常的现象。随着路径长度的增加，地图复杂度的加大，这种现象会慢慢消失。为了对比两种算法的路径危险度，将由100组起讫点得出的路径进行等距离采样100 个点，设定影响范围d0=3，利用方程（5）和方程（6）来计算路径的危险程度，在路径危险度评估中，对每个点计算危险度，并将其加起来，就是整条路径的危险度评分。其具体数据如图9所示。

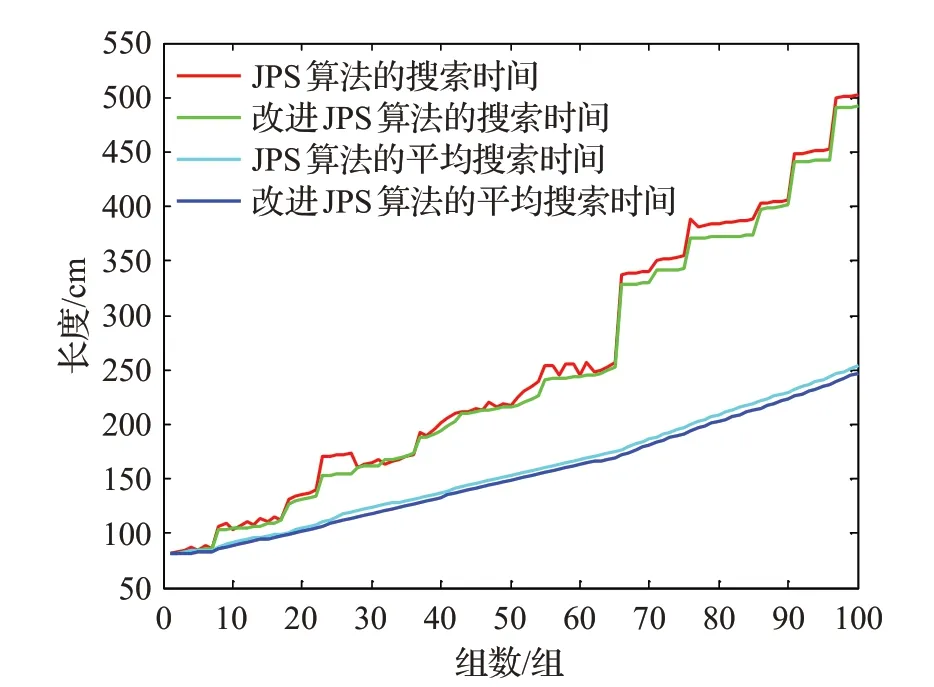
图8 算法搜索的路径长度比较

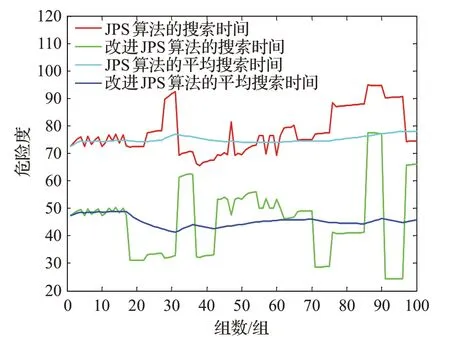
图9 路径危险度比较

如图9 所示，改进JPS 算法的危险度远远低于传统JPS算法的危险度，从上面的数据可以看到，改进JPS算法的平均路径危险度为45.69，传统的JPS算法的平均路径危险度为77.85，改进JPS算法比传统JPS算法危险度降低41.3%。其具体数据如表1所示。

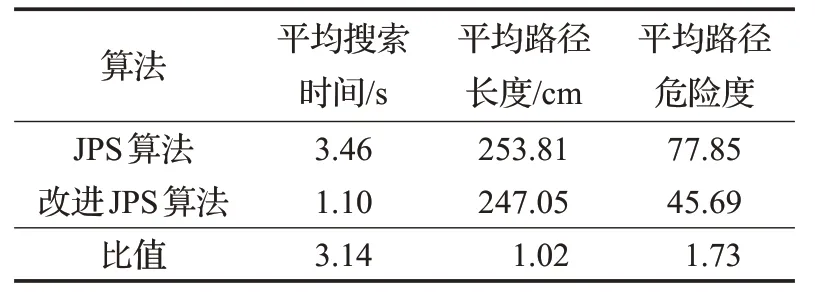
表1 实验组平均数据

3.1.2 不同规格地图仿真

为了探索改进JPS算法在不同规格地图中的性能，用MATLAB 在不同规格的简单地图中进行仿真，仿真数据如表2所示。

表2 不同规格地图仿真数据

从表2 看到随着地图规格的增加，改进JPS 算法搜索效率的比值减小，综合表1 的数据可以得出结论：改进JPS算法搜索速度的提升幅度与地图规格大小无关，与障碍物复杂程度有关，障碍物复杂程度度越高，搜索速度提升幅度越大。

3.2 实验测试

为了验证算法的有效性，在现实中搭建一个模拟的栅格地图，并将两种算法规划出来的路径导入两轮自平衡小车中进行实验。实验设备如图10 所示，其实验场景路线如图11所示。

图10 两轮平衡小车

可以看到，在图11（a）中，传统JPS算法的规划路径在拐弯处距离障碍物过近，导致两轮平衡小车的左轮与障碍物相撞，不能到达目标位置，故实际路径只有一小段。在图11（b）中，改进JPS 算法的规划路径与实际路径并不重合，在每个拐弯处，由于小车具有速度不能原地转弯，所以实际路径超出规划路径的范围，但是最后却能够成功地到达目标位置。

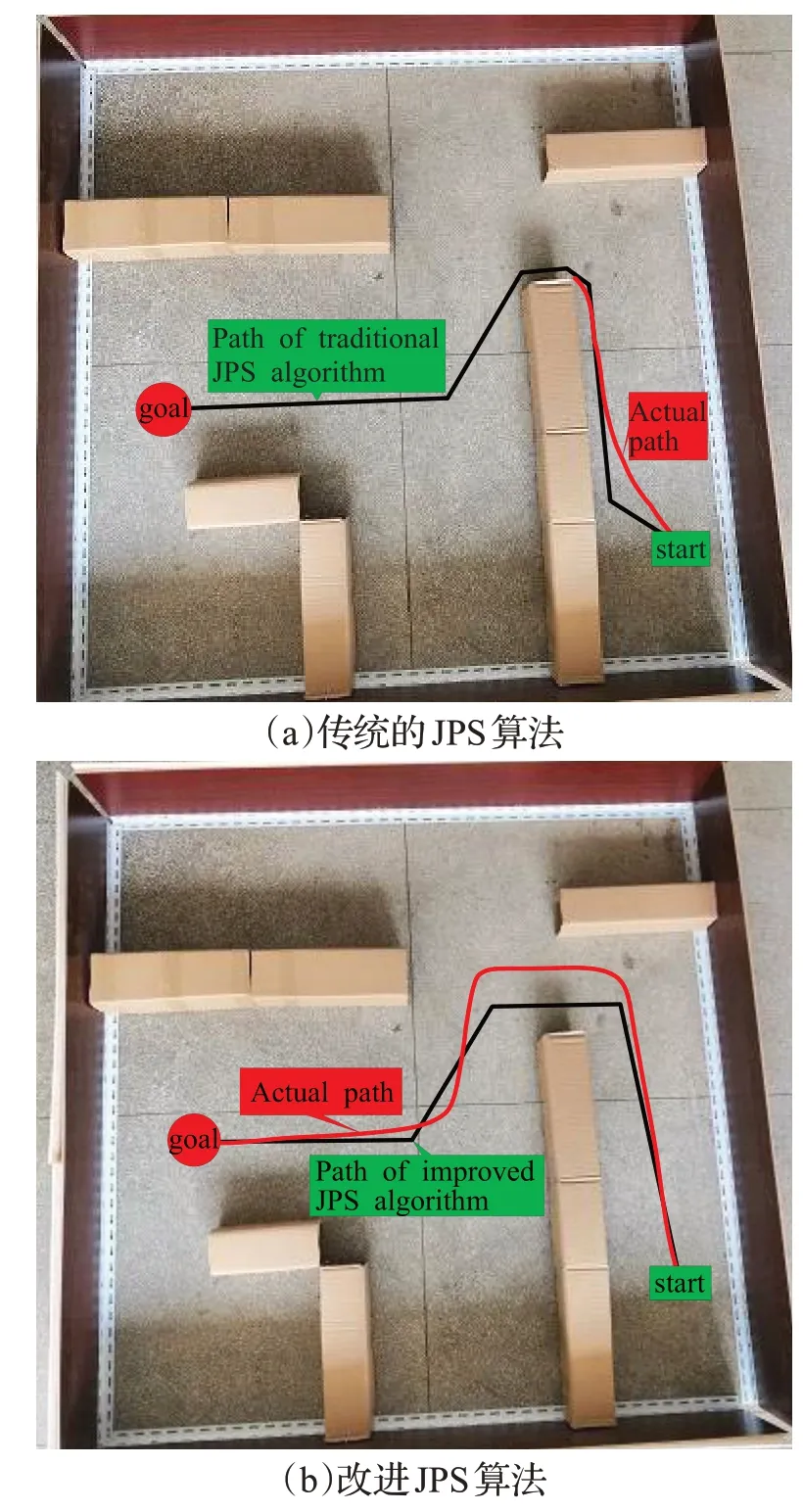
图11 规划出来的路径与实际路径比较

4 结论

传统的JPS 算法规划的路径存在安全隐患。本文在栅格地图中对移动机器人的工作环境进行建模，为了提高JPS算法的性能提出改进JPS算法。改进JPS算法能快速地生成一条起点到终点的无碰撞路径，这不仅解决了路径安全性的问题，还保留了传统JPS算法高效寻优的性能。通过在MATLAB 上仿真，验证了本文提出的改进JPS 算法无论是路径寻优还是安全性能都优于传统算法。