基于X-CT的非饱和水泥基材料 水分传输与渗透系数计算

杨 林，张云升，张春晓

(1.郑州大学水利科学与工程学院，郑州 450001；2.兰州理工大学土木工程学院，兰州 730050；3.中国人民解放军军事科学院国防工程研究院工程防护研究所，洛阳 471023)

0 引 言

基于重量法的毛细吸水测试是研究水分传输的传统试验方法，它能定量表征吸水量和吸水速率，但是无法监测水分传输的动态过程，也无法确定水分的传输高度[7]。随着现代分析测试技术的发展，核磁共振、中子成像和伽马射线成像逐渐被用来监测多孔材料的水分动态传输[8-11]。然而，核磁共振技术在硅酸盐水泥基材料中的应用存在局限性，水泥中的铁相会干扰信号；伽马射线成像只适用于吸水率较高的材料(通常大于5 g/100 cm3)；中子成像是研究水泥基材料水分传输较为理想的技术，但是全球的中子源非常有限，限制了该技术的广泛应用[12]。X射线计算机断层扫描(X-CT)是近年来发展较为迅速的无损检测技术，东南大学Zhang等[6]提出了利用X-CT联合Cs离子增强技术原位连续监测水泥基材料水分传输，不仅能观测水分传输的动态过程，而且能准确地判定水分传输的距离，为研究多孔介质的水分传输提供了可靠的测试手段。

本研究利用X-CT联合Cs离子增强技术原位监测非饱和水泥基材料水分传输过程，获得水分传输的毛细吸水系数，在此基础上通过理论推导提出了计算渗透系数的模型，并系统研究了水灰比、粉煤灰掺量、矿渣掺量和砂体积掺量对水泥基材料水分传输的影响。

1 渗透系数理论模型

在压力梯度下，多孔介质的水分传输通常用达西定律进行描述[13-14]：

(1)

式中：VF为水的流速，m/s；K为材料的固有渗透系数，m2；ΔP为压力差，Pa；x为水分传输的距离，m；η为水的粘滞系数，0.001 Pa·s(20 ℃)。

若在t时间内，水传输的距离为x，则流速VF亦可表示为：

(2)

由式(1)和式(2)联立，得到：

(3)

(4)

式(3)给出了水分传输距离与时间的关系，被命名为Lucas-Washburn方程[15]。k被称为毛细吸水系数(单位为m/s1/2)，它与材料的孔结构、水的表面张力和粘滞系数密切相关，是预测材料长期性能和耐久性的重要参数[6,10,16]。

当干燥的水泥基材料吸水时，其驱动力为毛细管作用力，此时压力梯度可以用拉普拉斯方程进行描述[17]：

(5)

式中：γ为水的表面张力，0.072 3 N/m(20 ℃)；r为毛细孔半径，m；θ为水与孔壁的接触角，对于水泥基材料，θ=0°。

由式(4)和式(5)联立，得到：

(6)

基于式(6)，水泥基材料的固有渗透系数可以由毛细吸水系数k和孔径r计算得到。其中，k可利用X-CT联合Cs离子增强技术得到；通过压汞法测得材料的孔信息，r等价于最可几孔径。

2 实 验

2.1 原材料

采用P·Ⅱ 52.5 硅酸盐水泥，其基本性能如表1所示。粉煤灰(FA)为某发电厂产出的二级灰，矿渣为市售的S95级磨细粒化高炉矿渣(GGBFS)。以上原材料的化学成分和粒度分布分别如表2、图1所示。采用河砂制备砂浆，细度模数为2.96。

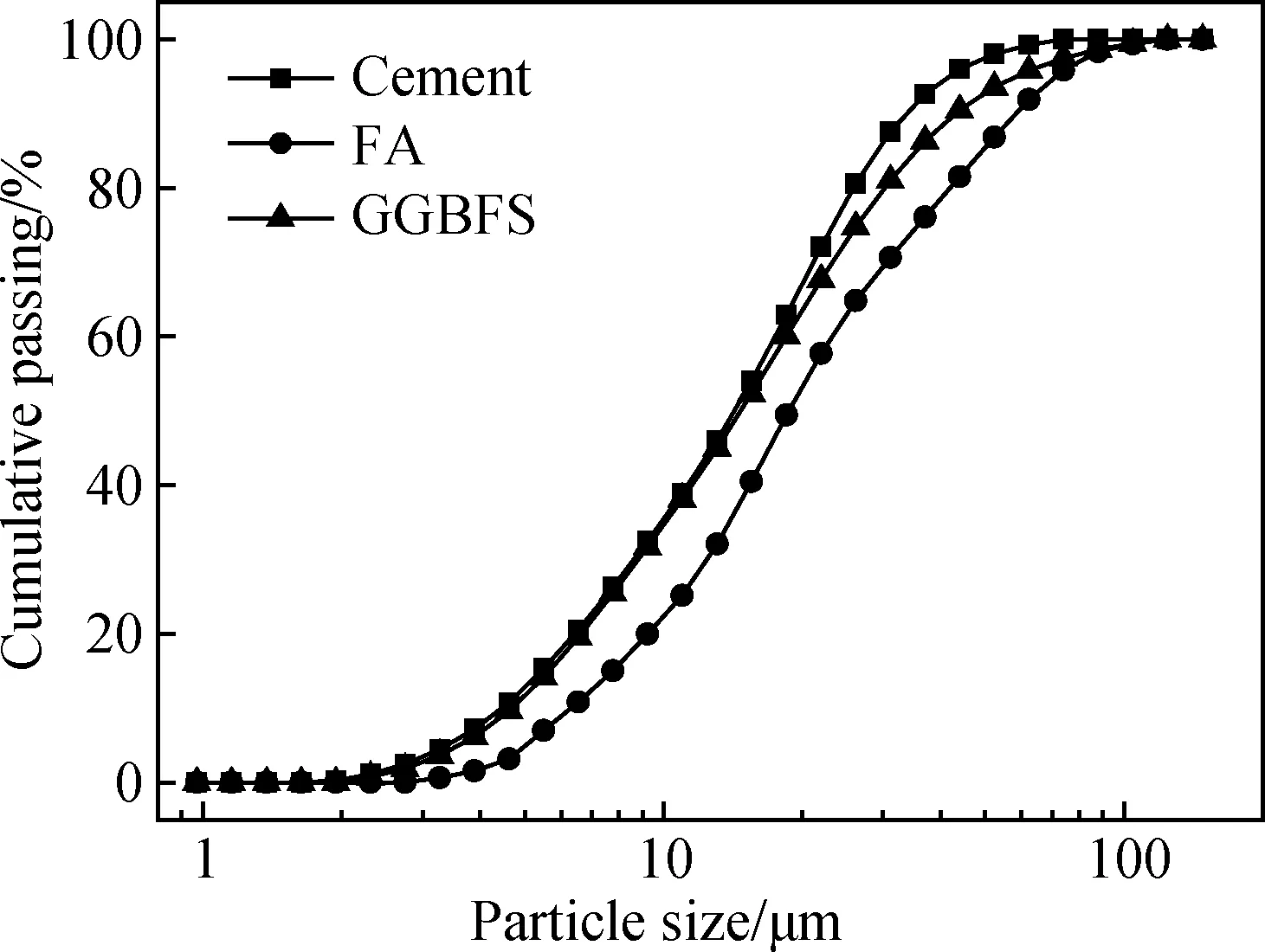
图1 原材料的粒度分布Fig.1 Particle size distribution of raw materials

表1 水泥的基本性能Table 1 Basic properties of cement

表2 原材料的主要化学成分Table 2 Main chemical composition of raw materials

2.2 配合比与试样制备

表3为设计的9组配合比。其中：PP1、PP2、PP3用于研究水灰比(W/C)对水分传输的影响；在PP2配比的基础上，采用粉煤灰等质量取代水泥，取代率分别为10%、30%、50%，用于研究粉煤灰掺量对水分传输的影响，即PF1、PF2、PF3；同样地，采用30%的矿渣等量取代水泥，与同等掺量的粉煤灰进行对比;MP1、MP2是砂体积掺量(VS)分别为20%、40%的砂浆，水灰比为0.45不变，用于探究砂体积掺量对水分传输的影响。

按照表3所示配合比成型尺寸为100 mm × 100 mm × 100 mm的试件，其中PP1、PP2、PP3、MP1、MP2在(20±1) ℃、相对湿度≥95%的养护室内养护至60 d，而PF1、PF2、PF3、PS在相同的条件下养护至90 d，使胶凝材料充分水化。

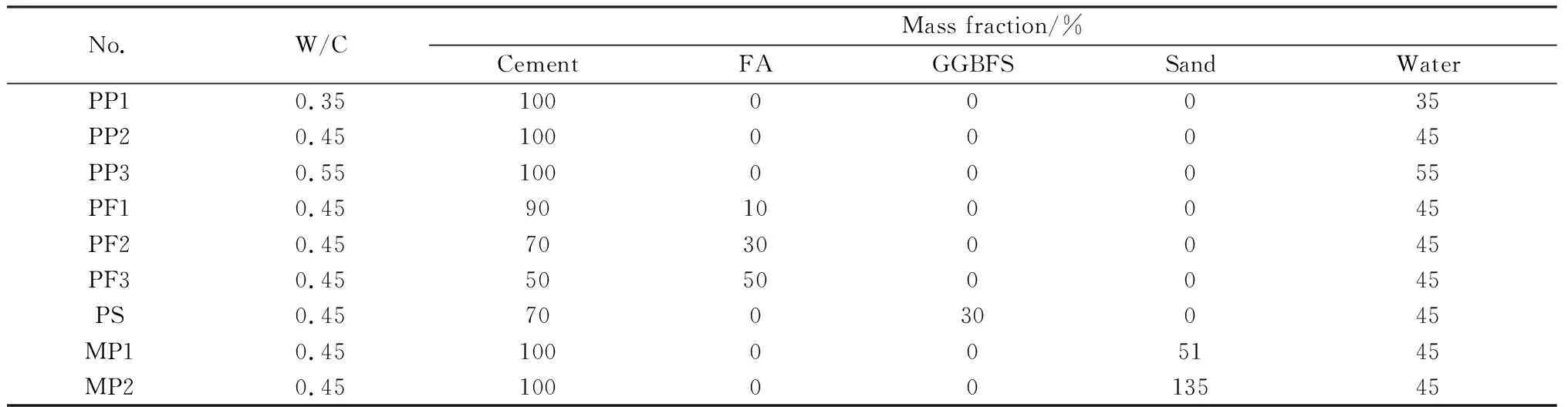
表3 配合比Table 3 Mix proportions

2.3 测试方法

2.3.1 压汞法

采用压汞法测试硬化水泥净浆和砂浆的孔结构。首先从养护完毕的试件中切割出尺寸为8 mm × 8 mm × 16 mm 的试样，在干燥箱中于60 ℃干燥72 h以上，然后利用AutoPore IV 9500压汞仪测试其孔结构，汞的表面张力和接触角分别为0.485 N/m、130°。

2.3.2 X-CT联合Cs离子增强技术

采用文献[6,18]所述的X-CT联合Cs离子增强技术原位连续监测水分在非饱和水泥净浆和砂浆中的传输。从养护完毕的试件中切割出尺寸为20 mm × 20 mm × 80 mm 的试样，在干燥箱中于60 ℃干燥至恒重，然后采用环氧树脂将试样的四个侧面和一个端面密封，另一个未密封的端面作为吸水面，使水分沿一维方向传输，如图2所示。所用设备为德国YXLON公司的Y.CT Precision S X-CT，X射线管工作的电压、电流分别为195 kV、0.34 mA，将样品放置在样品台上加入质量分数为5%的CsCl水溶液后开始计时，原位连续监测，每间隔30 min扫描一次，基于获得的CT图像判定水分的传输高度，具体参见文献[6]。

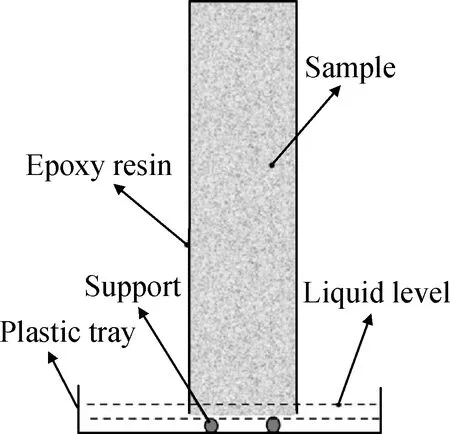
图2 基于X-CT的试样吸水Fig.2 Water absorption of sample based on X-CT

3 结果与讨论

3.1 水灰比对水分传输的影响

图3为采用X-CT联合Cs离子增强技术获得的不同水灰比硬化水泥浆体吸水过程中水分传输距离x与暴露时间t的关系。显然，x与t1/2呈线性关系，直线的斜率即为毛细吸水系数k。如图3所示，当水灰比从0.35增加到0.55时，硬化水泥浆体的毛细吸水系数从2.07×10-4m/s1/2增大到3.22×10-4m/s1/2，增长率达到56%。水灰比大小直接影响硬化浆体的孔结构，进一步影响浆体的吸水性能。通过孔结构测试，结果如图4所示，当水灰比从0.35增加到0.55时，硬化浆体的最可几孔径从34.3 nm增加到113.5 nm，且总孔隙率从12.01%增加到29.24%。水灰比增大，浆体的孔径与总孔隙率增大，且孔的连通性增加，浆体吸水过程中的毛细吸水系数增大。

图3 不同水灰比硬化水泥浆体水分传输距离与时间的关系Fig.3 Water uptake distance as a function of exposed time for cement pastes with different W/C

图4 不同水灰比硬化浆体的孔结构Fig.4 Pore structures of hardened cement pastes with different W/C

根据获得的毛细吸水系数和孔结构信息，采用本文所构建的理论模型，计算得到不同水灰比硬化浆体的固有渗透系数，如图5所示。当水灰比从0.35增加到0.55时，硬化浆体的固有渗透系数从2.54×10-18m2增加到2.03×10-17m2，增大了1个数量级。因此，降低水灰比是提高水泥基材料抗渗透性能的关键，也是保证严酷环境下混凝土结构长寿命的有效手段。

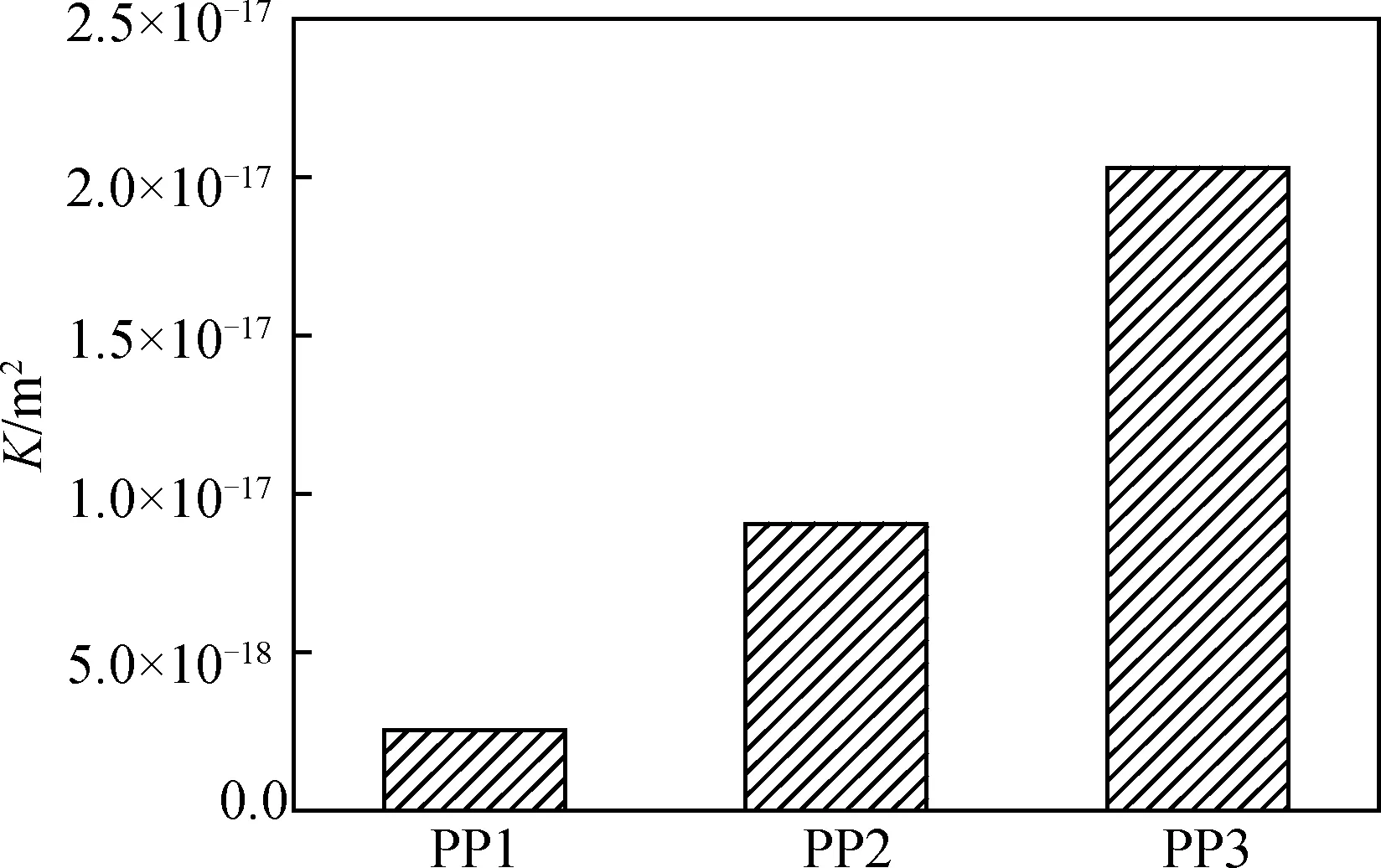
图5 不同水灰比硬化水泥浆体的固有渗透系数Fig.5 Intrinsic permeability coefficients of hardened cement pastes with different W/C

3.2 矿物掺合料对水分传输的影响

图6为掺粉煤灰、矿渣硬化水泥浆体的水分传输距离与时间的关系。可以看出，当粉煤灰的掺量从10%增加到30%时，浆体的毛细吸水系数从1.85×10-4m/s1/2下降到9.93×10-5m/s1/2，下降了46%；然而，当粉煤灰掺量增加到50%时，浆体的毛细吸水系数又有所增加，达到1.29×10-4m/s1/2，但仍小于掺10%粉煤灰的硬化浆体，且远小于同水灰比纯水泥浆体。图7为浆体的孔结构，当粉煤灰掺量为10%、30%、50%时，硬化浆体的最可几孔径分别为27.8 nm、18.2 nm、16.6 nm，总孔隙率分别为17.35%、17.83%、25.75%。根据孔结构与毛细吸水理论分析，当粉煤灰掺量从10%增加到30%时，虽然浆体的总孔隙率无显著变化，但孔径明显变小，故毛细吸水系数下降；而当粉煤灰掺量增加到50%时，硬化浆体的孔径没有明显下降，但总孔隙率显著增加，提高了孔的连通性，降低了水分传输通道的曲折度，因此毛细吸水系数再次增大。

图6 掺粉煤灰、矿渣硬化水泥浆体的水分传输距离与时间的关系Fig.6 Water uptake distance as a function of exposed time for cement pastes with FA and GGBFS

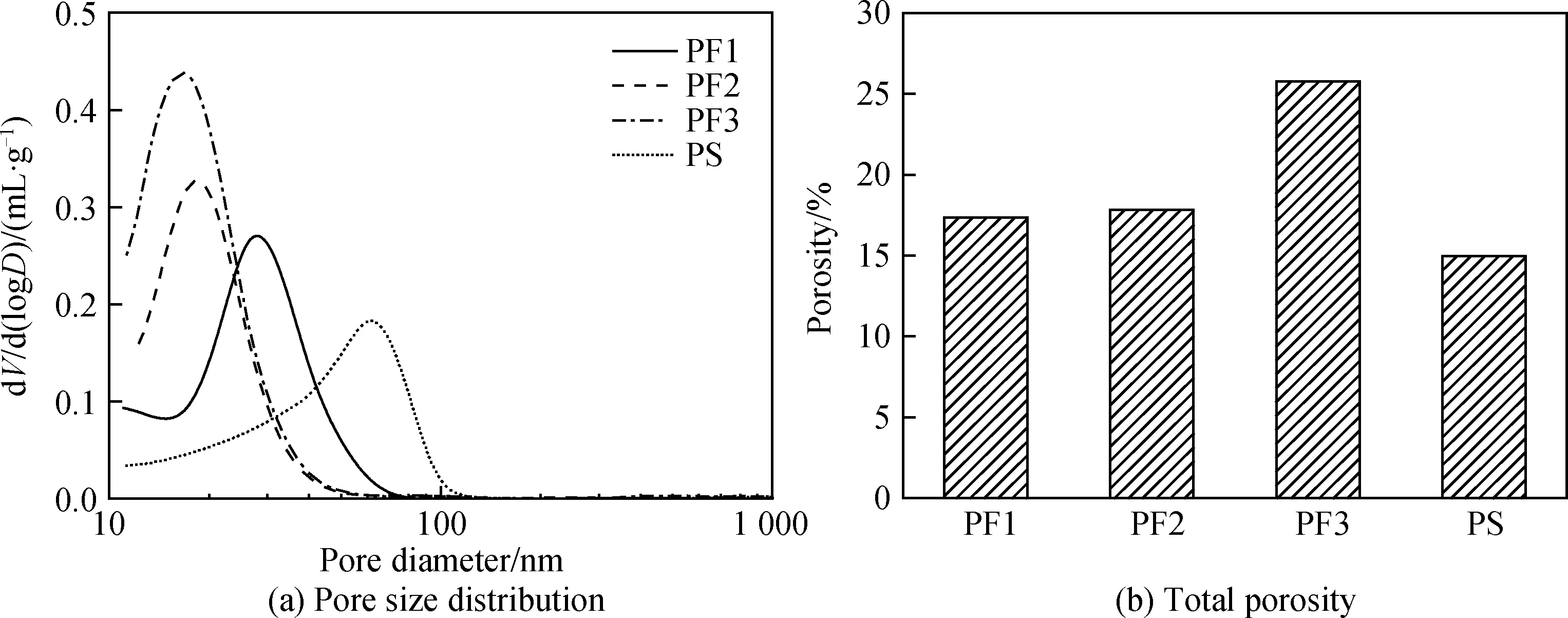
图7 掺粉煤灰、矿渣硬化浆体的孔结构Fig.7 Pore structures of hardened cement pastes with FA and GGBFS

为进一步研究矿渣对硬化浆体水分传输的影响，将30%的粉煤灰替换为同等掺量的矿渣，其硬化浆体的毛细吸水系数为1.46×10-4m/s1/2，如图6所示。显然，在同等掺量的情况下，掺矿渣硬化浆体的毛细吸水系数大于掺粉煤灰浆体。从孔结构上看，当掺入30%矿渣时，硬化浆体的最可几孔径为62 nm，总孔隙率为14.97%，尽管总孔隙率稍小于掺入30%粉煤灰的硬化浆体，但孔径要远大于后者，因此其毛细吸水系数较大。

图8为掺粉煤灰、矿渣硬化水泥浆体的固有渗透系数。从图中可以看出，粉煤灰掺量对硬化水泥浆体固有渗透系数的影响与对毛细吸水系数的影响具有一致性，当粉煤灰掺量从10%增加到30%时，硬化浆体的固有渗透系数从1.64×10-18m2下降到3.08×10-19m2，而当粉煤灰掺量达到50%时，固有渗透系数再次增加。当矿渣掺量为30%时，硬化浆体的固有渗透系数为2.28×10-18m2，比同等粉煤灰掺量的硬化浆体高1个数量级。

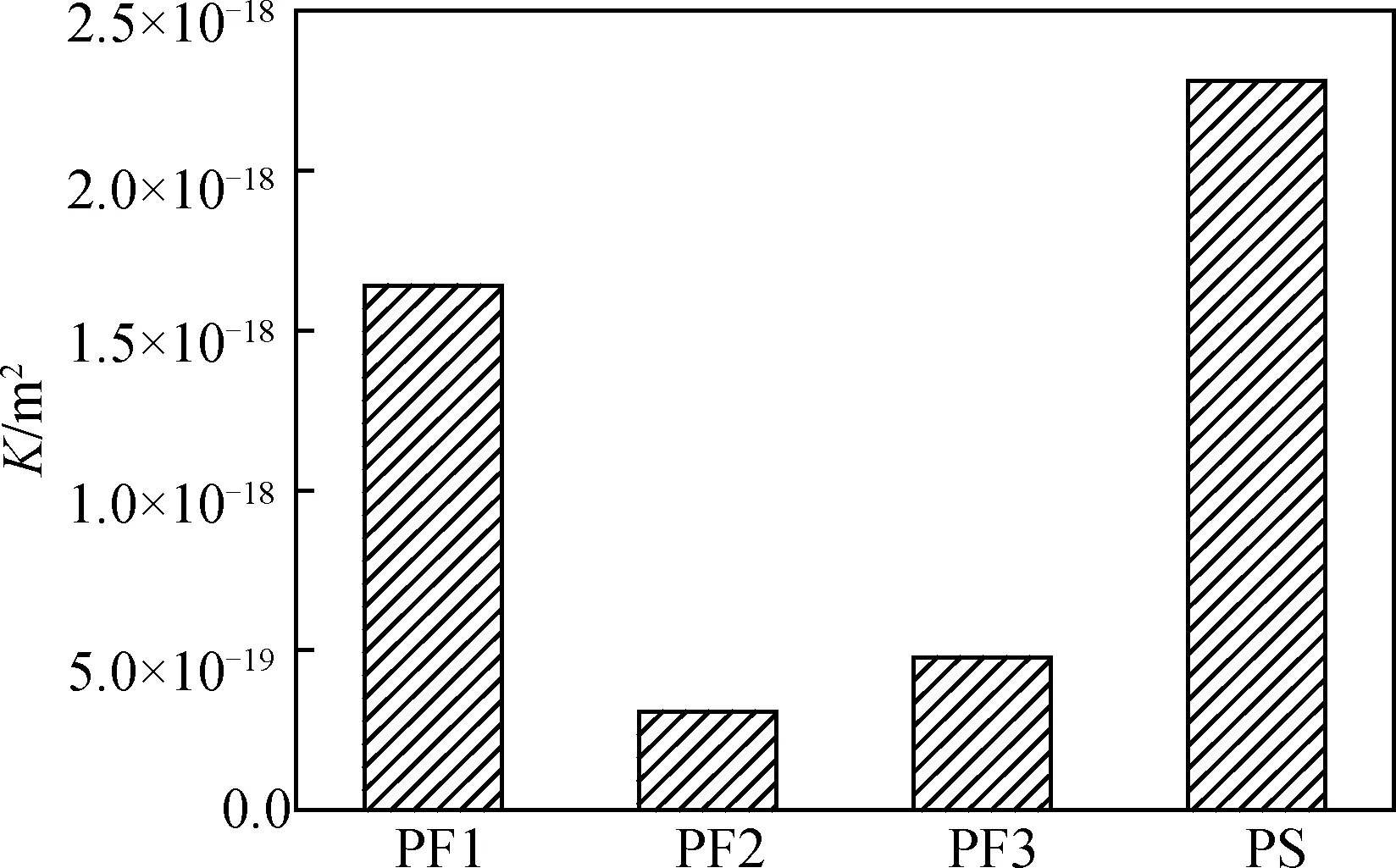
图8 掺粉煤灰、矿渣硬化水泥浆体的固有渗透系数Fig.8 Intrinsic permeability coefficients of hardened cement pastes with FA and GGBFS

以上结果表明，粉煤灰的掺入能有效降低浆体的水分传输速率，减缓有害介质向材料内部的迁移速率，但粉煤灰的掺量宜控制在合适的范围内，以不超过30%为最佳。同等掺量时，矿渣的掺入对浆体的孔径没有表现出细化作用，它对水泥基材料抵抗有害介质侵蚀的能力差于粉煤灰。在工程应用时，粉煤灰与矿渣复掺是提高水泥基材料长期性能和耐久性的有效措施，前者能细化孔径，后者对降低总孔隙率有利。

3.3 砂体积掺量对水分传输的影响

图9为砂体积掺量分别是0%、20%、40%时砂浆的水分传输距离与时间的关系。随着砂体积掺量的增加，砂浆的毛细吸水系数从2.83×10-4m/s1/2下降到1.65×10-4m/s1/2。砂体积掺量不同时砂浆的孔结构如图10所示，当砂体积掺量从0%增加到40%时，砂浆的最可几孔径从65.4 nm增加到108 nm，而总孔隙率没有表现出显著的变化，分别是18.13%、19.78%、15.47%。如果单独从孔结构分析，随着砂体积掺量的增加，砂浆的毛细吸水系数应呈增大的趋势，但这与试验结果相反。另一个不容忽视的原因是，砂的吸水性与浆体相比可以忽略，砂掺入后对浆体的吸水起到了稀释作用，同时增大了水分传输路径的曲折度，降低了水分的传输速率[5]。

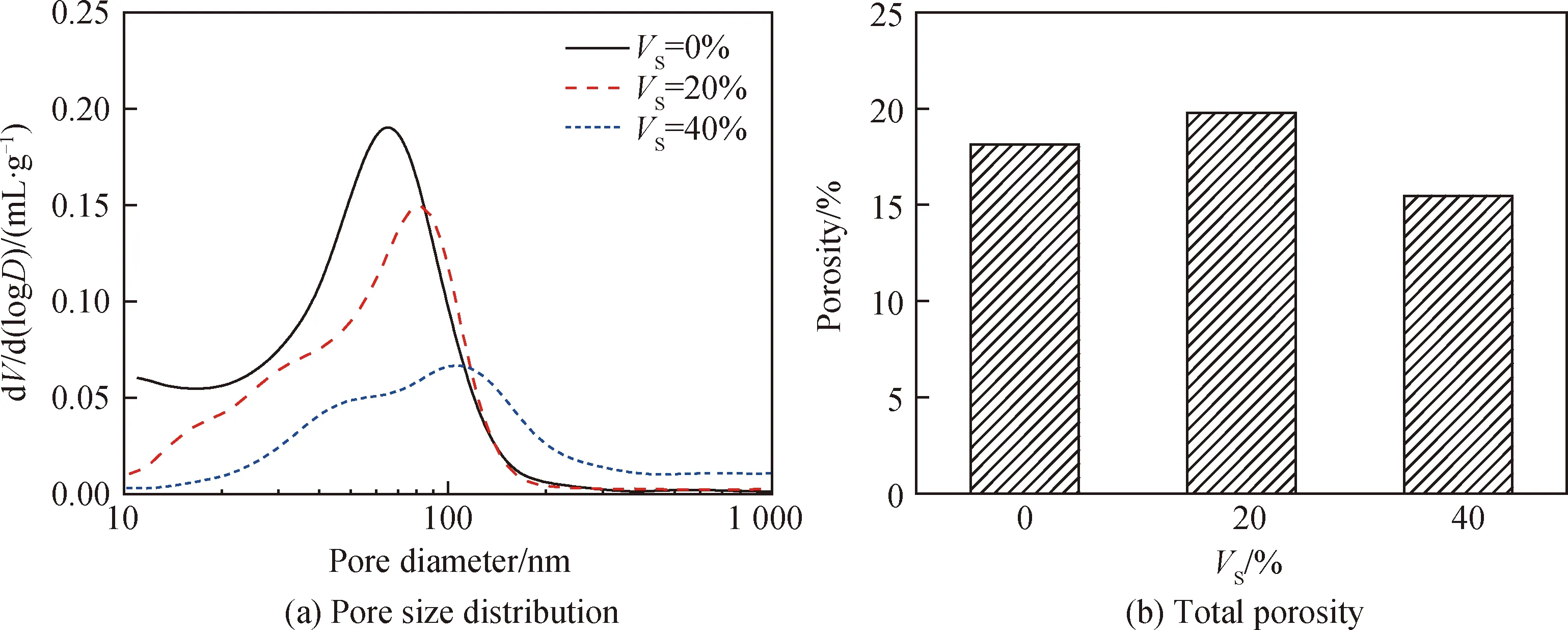
图10 砂体积掺量不同时砂浆的孔结构Fig.10 Pore structures of mortars with different volume fractions of sand

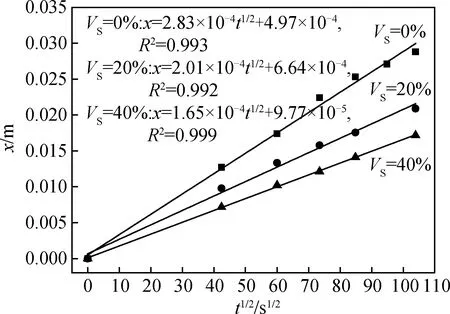
图9 砂体积掺量不同时砂浆水分传输距离与时间的关系Fig.9 Water uptake distance as a function of exposed time for mortars with different volume fractions of sand

为了进一步分析砂体积掺量对砂浆水分传输的影响，定义了相对毛细吸水系数k/k0，其中k0是砂体积掺量为0%时的毛细吸水系数。砂体积掺量对相对毛细吸水系数的影响如图11所示。从图中可以看出，随着砂体积掺量的增加，k/k0逐渐减小，二者的关系可以用式(7)进行表达：

(7)

从图11可以看出，当砂的体积掺量从0%增加到40%时，k/k0<1-VS，这是砂的曲折度效应所致。当砂的体积掺量为20%时，k/k0与1-VS的差距最大，而后随着砂体积掺量的增加，k/k0与1-VS的差距逐渐缩小，这是因为砂浆的界面过渡区体积分数逐渐增大。由式(7)计算得到，当VS=42.4%时，k/k0=1-VS，此时砂浆的界面过渡区完全连通。该研究结果较好地验证了Hall等[19]提出的分析模型，且为Abyaneh等[5]的数值模拟结果提供了有力的证据。

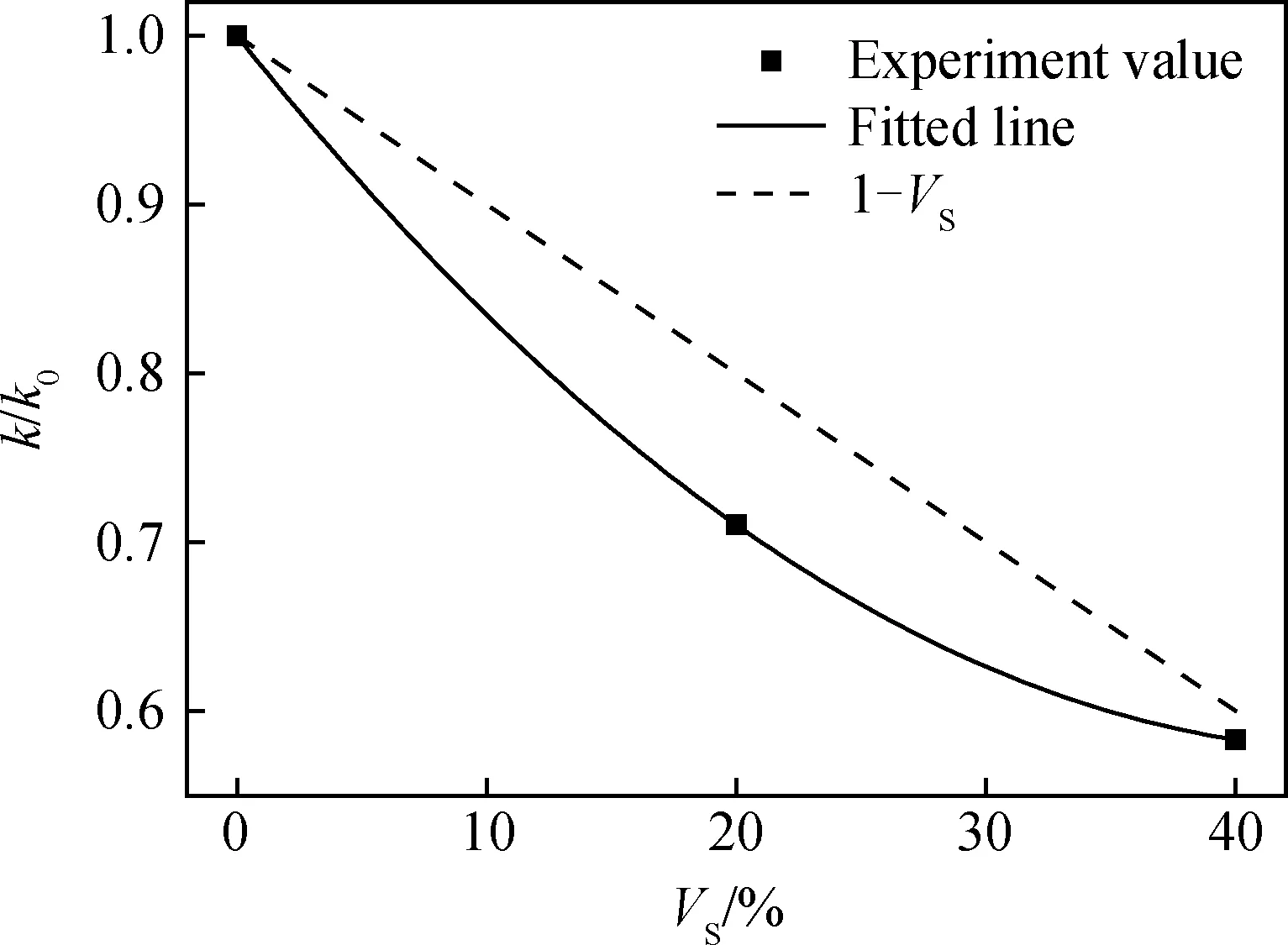
图11 砂体积掺量对砂浆相对毛细吸水系数的影响Fig.11 Effect of sand volume fractions on the relative capillary coefficient of mortar

图12为砂体积掺量不同时砂浆的固有渗透系数。当砂体积掺量从0%增加到20%时，砂浆的固有渗透系数从9.06×10-18m2下降到5.38×10-18m2，下降了40.6%；而当砂体积掺量达到40%时，砂浆的固有渗透系数为5.07×10-18m2，相对于砂体积掺量为20%时几乎无变化。

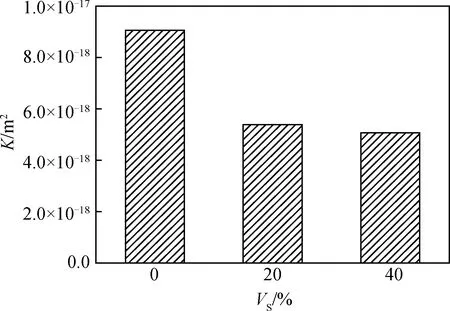
图12 砂体积掺量不同时砂浆的固有渗透系数Fig.12 Intrinsic permeability coefficients of mortars with different volume fractions of sand

4 结 论

(1)X-CT联合Cs离子增强技术是研究水泥基材料水分传输的可靠方法，在此基础上通过理论模型的构建，可进一步计算材料的固有渗透系数。

(2)当水灰比从0.35增大到0.55时，硬化水泥浆体的毛细吸水系数从2.07×10-4m/s1/2增大到3.22×10-4m/s1/2，而固有渗透系数增大1个数量级。

(3)粉煤灰的掺入能有效降低浆体的水分传输速率，但粉煤灰的掺量宜控制在合适的范围内，最佳掺量为30%；当矿渣掺量为30%时，对浆体的孔径没有表现出细化作用，其固有渗透系数比同等粉煤灰掺量的硬化浆体高1个数量级。

(4)当砂体积掺量从0%增加到40%时，因稀释效应和曲折度效应的存在，砂浆的毛细吸水系数和固有渗透系数均明显下降；而当砂体积掺量大于42.4%时，砂浆的界面过渡区完全连通，砂对水分传输失去了曲折度效应的影响。