双桶洗衣机脱水桶动力学特性研究

张强 杨洪永 熊瑞 王扬河

珠海格力电器股份有限公司 广东珠海 519070

1 引言

双桶洗衣机，即半自动洗衣机，有两个盛衣桶，其中一个是洗涤桶，另一个是脱水桶，由两个电机分别驱动。洗涤桶完成洗涤后，需要用户从洗涤桶中取出衣物，然后放入脱水桶进行脱水。与全自动波轮洗衣机、滚筒洗衣机相比较而言，双桶洗衣机自动化程度较低，但因为洗净度高、价格低廉，在农村依然有一定的市场空间。而且双桶洗衣机不会像全自动洗衣机那样，内外桶/筒之间容易积藏洗涤污垢，长时间使用会出现“脏桶”的情况发生。双桶洗衣机洗涤空间清洁干净，不会出现二次污染的情况。

双桶洗衣机自动化程度较低还体现在脱水桶脱水时没有自动调整衣物偏心的功能，在向脱水桶投放衣物时，多数情况下需要用户手动将衣物调整均匀，减小偏心，提高脱水成功率，否则会因为偏心过大而出现脱水桶撞击箱体的现象，即“打桶”现象。撞击剧烈时会导致“打桶”一直持续，使电机无法继续升速进行正常脱水，更甚者会造成脱水桶的破损。有时在进行衣物脱水时，需要用户多次调整衣物平衡才可以成功进行脱水。

用户对双桶洗衣机脱水打桶的问题一直有较大抱怨，而且洗衣机洗涤、脱水容量逐渐增加，脱水转速也因电机技术的发展而得以继续提升[1]，这就对脱水系统抗偏心能力提出了更高的要求，双桶洗衣机脱水系统抗偏心能力的大小成为双桶洗衣机脱水性能的重要参数之一。本文首先从理论出发，将双桶洗衣机脱水桶的运动模型简化为平面二自由度模型，并进行数学建模和求解，探讨了一些降低脱水桶振动的措施，然后利用仿真技术，对脱水桶进行基于模态的频率响应分析来验证一些推导结论，提供了一种研究双桶洗衣机脱水桶振动的方法。

2 脱水桶动力学建模

2.1 模型简化

双桶洗衣机脱水桶如图1所示，脱水桶通过置于桶下的电机直接驱动，电机通过电机支架悬置于三个或四个带橡胶套的弹簧支座上。

脱水桶稳定运行时，桶部件径向振幅可视为沿圆周方向处处相等，故可将其运动简化为平面运动，在简化平面内有两个运动分量，桶部件的平动和转动，由此可将双桶洗衣机脱水系统的运动模型简化为平面二自由度模型，平动分量标记为x(t)，转动分量标记为θ(t)，下面对此平面二自由度模型进行数学建模，建立其运动方程。

2.2 动力学建模

将脱水桶弹簧分解为竖直方向和水平方向两种弹簧，刚度分别标记为k1，k2，偏心质量标记为m，脱水桶总质量标记为M，脱水桶总质心的高度标记为h1，偏心高度标记为h2，脱水桶总高度标记为h，脱水桶半径标记为R，如图2所示。

2.2.1 基本假设

本动力学建模有以下两点基本假设：

（1）以分析脱水桶的稳态振动为主，因阻尼对稳态振动影响较小，故动力学建模中忽略支座的阻尼c，仅考虑支座刚度k；

（2）脱水桶顶端安装有液体平衡环，此处分析暂不考虑平衡环的影响。

2.2.2 运动方程

脱水桶的平面二自由度运动形式如图3所示，根据达郎贝尔原理，建立系统的力平衡方程和绕O点的力矩平衡方程，即建立起此平面二自由度模型的运动微分方程：

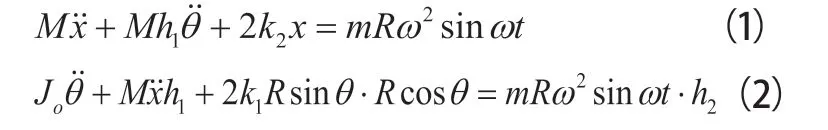
式（2）中Jo为脱水桶绕O点的转动惯量，将式（1）、式（2）整理为：

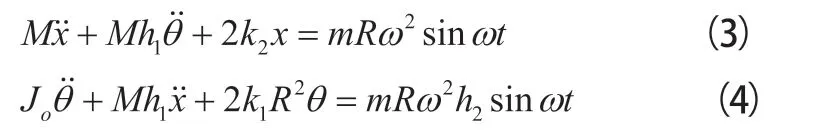
将式（3）、式（4）写为矩阵形式：

式（5）即为双桶洗衣机脱水桶平面二自由度模型的运动微分方程。

2.2.3 模型求解

现在对式（5）所示运动方程进行求解，并根据求解结果对脱水桶动力学特性进行研究，因为是无阻尼系统，假设式（5）的解为：

将式（6）代入式（5）得：

进一步写为：

设定：

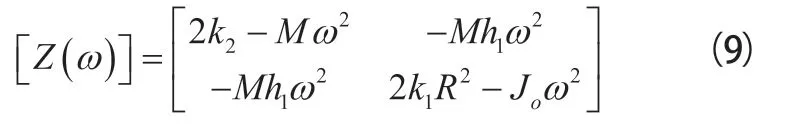
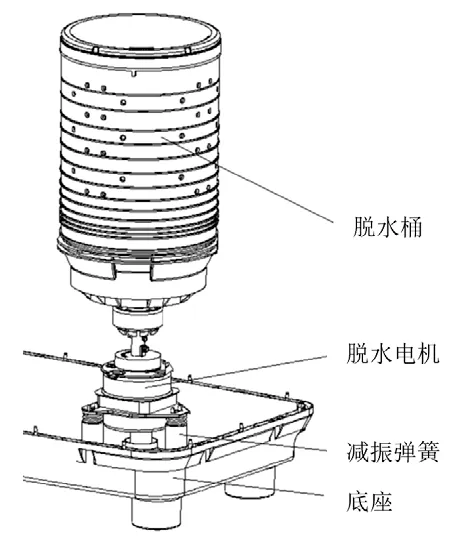
图1 双桶洗衣机脱桶结构图

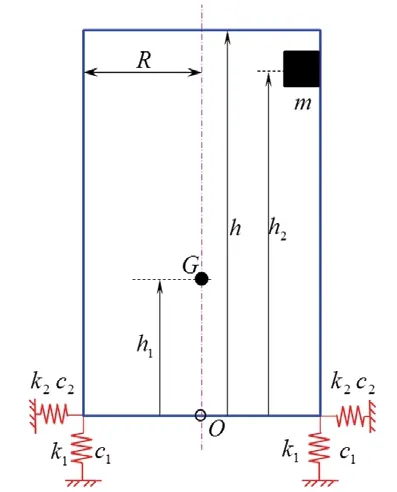
图2 脱水桶动力学简化模型

图3 洗衣机悬挂系统平面二自由度模型

将式（9）代入式（8）得：

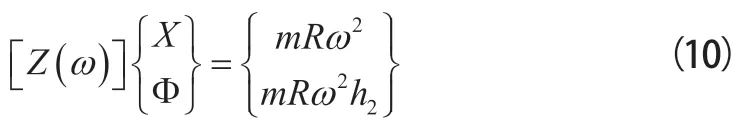
式（10）的解为：

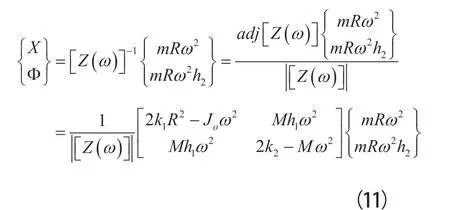
针对式（10），满足如下关系的ω值，则为运动方程的特征值：

运动方程的特征值即为运动系统的固有频率，因为所建模型为二自由度系统，存在两阶固有频率，将其分别标记为ω1和ω2，则存在如下关系：

图4 X(ω)幅频曲线

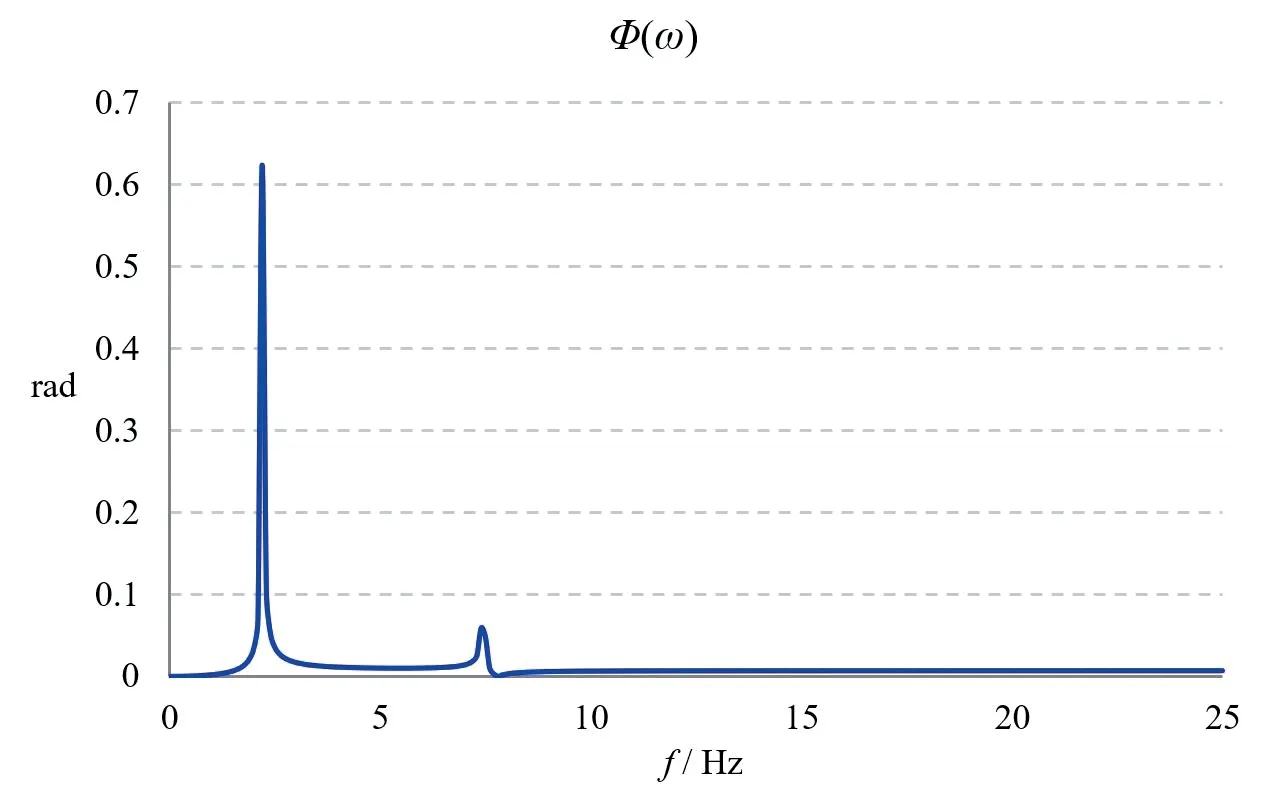
图5 Φ(ω)幅频曲线

运动方程的最终解为：

桶部件顶端的合位移为：

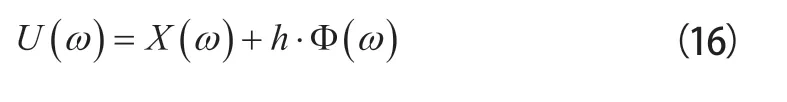
3 动力学特性研究

假设某双桶洗衣机脱水桶各参数如下：M=4 kg；m=0.05 kg；Jo=0.5 kg·m2；R=127.5 mm；h=600 mm；h1=100 mm；h2=600 mm；k1=3000 N/m；k2=4000 N/m。基于此脱水系统进行双桶洗衣机脱水桶的动力学特性分析。

3.1 振型分析

使用设定的脱水系统各参数，求解式（12），可得运动方程的特征值，即系统的共振圆频率：

使用设定参数和求解的第一、二阶共振圆频率，根据式（14）、（15）、（16）绘制X(ω)、Φ(ω)、U(ω)的幅频曲线，分别如图4、图5、图6所示，脱水桶的振动在经历低速段的两阶共振后，在高速段振幅趋于稳定。

3.2 质心高度对脱水桶振动的影响

根据已经建立的脱水桶平面二自由度模型，探讨一些参数对脱水桶振动的影响，本节考察脱水桶质心位置对振动的影响：在脱水桶不同高度位置附加均匀质量1 kg，附加质量高度分别为：H1=300 mm，H2=400 mm，H3=500 mm，H4=600 mm（脱水桶总质心高度h1，转动惯量Jo，运动方程特征值ω1、ω2都随附加质量的高度改变而发生改变，计算中已考虑了这些参数的变化），如图7所示，比较并分析各工况下脱水桶的振动。

根据式（16）及已定义的脱水桶各已知参数，计算附加上述各均匀质量后的脱水桶顶部中心的振幅，为考虑偏心高度对结果的影响，分别计算了偏心高度h2为600 mm、200 mm两种工况，其幅频曲线分别如图8、图9所示，从计算结果可以看出，在高速稳态振动阶段，附加相同的均匀质量，附加质量位置越高，振幅越小。换言之，如果提高脱水桶的质心高度，可降低脱水桶的稳态振幅。

4 有限元仿真分析验证

4.1 有限元建模

使用仿真分析软件对某型号双桶洗衣机的脱水系统进行有限元仿真分析前处理，并进行模态仿真分析和基于模态的频率响应分析。具体的建模方法如下：

（1）脱水桶用Plotel单元描述其轮廓，并在其质心位置创建CONM2单元，将脱水桶的质量和惯性参数赋予该CONM2单元；

（2）电机亦用质量单元代替，在其质心位置创建CONM2单元，将电机的质量和惯性参数赋予该CONM2单元；

（3）弹簧不使用CELAS1弹簧单元描述，而是采取抽取弹簧螺旋线，用CBEAM单元划分1D网格的方法来描述，这样可同时考虑弹簧的轴向刚度及弯扭刚度；

（4）Plotel轮廓与脱水桶质心之间、脱水桶质心与电机质心之间、电机质心与弹簧梁单元之间使用RBE2刚性单元连接；

（5）进行基于模态的频率响应分析，分析中考虑了阻尼的影响，以模态阻尼的方式添加阻尼。

通过以上方式创建的脱水桶有限元模型如图10所示。

4.2 边界条件和载荷

（1）边界条件：在每支弹簧的底端施加固定约束（3个平动自由度、3个转动自由度全部约束）；

（2）载荷：频响分析中，在两个正交方向施加相位差为90°的简谐激励相当于施加一个旋转矢量，可用于模拟偏心产生的旋转离心力。激振力的幅值即为偏心离心力，见下式（17）：

假设Z方向为脱水桶的竖直方向，则在X、Y方向施加幅值为偏心离心力，相位相差90°的简谐激励。

4.3 模态分析

如图11所示，列出了模态分析中脱水桶前八阶模态，其中第一、二阶模态为各弹簧交替拉伸、压缩所表现出的脱水桶摆动（对应于平面二自由度模型中的θ(t)，第三阶模态为脱水桶绕竖直轴的转动，第四、五阶模态为弹簧横向运动所表现出的脱水桶平动（对应于平面二自由度模型中的x(t)），第六阶模态为弹簧同步拉伸、压缩所表现出的脱水桶上下跳动模态，在偏心激励（横向）作用下，易于激起第一（二）阶模态和第四（五）阶模态，即平面二自由度模型中的摆动（转动）模态和平动模态。

图6 合位移U(ω)幅频曲线

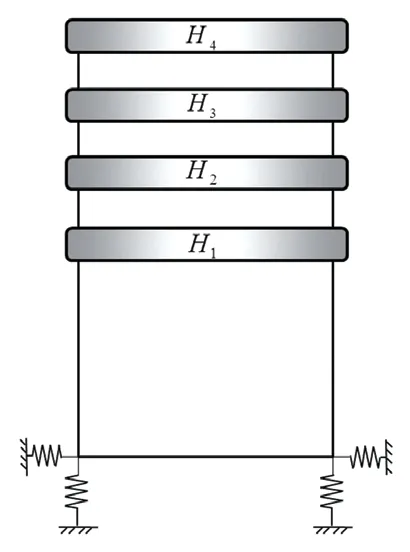
图7 脱水桶不同高度处附加均匀质量

图8 不同高度处附加均匀质量时脱水桶顶部合位移U(ω)幅频曲线（h2=600 mm）

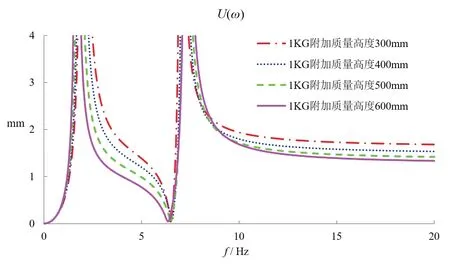
图9 不同高度处附加均匀质量时脱水桶顶部合位移U(ω)幅频曲线（h2=200 mm）

图10 脱水桶有限元模型

图11 模态结果汇总

图12 附件质量置于不同高度时的脱水桶顶端位移幅值频谱图

4.4 频响分析：附加质量对脱水桶振动的影响

在脱水桶上附加1 kg质量，将附加质量的高度位置由脱水桶底面逐步向上移动，输出附加质量置于不同高度下的脱水桶顶端位移幅值频谱图（如图12所示），可以看出，随着附加质量的位置抬升，脱水桶的稳态振幅明显降低，与所建立的数学模型结论一致。此外，因为所建立数学模型中未考虑阻尼的影响，只分析了稳态振幅的大小，仿真分析中考虑了阻尼效应，共振幅值在可以参考的合理范围内，从仿真分析结果中可以看出，随着附加质量高度的抬升，脱水桶第一阶、第二阶共振的共振幅值也随之降低，即附加质量措施，和提升脱水桶质心高度措施除了降低脱水桶稳态振幅外，也可以提升脱水桶启动阶段的抗偏心能力。

5 结论

（1）通过将双桶洗衣机脱水桶的运动简化为平面二自由度运动，从而建立了脱水桶的二自由度运动方程，对脱水桶的振型进行了分析，并得到了脱水桶顶端位移的计算公式，可以据此进行脱水桶稳态振幅的计算；

（2）根据所建立的运动方程，对脱水桶的动力学特性进行了研究，探讨了在脱水桶上附加质量环及质量环高度对脱水桶振动的影响，得出结论：脱水桶附加质量可以降低脱水桶的振动，而且附加质量位置越高，减振效果越明显；

（3）使用CAE技术进行了脱水桶动力学仿真研究，针对附加质量措施对脱水桶振动的影响，仿真分析结果与动力学方程求解的结果，其趋势是一致的，验证了所建立运动方程的合理性，同时提供了一种双桶洗衣机脱水桶的动力学仿真分析方法。