各向异性油藏考虑储层污染影响的水平井产能

孙恩慧

(中海石油(中国)有限公司天津分公司 渤海石油研究院,天津 300452)

在水平井开发生产过程中,如果储层出现污染,对水平井产能有很大影响[1]。目前国内外一些学者对水平井产能的预测进行了很多研究[2-6],但没有考虑地层污染对水平井产能的影响。汪子昊[7]分析了地层损害对水平井产能的影响,但文中假设水平井生产段的表皮因子是一个固定值,但在实际生产过程中,表皮因子沿生产段是非均匀分布的。黄世军[8]研究了考虑生产段表皮因子变化的水平井产能模型,但模型中没有考虑各向异性对水平井产能的影响。本文基于储层污染带的渗流模型,利用坐标变换原理,推导出新的局部表皮因子计算模型,利用该模型可以得到水平井总表皮因子公式,利用该公式修正Joshi产能公式。

1 储层污染表皮因子计算模型

假设水平井受污染后垂直井筒方向的剖面渗流模型,如图1所示。

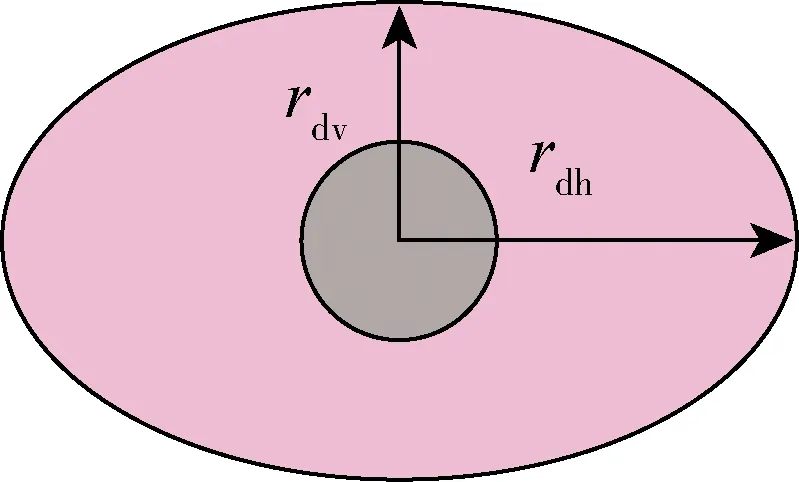
图1 水平井受污染后垂直井筒方向的剖面渗流模型

1.1 局部表皮因子的计算

假设在各向异性油藏中有一口长度L的水平井,储层污染区长半轴为rdh,则yz坐标系上稳态渗流方程为

(1)

式中，kz为垂向渗透率，10-3μm2;ky为水平渗透率,10-3μm2。

内边界条件为:

(2)

式中，rw为井筒半径，m;pwf为井底流压,MPa。在yz坐标系上,井筒周围的等压线为同心椭圆,引入uv坐标系,则储层污染区域的分布类似于井筒周围压力场分布,如图2所示。

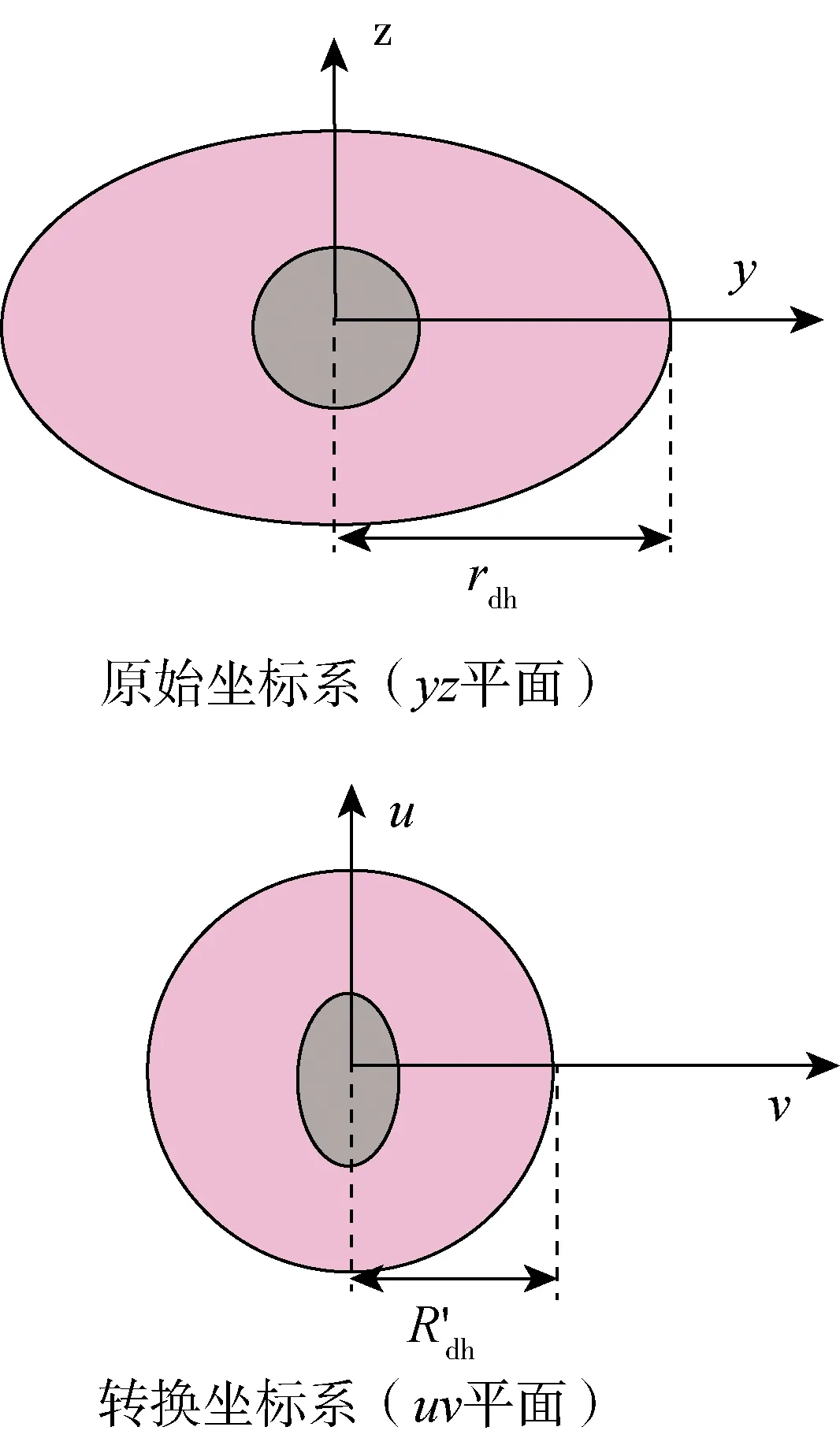
图2 坐标转换前后储层污染带示意图

引入uv坐标系,作坐标转换,有

u=(ky/kz)1/4z;v=(kz/ky)1/4y.

(3)

则(1)式变为

(4)

式(2)变为:

(5)

求解上述具有椭圆形内边界条件的拉普拉斯方程,需引入保角变换,将椭圆坐标系转变为ρθ坐标系,则

u=bcoshρcosθ;v=bsinhρsinθ.

(6)

当井筒处ρ=ρw时,由(6)式得

(7)

对比(5)式和(7)式得

(8)

椭圆形等压线平均半径可以定义为长轴与短轴的平均值,即

(9)

通过坐标变换后,根据水平井储层污染区域渗流特征,只要分别计算出井筒平均半径和储层污染带平均半径,就可以利表皮因子计算公式对其进行求解。

结合(8)式和(9)式,得到井筒平均半径为

(10)

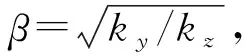
(11)

则(3)式坐标变换为

(12)

由(6)式得到等效各向同性地层中等压线的长轴和短轴分别为:

uo=bcoshρ;vo=bsinhρ.

(13)

对于椭圆形污染带,结合(12)式和(13)式,当ρ=ρd时,得到

(14)

结合式(9)和(14),则椭圆形污染带平均半径为:

(15)

利用文献[9]推导出各向异性地层下表皮因子的表达式为

(16)

式中,k为地层渗透率，10-3μm2;kd为污染带渗透率，10-3μm2。

综合式(11)、(15)和(16),得到水平井污染带局部表皮因子为

(17)

文献[10-11]中认为,污染带半径沿水平井井段方向分布不均匀,如图3所示。地层污染带半径为生产段x的函数,即rdh=rdh(x)。

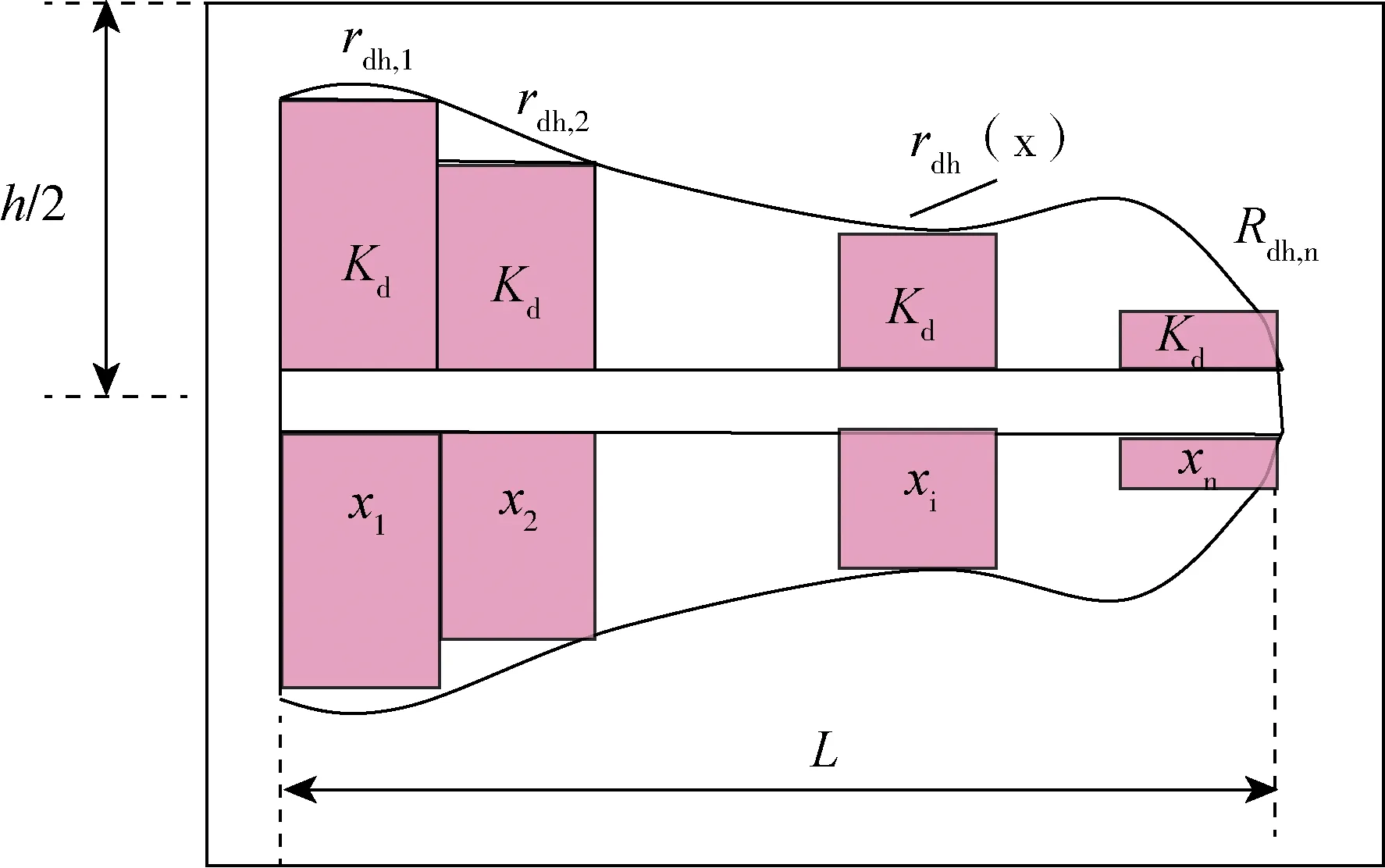
图3 污染带沿井筒分布模型

则(17)式变为

(18)

式中,Sd(x)为生产段x处的污染带局部表皮因子。

1.2 总表皮因子的计算

根据yz平面内任一位置,长度为dx井段的产量为:

(19)

式中，μ为原油黏度，mPa·s;Bo为原油体积系数；Δp为生产压差，MPa;h为油层厚度，m。

将(19)式在[0，L]积分得到全井的产量为

在此竞赛项目中，视频率先给出活动情境说明：本活动为大班幼儿美术命题画教育活动片段，因而活动分析主要从四个方面进行分析：

(20)

考虑表皮因子的水平井的产量为

(21)

结合(20)式和(21)式,得到污染带总表皮因子为

(22)

考虑各向异性对总表皮因子的影响,(22)式变为

ln[βh/rw(β+1)].

(23)

若计算总表皮因子,需要知道局部表皮因子沿井筒方向的分布情况。由于水平井趾端与钻井液接触时间较短,趾端无污染,而跟端与钻井液接触时间最长,污染最大。为了计算简便,假设钻井液最大侵入深度为Rmax,污染带半径沿井筒呈抛物线分布,那么污染带半径沿井筒方向分布函数为

(24)

将式(24)、(18)代入式(23),通过积分即可计算出总表皮因子。

2 考虑储层污染的水平井产能及影响因素

2.1 考虑储层污染的水平井产能公式

利用上面得到的总表皮因子的表达式,修正Joshi公式,得到考虑各向异性和储层污染影响的水平井产能新公式:

(25)

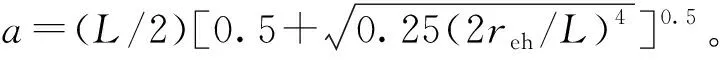
2.2 计算实例

利用文中局部表皮因子计算公式,结合以上水平井数据,可以作出局部表皮因子沿井段方向分布示意图(图4)。

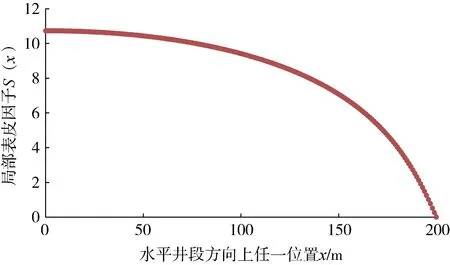
图4 污染带水平井局部表皮因子沿井筒方向分布图

由图4可以看出,污染带水平井局部表皮因子由跟端(x=0 m)到趾端(x=200 m)逐渐减小,主要原因是跟端与钻井液接触时间最长,污染最大,局部表皮因子最大,趾端与钻井液接触时间较短,污染最小,局部表皮因子最小。

将水平井基本参数带入式(23),计算出总表皮因子为5.9。利用笔者所推导的产能模型进行产量计算,与由其他常规水平井产能公式的结果进行对比,结果如表1所示。

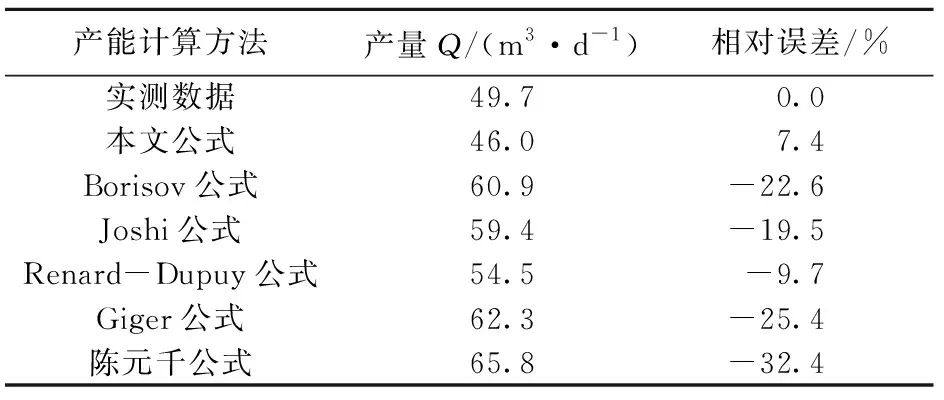
表1 各种方法计算水平井产量的结果对比

由表1可以看出,利用Borisov公式、Joshi公式、Renard-Dupuy公式、Giger公式以及陈元千公式计算出的产量与实际产量的相对误差较大,为-32.4%～-9.7%,主要原因是这些公式未考虑储层污染对储层渗透率的影响,因此产能预测结果偏高。由本文公式计算出的产量与产量的相对误差最小,仅为7.4%,所以本文公式在水平井储层受污染后产能预测方面具有较高的准确性与实用性。

2.3 影响因素分析

2.3.1 各向异性对水平井产能影响

图5为不同地层各向异性系数条件下水平井产能与水平段长度的关系曲线。从图中看出,当水平段长度一定时,随着各向异性系数的增加,水平井产能减小,这是由于油藏垂直方向渗透率减小导致垂直方向渗流阻力增大,使得水平井产能下降。

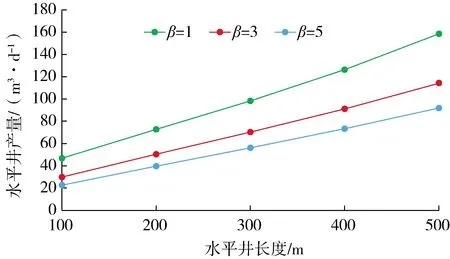
图5 不同地层各向异性系数条件下水平井产能与水平段长度的关系曲线

2.3.2 污染深度对水平井产能影响

图6为不同污染深度(钻井液最大侵入深度)下水平井产能与水平段长度的关系曲线。从图中看出,当水平段长度一定时,随着钻井液最大侵入深度的增大,水平井产能降低,分析其原因是随着钻井液侵入深度的增加,总表皮因子增加,水平井生产段附近地层的渗流阻力增加,水平井产能降低。因此,在水平井的钻井和完井过程中应注意储层的保护。

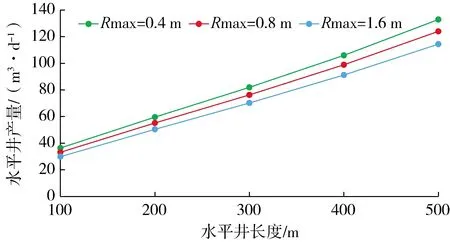
图6 不同污染深度下水平井产能与水平段长度的关系曲线

2.3.3 污染程度对水平井产能影响

图7为不同污染程度(地层渗透率/储层污染带渗透率)下水平井产能与水平段长度的关系曲线。从图中看出,当水平段长度一定时,随着污染程度的增大,水平井产能降低。主要原因是当污染程度增大后,水平井总表皮因子增加,水平段周围的渗流阻力就会增大,导致水平井产能降低。

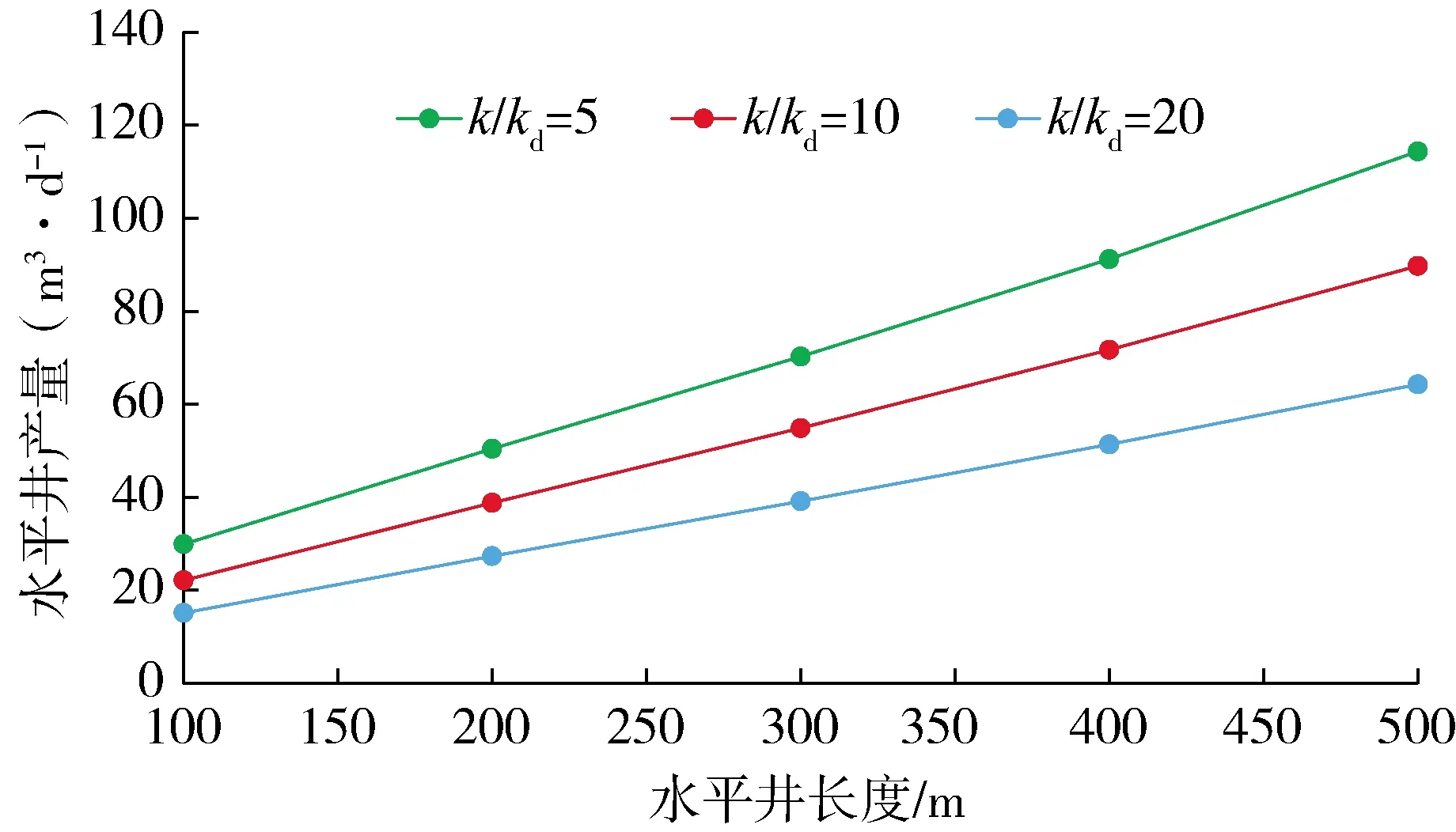
图7 不同污染程度下水平井产能与水平段长度的关系曲线

3 结 论

(1)利用坐标变换,推导出了新的局部表皮因子计算模型,利用该模型可得到水平井总表皮因子公式。

(2)得出了考虑油藏各向异性和储层污染的水平井产能计算公式,实例计算表明,该公式预测精度较高。

(3)在其他参数一定的条件下,随着各向异性系数的增加、污染深度和污染程度的增大,水平井产能减小。