基于模糊神经网络的导航数据融合算法仿真设计

张群芳

（沈阳理工大学自动化与电气工程学院 辽宁·沈阳 110159）

0 引言

导航系统各个传感器及信息处理平台，能够接受、融合并处理各类导航数据，导航数据具有明显的异构性。导航系统具有全天候、高精度、多功能等优点，在测角、测距、测速时，需要避免由多路径引起的观测误差和融合误差。如何提高数据的融合精度，是保证导航系统服务的关键。传统的模糊神经网络可实现无监督或监督学习，大大增加了及时性，但在融合大量异构数据时，容易造成局部最优，使得整体融合结果不准确。此外，导航数据融合需要对异构数据进行排序传输到置信链上，通过对数据属性的分析得到新的信息，并用于下一个融合节点的再次分析。异构数据的复杂性，导致融合处理信息时间过长，故异构导航数据融合需要根据实际情况选择一种或者几种算法组合的模式。因此，本文基于自适应模糊神经网络，利用粒子群优化参数学习，为导航系统接收的异构数据进行属性和特征值划分，对预处理过的数据进行有效融合，保证融合的收敛速度和准确性。

1 导航数据融合模型

导航数据融合模型采用分布式结构，如图1所示。导航系统信息中心接受目标区域中的异构导航数据，经过滤波预处理及时空配准后，导航数据进入融合中心进行数据融合输出。

图1：导航数据融合模型

2 基于模糊神经网络的粒子群优化优化算法设计

模糊理论和神经网络算法是目前应用较广两种融合算法，本文综合两种算法的优势，采用模糊系统和BP神经网络组合的自适应模糊神经网络对异构数据的融合。基于BP神经网络构成的自适应模糊神经网络，其模糊规则满足：

针对模糊神经网络参数学习对融合速度和精度的限制，本文设计一种粒子群学习算法来优化异构导航数据融合指标。粒子群学习算法如下：

假设在n维空间中，种群规模为m的粒子群X为

按照追随当前最优粒子原理，第i个粒子在第j个维度空间中的速度与位置分别满足

全局误差为

其中，pij为个体极值；pgj为全局极值；t为进化代数；r1和r2为随机数，取值范围满足[0,1]区间；c1和c2为加速常量。

该优化算法通过调节全局最优粒子和个体最优粒子飞行的最大步长，使得全局误差最小，即保证粒子快速趋向全局最优。

3 基于模糊神经网络的粒子群优化优化算法仿真分析

选用3种异构导航数据，分别作为目标的距离、速度和角度，在目标运动的30s内选择100组数据进行仿真分析。目标的初始距离为(3500，4000)，初始速度为(25，0.1)，初始角设为30°。新算法下，导航数据的融合误差仿真结果如图2所示。

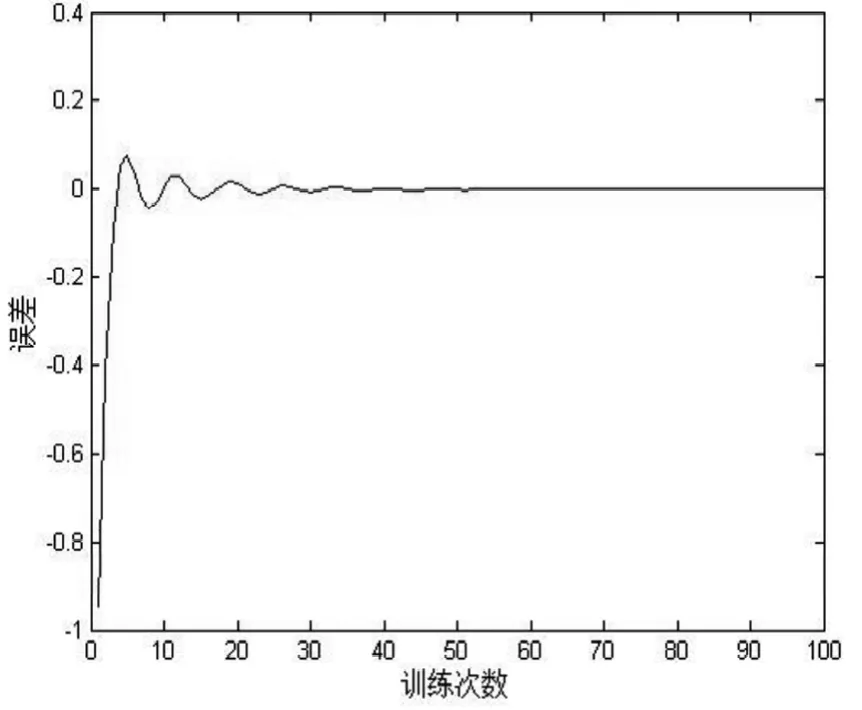
图2：导航数据的融合误差

图3：粒子群算法最优个体适应度

由图2可以看出，在100次的粒子群参数学习中，随着学习次数的增加，误差逐渐趋于平缓，融合误差的方差约为0.51，可有效实现对导航数据的聚类融合。由图3可以看出，新算法寻优在12次迭代后可满足最优个体适应度，即搜索到空间最优个体。综合可知，新算法可降低融合误差，提高融合精度，减小学习迭代次数，增加收敛速度，满足导航数据的实时性，提升对导航目标的动态预测能力。

4 结论

为有效提高导航数据的融合精度和融合速度，本文基于自适应模糊神经网络设计了一种粒子群优化算法，并对该算法进行仿真验证。结果表明，新算法能够有效降低数据融合误差，提高参数学习速度，新算法适合在动态、多目标环境中快速寻优。