促进优化思想生长的教学策略
姚辛酉
解决问题能力的培养是义务教育阶段数学课程的重要目标之一。有些问题的解决会出现多种策略,通过猜想、验证等找出最合理、最省时、最优的策略就是优化。在这个过程中形成的思考路径、操作方法、解题策略就是优化思想的体现。教师应注重引领学生经历优化的过程,感受优化思想的价值。
一、生长源于对问题本质的理解
在解决问题前,教师首先要引导学生认真读题,找出题目所给的条件和要求的问题,在此基础上仔细挖掘,找出问题的本质。这一过程是优化思想的生长之源。
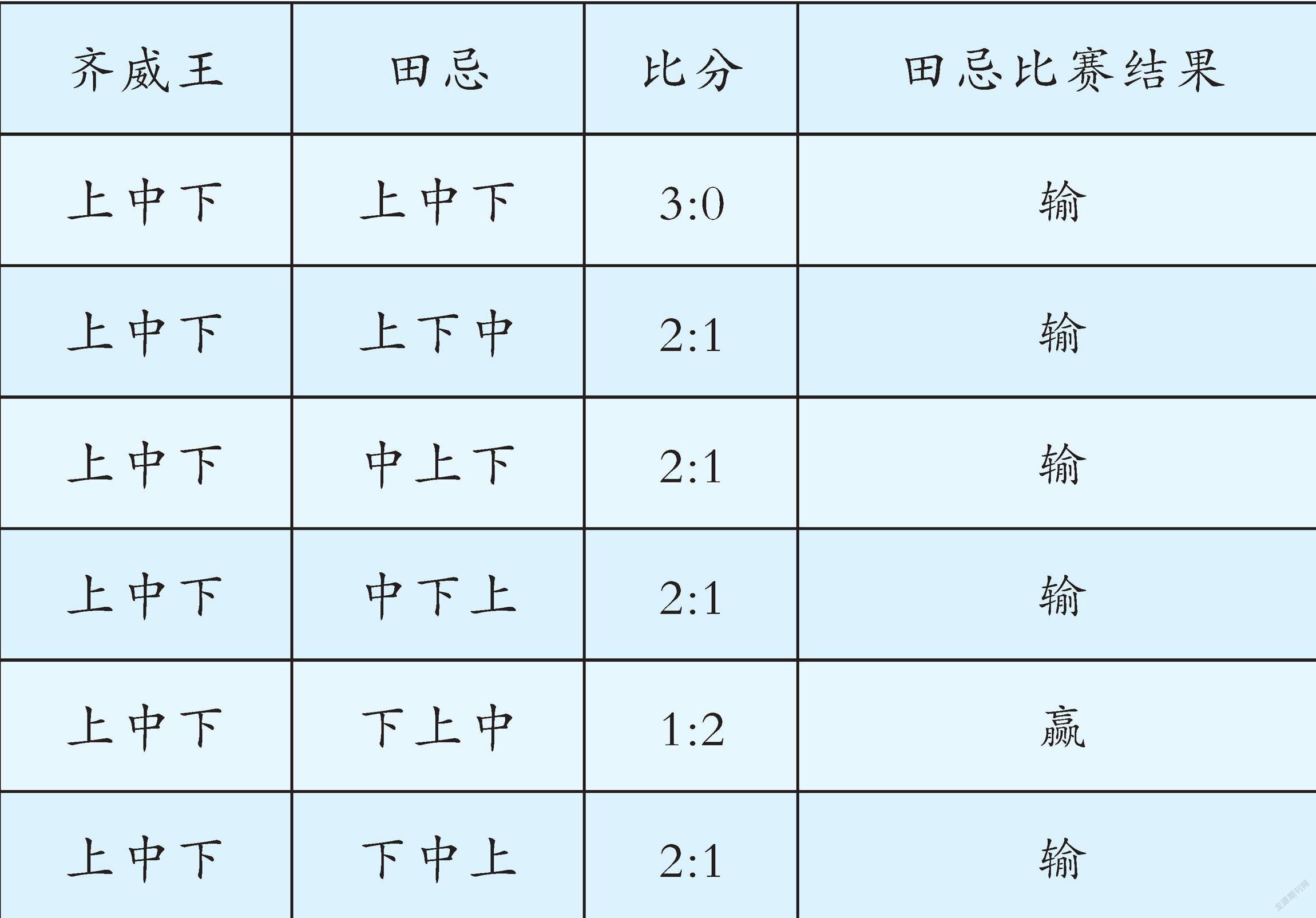
在学习“田忌赛马”时,笔者首先引导学生对已知条件进行梳理,得出初步结论——所有条件都对田忌不利。由于对阵方案较多,笔者让学生采用列表法,将所有方案一一列举出来(如下表),再进行具体分析。
观察表格,我们可以发现:田忌和齐威王赛马,在齐威王对阵方式不变的情况下,田忌有6种应对方式。在这6种方式中,只有1种能够获胜。因此,解决“田忌赛马”问题的关键,就是把所有可能性逐一列举出来,并从中找出唯一的获胜策略。
二、生长源于对问题的深度思考
学过“田忌赛马”这节课,学生应该获得如下经验:遇到一个问题首先应该从总体上进行把握,列举出各种可能性,选出最优的一种,再从中找出具体的解决方案。这一过程是优化思想的生长之根。
通常,学生对“田忌赛马”问题的认知都会经历“不可能赢—有可能赢—思考为什么可能赢”的过程。初读问题,学生按照常规的对阵策略思考,会认为由于田忌每一档次的马都比齐威王的差一些,三局一定都会失败,田忌获得胜利的可能性几乎为零。这是学生经历的第一个认知阶段。随后,笔者引导学生继续思考:“像刚才那样,分别安排上等马、中等马、下等马对阵,就叫作策略。很明显,解决这个问题不止一种策略,大家可以试一试其他策略。”学生思考后回答:“用田忌的下等马对阵齐威王的上等马,用田忌的上等马对阵齐威王的中等马,用田忌的中等马对阵齐威王的下等马。”笔者追问:“这样的对阵策略有什么好处?”学生回答:“这样对阵,虽然第一局会输,但是后面两局会赢。”学生经历了调整对阵顺序的过程,思维进一步发散。以上是学生经历的第二个认知阶段。为了让学生明确田忌可能获胜的原因,笔者引导学生观察上文提到的表格中6种策略的比分情况,并说一说有什么发现。一名学生说:“要想获得胜利,比分只能是2∶1。”另一名学生说:“想要以3∶0的比分获胜是不可能的。”笔者追问为什么不可能取得3∶0的比分。学生回答:“因为田忌每一档次的马都比齐威王的要差一些,田忌派什么马都比不过齐威王的上等马,因此这一局只能输。”还有的学生回答:“因为第一局输了,后两局就必须要赢,总比分才能是2∶1,而田忌用上等马对阵齐威王的中等马、用中等马对阵齐威王的下等马就可能获胜两局。”这样教学,使学生建立起从总体到局部的思考路径。这是学生经历的第三个认知阶段。
三、生长源于对问题的类比与延伸
“田忌赛马”问题不仅仅是赛马问题,本质上是融会了众多策略的博弈问题。在这些问题中,有的要从条件入手分析,找出最优方案;有的无法从条件入手,只能根据问题进行倒推;还有的必须跳出题目从整体上进行思考。基于此,笔者设计了不同类型的练习,引导学生在解决问题的过程中提升优化思维。
教材课后习题设置了两人玩扑克牌比大小的游戏。红色的一组扑克牌牌面数字分别是5、7、9,黑色的一组扑克牌牌面数字分别是3、6、8,两人各持一组牌,每人每次出一张牌,各出3次,赢2次者胜。问题是持黑色扑克牌的人是否有可能获胜。学生在解答这道题时,很容易与“田忌赛马”问题产生类比,通过迁移得到:红色扑克牌“9”相當于齐威王的上等马,“7”相当于中等马,“5”相当于下等马;黑色扑克牌“8”相当于田忌的上等马,“6”相当于中等马,“3”相当于下等马。如果按相同档次的牌面数字对阵,持黑色扑克牌者一定会输。由此得出,当对方出“9”的时候,自己应出“3”;对方出“7”的时候,自己出“8”;对方出“5”的时候,自己出“6”,这样可以获得两胜一负,取得最终胜利。此题是对所学内容的基本练习。
在此基础上,笔者拓展题目类型,出示如下练习:“100根粉笔,两人轮流取,每人每次最少取1根、最多取10根,谁能取到最后剩下的粉笔,谁就是胜者。问:先取者为了战胜对手,第一次应取几根粉笔?”解决此题的关键是抓住“最多取10根”,先取者只要到最后一次给后取者剩下11根,无论后取者取多少根,最后的赢家一定是先取者。因此,先取者第一次取后留下的根数是11的倍数即可。所以先取者为了战胜后取者,第一次应取1根粉笔。这一题虽然还是对阵问题,但与“田忌赛马”问题有较大区别。“田忌赛马”中,齐威王的对阵策略是固定的,因此只需要针对一种情况来制订应对策略,而本题由于对阵时对方有多种策略,而应对的办法各有不同,因此无法从条件入手分析,只能从结果入手分析。
笔者再出示不同类型的题目:有25个人在一起围成一个圆圈,从某人开始,按1、2、3……的顺序报数,第一次去掉报奇数的人,去掉之后再次报数,再去掉报奇数的人,如此反复下去,最后剩下的人是原来的几号?笔者引导学生画图分析,这道题第一次去掉的是报奇数的人,剩下的都是报偶数的人;第二次去掉的是原来报的数里面只含有一个因数2的人;第三次去掉的是原来报的数里只含有两个因数2的人……按照这样的规律,哪一个数中含有的因数2最多,那一个数就是最后剩下的人的序号。25以内含有因数2最多的数为16,所以剩下的人就是原来报的数为“16”的人。
四、生长源于对问题的一般归纳
结课时,笔者引导学生回顾研究问题的过程,并提问学生“有什么收获”。学生反馈:“调换马匹的出赛顺序可以获得胜利”“取粉笔的题目告诉我们,可以从结果进行思考”“可以用画图的方法来解决比较难的问题”。笔者将其总结为“调换顺序”“逆向思考”“画图解题”等思考策略。
整节课的教学,教师注重引导学生经历知识建构的完整过程,让学生在挖掘问题本质的基础上进行深度思考,得出初步结论,之后通过发散练习,获得进一步的提升,最终总结出解决这一类问题的方法,形成优化的数学思想,促进了学生思维能力的整体提升。
(作者单位:孝感市实验小学)

