高地应力下岩体爆破数值模拟分析

郭云龙 孙崔源 康永全 孟海利 薛里

（中国铁道科学研究院集团有限公司铁道建筑研究所，北京100081）

由于我国经济建设需要，在高原地区修建铁路隧道已在所难免。高地应力的存在对传统隧道爆破开挖技术提出了挑战。众多学者对高地应力作用下岩体爆破技术进行了研究。在爆破机理方面，张西良等［1］对不同围岩压力下岩体爆破进行了数值模拟，得到岩体爆破损伤范围随围岩压力增大而缩小，高围岩压力对岩体拉伸破坏的抑制效果更明显。杨建华等［2］分析得出地应力增大会导致更多炸药爆炸能量转化为地震波能量，较高水平的地应力对爆区破碎范围的发展有抑制作用。李新平等［3］对不同地应力下掏槽孔爆破进行了数值模拟，得到初始地应力对掏槽孔爆破有抑制作用，爆破面会朝着相对较大的地应力方向发展。李莹［4］利用显式动力学软件LS-DYNA对不同初始地应力状态下岩体爆破过程进行了数值模拟，发现初始地应力场与爆炸应力波叠加对岩体破坏影响很大，初始地应力的存在抑制了裂隙区和爆破漏斗的发展。在爆破卸压技术方面，杨永良等［5］认为爆破卸压法的实质是在炮孔底部集中装药爆破，使洞周附近的围岩与深部岩体脱离，将应力向岩体深部转移，并通过工程实例验证了卸压爆破的可行性。谢勇谋等［6］研究得出当岩石内聚集的应力接近强度极限时，爆破具有诱发岩爆的作用；当岩石内应力远低于强度极限时，爆破对岩爆的产生具有控制性作用。陈萍萍［7］研究得出最佳爆破卸压方案是炮孔爆破使巷道轴线方向、横断面方向围岩爆破损伤范围均贯通。

本文对垂直炮孔方向和平行炮孔方向2个方向的初始地应力共同作用下岩体爆破效果和爆炸应力波传播规律进行研究。

1 高地应力作用下破岩机理

大量试验证明，岩体受到的围岩压力随埋深增加而增大。岩体所处地应力与埋深并非简单线性关系。地应力大小与该处岩体走向、地质构造、岩质类型等密切相关。深埋岩体爆破破碎是由爆破动荷载和地应力静荷载共同作用所致［8］。与浅埋岩体爆破不同，深埋岩体初始地应力较大，随着初始地应力增加，岩体所受约束增大，内部缝隙在高围岩压力作用下压紧致密，进一步限制了岩体变形发展，岩体极限承载力显著提高。在深埋岩体中钻孔爆破时，随着围岩压力增加爆破空腔缩小，裂缝扩展受阻，爆破难度提升，破岩效果变差，单位体积破碎将消耗更多炸药量。

2 有限元数值模拟

2.1 模型的建立

为节省计算时间，建立z方向单层实体单元网格模型（图1）。为确保计算精度，尽可能缩小网格尺寸。计算模型尺寸为1.0 m（x方向）×1.0 m（y方向）×1.25 mm（z方向），装药直径32 mm，填塞直径42 mm，采用耦合装药结构，装药长度225 mm，填塞长度400 mm。计算模型包含255 924个节点，126 692个实体单元。炮孔位于模型中间，设定炸药从孔底中心起爆。空气域覆盖整个岩体模型。

图1 计算模型及监测点布置（单位：m）

对整个模型施加z方向位移约束，对岩体模型的底部施加y方向位移约束，周边施加x方向水平地应力σx（垂直炮孔方向），顶部施加y方向竖直地应力σy（平行炮孔方向）。整个模型四周设置无反射边界，以吸收入射波，防止对计算结果产生干扰。

布置爆炸应力波监测点，测点间距10 cm，其中测点1距离炮孔中心线10 cm。

计算分为2步：①利用有限元软件隐式求解功能对岩体进行应力初始化；②将计算得到的岩体单元网格节点的受力、位移等数据导入到动力计算模型中，通过显式求解功能完成爆炸动荷载计算。

2.2 材料参数的选取

计算模型由炸药、空气、填塞物和岩体组成。炸药和空气网格采用任意拉格朗日-欧拉（Arbitrary Lagrange-Euler，ALE）算法，均设置为多物质单元。填塞物和岩体网格采用拉格朗日算法。填塞物与岩体之间采用面面接触。为了防止单元网格畸变导致计算困难或终止，采用流固耦合算法处理单元之间的相互作用关系。

炸药爆炸产生动荷载，利用软件提供的高能炸药模型，通过JWL（Jones-Wilkins-Lee）状态方程［9］描述炸药体积和压力之间的关系，并精确表达爆炸动荷载。

JWL状态方程为

式中：P为炸药爆炸产生的压力；A，B，R1，R2和ω均为与材料相关的常数；V为炸药的相对体积；E0为炸药的初始内能密度。

炸药参数见表1。

表1 炸药参数

空气采用空材料模型，密度为0.125×10-2g/cm3。填塞物采用双线性弹塑性材料本构模型。填塞物力学参数见表2。

表2 填塞物力学参数

有限元软件提供了2种模拟爆破损伤方法：①通过单元失效关键字定义岩体抗压和抗拉强度极限，当岩体单元所受应力超过极限值时将自动失效删除，可形象模拟裂缝扩展；②将岩体单元设置为具有损伤功能的材料本构模型，计算结果更为准确。针对不同分析，2种方法本文均有采用。

岩体采用Holmquist，Johnson和Cook提出的HJC本构模型［10］和方法①定义单元失效准则，模拟岩体爆破裂缝扩展，清晰展现不同初始地应力下岩体爆破损伤情况。依据方法②岩体材料采用RHT（Riedel-Hiermaier-Thoma）损伤本构模型［11］，研究不同初始地应力对爆炸应力波传播规律的影响。岩体材料主要物理力学参数见表3。

表3 岩体材料主要物理力学参数

2.3 计算工况

为研究不同初始地应力下岩体爆破裂缝扩展情况及爆炸应力波传播规律，其他参数保持不变，只改变初始地应力。考虑到地应力相对复杂，只关注σx和σy。σx和σy均分别取0，20，40 MPa。研究侧压力系数λ（σx/σy）的影响时，保持σy为20 MPa，σx从20 MPa逐渐增至70 MPa，每次增量为10 MPa。计算工况见表4。爆破模拟计算时间为3 ms。

表4 计算工况

2.4 模拟结果与分析

2.4.1 初始地应力对岩体爆破损伤的影响

σx与σy大小相等时，工况1—工况3爆破1.5 ms时岩体损伤情况见图2。可以看出，不同工况下岩体爆破损伤范围不同。工况1爆破动荷载超过岩体极限抗压强度，岩体沿炮孔方向产生空腔。远离炮孔一定距离，爆破应力波逐渐衰减，岩体所受爆破应力低于其极限抗压强度，岩体中衍生出的动拉应力高于岩体极限抗拉强度，炮孔四周出现辐射状爆破裂缝。

图2 不同工况爆破1.5 ms时岩体损伤情况

保持σy为20 MPa不变，改变σx大小（工况2、工况4—工况8），不同侧压力系数下爆破1.5 ms时岩体损伤情况见图3。不同工况爆破前后岩体体积及爆破损伤率见表5。

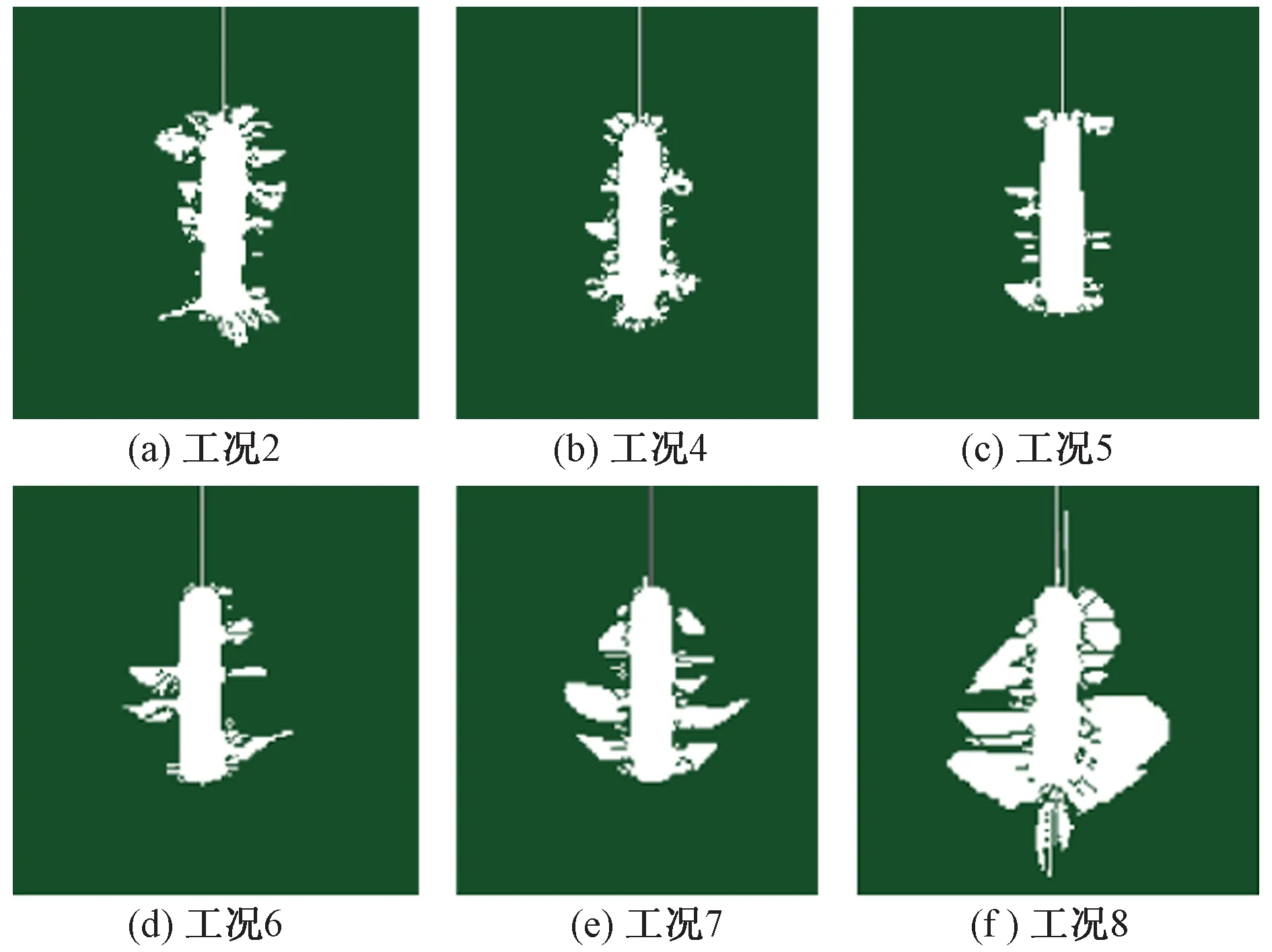
图3 不同工况爆破1.5 ms时岩体损伤情况

表5 不同工况爆破前后岩体体积及爆破损伤率

由图3和表5可知：①σy为20 MPa，不同侧压力系数下岩体爆破损伤范围不同。侧压力系数由1.0逐渐增至2.0时，岩体爆破损伤率（爆破后岩体体积/爆破前岩体体积）由2.169%逐渐降至1.767%；侧压力系数由2.0增至3.5时，岩体爆破损伤率由1.767%增至7.958%。说明当侧压力系数达到一定值时，初始地应力对岩体爆破损伤范围的抑制作用达到最大；当侧压力系数继续增大，岩体爆破损伤范围增大，损伤沿垂直炮孔的较大初始地应力方向扩展。故高地应力区进行岩体爆破时，应尽量让炮孔方向垂直最大地应力。②工况1—工况3初始地应力σx与σy大小相等，两者从0增至40 MPa时岩体爆破损伤范围越来越小。从0增至20 MPa时岩体爆破损伤率降低了6.422%；从20 MPa增至40 MPa时岩体爆破损伤率降低了0.642%。说明平行炮孔方向和垂直炮孔方向初始地应力相等时，初始地应力越大，岩体爆破损伤范围越小，爆破效果越差。

2.4.2 初始地应力对爆破应力波传播的影响

工况1—工况3各测点的爆破应力波传播规律相同。测点3的爆破应力时程曲线见图4。可知：①工况下1—工况3测点3爆破应力波的初始值分别为0，18.1，37.6 MPa，说明σx与σy越大，测点初始爆破应力越大。不同工况下测点3爆破应力时程曲线变化规律相同，爆破动荷载作用时长一致，爆后各自恢复到之前的地应力水平。②工况1—工况3测点3在爆破0.68～0.69 ms时爆破应力峰值分别为97，114，124 MPa。说明测点3爆破应力峰值随着初始地应力增大而增大。

图4 不同工况测点3爆破应力时程曲线

工况1—工况3各测点爆破应力峰值曲线见图5。可知，同一工况下随着测点与炮孔距离增大，爆破应力波逐渐衰减，爆破应力峰值逐渐减小。

图5 不同工况各测点爆破应力峰值曲线

σy为20 MPa时，不同侧压力系数下各测点爆破应力峰值见表6。侧压力系数由1.0增至1.5时测点1爆破应力峰值稍有增大，测点2和测点3爆破应力峰值均减小；侧压力系数由1.5增至3.5时各测点爆破应力峰值均逐渐增长，有利于改善岩体爆破效果。

表6 不同侧压力系数下各测点爆炸应力峰值 MPa

3 结论

1）平行和垂直炮孔方向的初始地应力相等时，初始地应力越大，爆破损伤率越低，爆破效果越差。

2）侧压力系数对炮孔爆破损伤范围有影响，随着侧压力系数逐渐增大，损伤范围先减小后增大。在爆破损伤范围增大过程中，损伤沿垂直炮孔的较大初始地应力方向扩展，故在高地应力区进行岩体爆破时应尽量让炮孔方向垂直最大初始地应力，以提升爆破效果。