基于改进模糊C均值聚类和区域合并的矿物颗粒分割方法

朱 磊，滕奇志*，龚 剑

(1.四川大学电子信息学院图像信息研究所，成都 610065； 2.成都西图科技有限公司，成都 610024)

在石油地质部门的岩矿石薄片自动化分析鉴定工作[1]中，图像处理技术的应用越来越深入，矿物颗粒的自动化分割提取是整个分析鉴定工作的首要任务，分割提取结果的好坏直接影响了矿物分类、粒度分析等后续步骤。由于矿物颗粒之间的边缘较为模糊，且纹理比较复杂，在一幅单偏光图像上应用传统的图像分割算法难以将颗粒完整地提取出来，笔者研究团队研制了一种正交偏光图像[2]采集设备，能够获得薄片不同角度的正交偏光序列图像，通过序列图像，具有消光性[3]的矿物颗粒有较好的区分度，在此基础上讨论了多种颗粒分割算法。文献[4]提出一种基于统计区域合并(statistical region merging，SRM)的岩矿石颗粒分割方法，相较于传统的单幅单偏光图像分割算法，该方法根据岩矿石颗粒在一组正交偏光序列图像下的特征进行分割提取操作，提高了分割效果，改善了颗粒的欠分割现象，然而，该方法采用传统的多阈值分割算法[5]进行初始的分割，对于矿物颗粒之间差异明显，结构简单的岩矿石薄片图像，采用多阈值分割算法可以满足需要，但对于其他组分复杂、填隙物众多的薄片图像，多阈值分割算法的分割效果不够理想，因而也影响了后续的合并操作，致使最终结果不够理想。文献[6]提出一种基于边缘流的颗粒分割算法，该方法可以有效提取出大部分的矿物颗粒，但由于边缘流算法对边缘信息过于敏感，致使某些表面粗糙的矿物颗粒产生过分割现象，同时也容易导致一定的误分割现象。文献[7]采用一种先分割后合并的策略进行颗粒提取，但采用的合并准则只考虑了图像的颜色和亮度信息，导致某些过分割区域不能正确合并，且采用的合并算法过于简单，合并效率偏低。为了解决上述算法的问题，提出一种新的基于正交偏光序列图的分割算法。

模糊C均值聚类(fuzzyC-means，FCM)是一种基于模糊理论的分类算法，实现简单，效率高，分割效果好，并且可以实现无监督分类，在图像分割领域的运用越来越广泛。针对岩矿石薄片图像中的矿物颗粒种类繁多，且不同薄片图像之间的差异可能会比较大的特点，现采用适合于矿物颗粒分割的FCM算法进行初始的边缘提取。但由于传统的FCM需要人工确定聚类数目，且初始聚类中心是随机选择的，容易导致运行时间过长、分割结果不理想、多次运行结果不相同等后果。现提出一种改进的FCM算法，可以自适应地确定聚类数目和初始聚类中心点。对每一张正交偏光序列图运用该方法进行初始的边缘提取并叠加得到的边缘图像，然后对叠加边缘图像进行精细化处理以及颗粒筛选，针对多张边缘图像叠加导致的过分割现象，提出一种结合颜色、纹理、亮度等多维度信息的合并准则，并利用基于区域邻接图(region adjacency graph，RAG)的合并算法进行区域合并操作。实验结果表明，通过叠加多张边缘结果图，可以精确定位矿物颗粒的边缘，后续的合并操作也能有效处理过分割现象，并且合并效率也得到了很大的提高。

1 基于正交偏光序列图的改进FCM算法

1.1 FCM算法

FCM算法[8]是一种基于划分的无监督分类算法，它将图像的每个像素点划分到不同的类别中，使相同类别像素之间的差别最小，不同类别像素之间的差别最大。普通C均值算法明确规定每个样本必然属于某一类，模糊C均值算法则是利用隶属度函数指出某个样本属于某个类别的程度，隶属度函数取值范围为[0，1],若取值为1，则表示该样本必然属于该类别，若取值为0，则表示该样本必然不属于该类别。FCM算法一般由以下步骤组成。

步骤一确定聚类数目c，最大迭代次数Ep，迭代中止误差Mi以及参数m，并初始化聚类中心pj。

步骤二设uij为第i个样本属于第j类的隶属度，dij为第i个样本与第j类聚类中心之间的距离，按照式(1)更新隶属度函数。

(1)

步骤三设第j个聚类中心为pj，一共有n个样本点，xi表示第i个样本点，按照式(2)更新聚类中心。

(2)

步骤四设目标函数为q，按照式(3)计算目标函数。

(3)

步骤五若达到最大迭代次数或者是前后两次目标函数的绝对值差小于迭代停止误差时，中止迭代，并将每个样本划分到其隶属度函数最大的类别。

1.2 聚类数目和初始聚类中心点的确定

原始的FCM算法需要人工确定聚类数目，如果聚类数目过少，会丢失图像很多的细节，如果聚类数目过多，又会带来很多不必要的信息。而且原始FCM算法的初始聚类中心点是随机选择的，如果选择的初始聚类中心不合理，很容易导致算法运行时间过长，且易陷入局部收敛状态，使得聚类结果不理想。提出一种初始化算法，可以自动确定聚类数目并选择初始聚类中心，显著减少了算法的运行时间,提高了算法的分割精度。

根据图像的RGB(red green blue)颜色信息进行聚类，其中红(R)、绿(G)、蓝(B)范围为0～255，在此基础上确定聚类数目和选择初始聚类中心。具体步骤如下。

步骤一将R、G、B每个通道的256个特征值分类，值为[0,16)属于第一类，值为[16,32)属于第二类，值为[32,48)属于第三类，以此类推，每个通道分为16类。

步骤二将每一个像素点分类，当且仅当两个像素点的每个通道都属于同一类时，这两个像素点归为一类，一共有16×16×16类，计算每一类的像素点数目，并根据像素点数目的多少对类别排序。

步骤三初始化聚类中心列表为空列表。依次取像素点数目最多的类别，计算该类别所有像素点的R、G、B均值，作为一个聚类中心加入聚类中心列表，如果聚类中心列表中某一个聚类中心与该类别计算出的聚类中心的欧式距离小于50时，取消加入。

步骤四遍历完所有类别之后，初始化聚类中心列表中的每个元素即为所有的初始化聚类中心，列表的元素数即为聚类数目。

1.3 基于正交偏光序列图的改进FCM算法

岩石矿物薄片种类繁多，成分复杂。主要研究对象为砂岩薄片，薄片中常见的颗粒类型有石英、碱性长石、斜长石[9]等，不同的颗粒在颜色、纹理等方面都具有不同的特征，如图1所示，在普通单偏光显微镜下拍摄的单偏光岩矿石薄片图像中，矿物颗粒的边界模糊，直接在普通单偏光图像上运用分割算法很难得到良好的分割提取结果。

图1 单偏光图像Fig.1 Single polarized image

图2 正交偏光序列图Fig.2 Orthogonal polarized sequence images

很多矿物颗粒在正交偏光下会表现出消光性，具有较好的区分度，在正交偏光序列图像上运用分割算法可以取得更好的效果。图2是在0°～160°区间内，每隔20°采集一张正交偏光图像所得的一组正交偏光序列图。由于矿物颗粒的消光性，单独一张正交偏光图像并不能反映该视域内的所有矿物颗粒信息，所以需要整合每一张正交偏光序列图的信息。取每一个像素点作为FCM聚类的样本数据，样本与样本之间的距离取对应像素点每个通道之间的欧式距离，使用改进FCM算法对每一张正交偏光序列图进行聚类，并取聚类结果的边缘，图3是对每张正交偏光序列图像运用改进FCM算法并取边缘的结果。

通过对每张边缘结果图进行简单的叠加操作，可以得到图4所示的一张叠加边缘图像。可以看到，由于多张正交偏光序列图提取到的边缘信息过于丰富，叠加边缘图像显得非常粗糙杂乱，需要对叠加边缘图像进行精细化操作，具体步骤如下。

图3 边缘结果图Fig.3 Edge result images

(1)对叠加边缘图像进行形态学操作，先膨胀，再腐蚀，可以去除整合大部分重合的边缘。

(2)进行骨架化操作，可以去除叠加边缘图像大部分的细枝末节。

(3)最后进行膨胀操作。图5展示了精细化边缘结果图。

图4 叠加边缘结果图Fig.4 Result image with superimposed edges

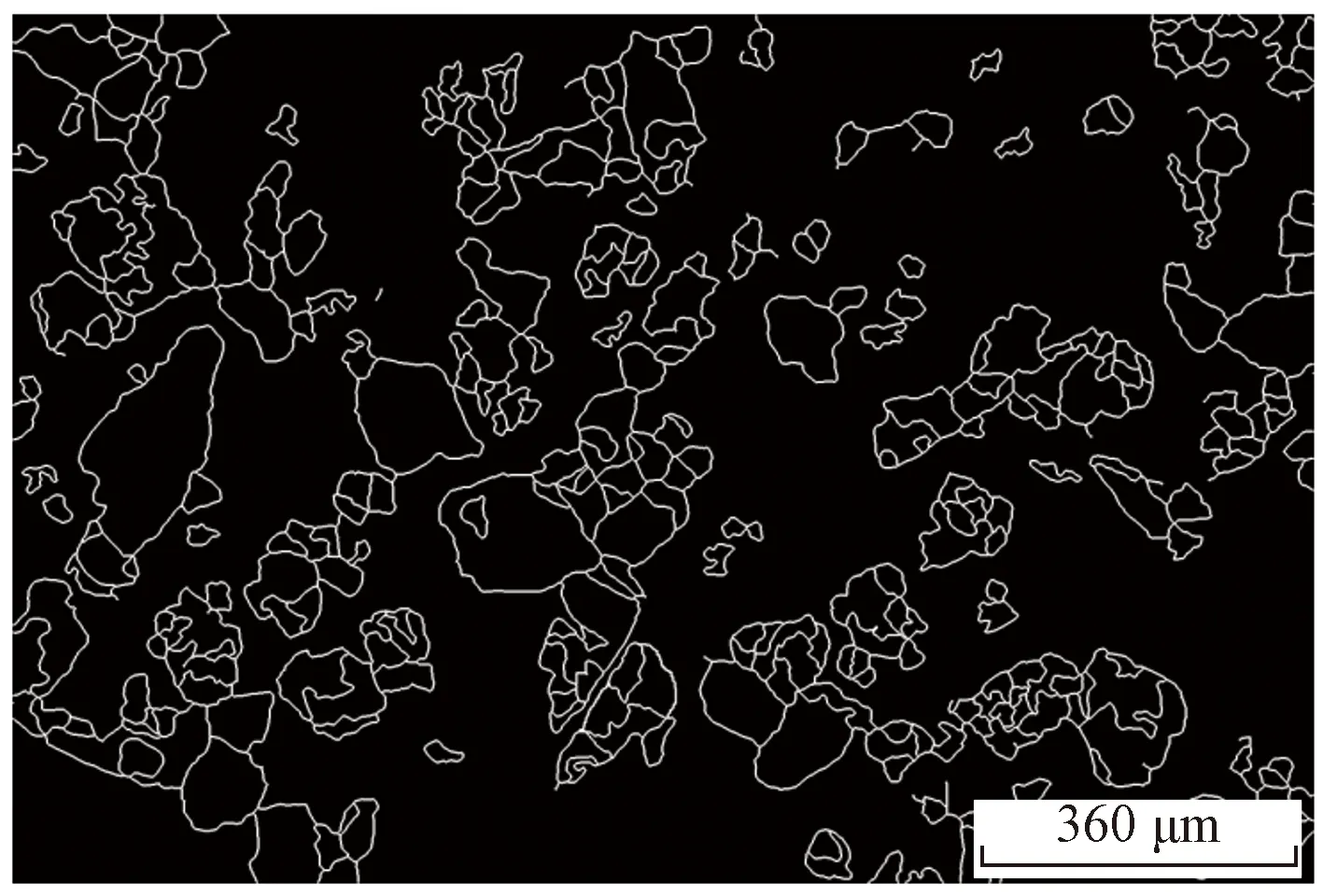
图5 精细化边缘结果图Fig.5 Result image with refined edges

对得到的精细化边缘结果图取反，并计算每个分割区域在序列图中的最大亮度均值Imax，将Imax小于阈值It的目标区域设为背景，进而筛选出目标颗粒，通过大量的实验表明，It取30可以得到最好的效果。图6为目标颗粒筛选后的结果图。

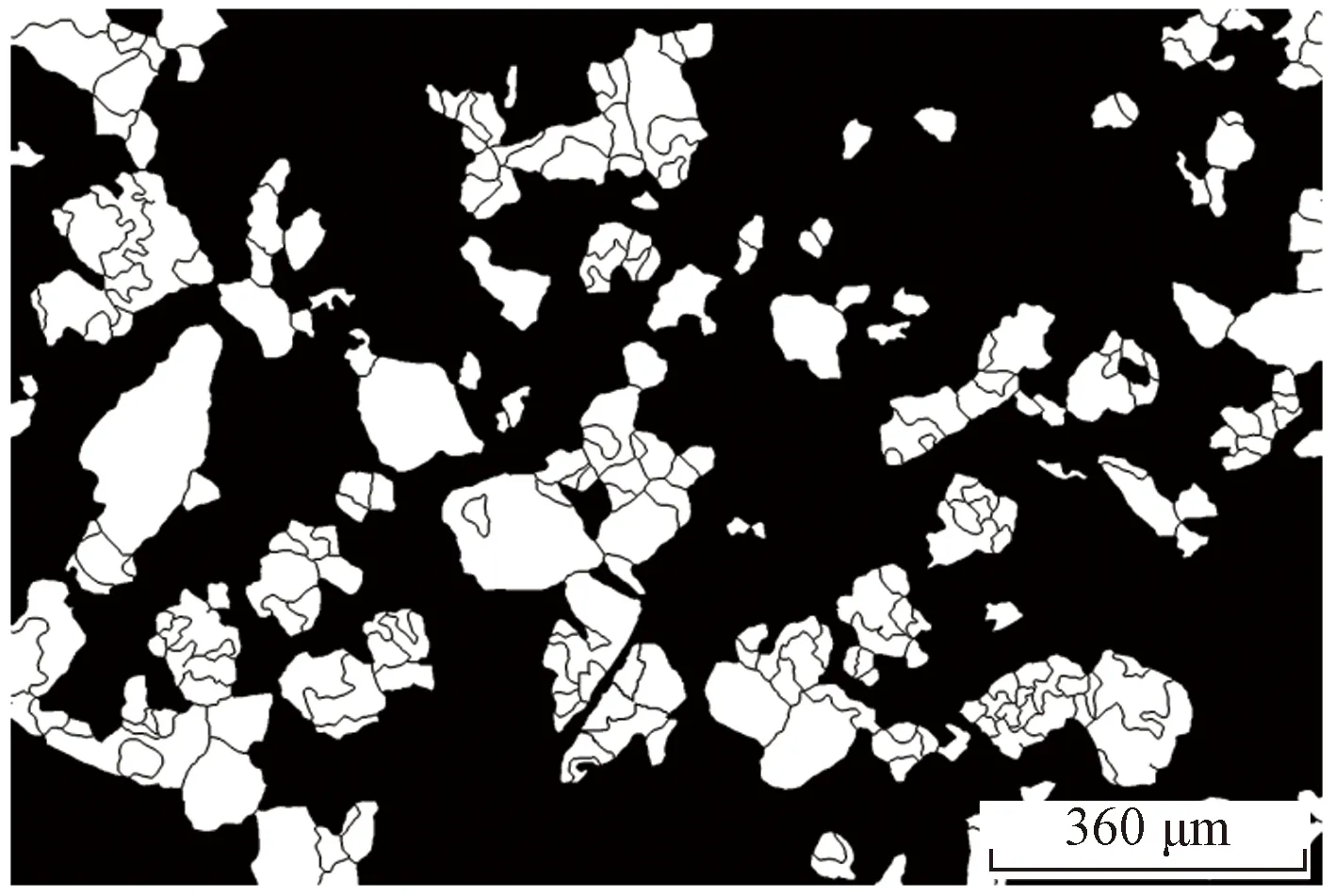
图6 目标颗粒筛选结果图Fig.6 Result image with filtered target particles

2 基于颜色纹理信息的合并操作

上文所述的岩矿石颗粒在正交偏光下表现出消光性，有较好的区分度，通过正交偏光序列图能够更容易提取到矿物颗粒的边缘信息，但由于矿物颗粒复杂的纹理特征[10]以及某些噪点的影响，同一个矿物颗粒内部难免呈现出消光程度不一致的现象，这就会造成误分割，除此此外，多张边缘图像的叠加，也会加剧误分割，最终造成明显的过分割现象。如图6可以看到明显的过分割现象，为了有效抑制过分割，采用基于RAG数据结构的合并算法根据矿物颗粒的颜色、纹理以及在不同正交偏光角度下的变化规律进行区域合并操作。

2.1 基于颜色信息的合并准则

单独一张正交偏光图像并不能反映该视域内的所有矿物颗粒信息，对图2所示的九张正交偏光序列图像按照式(4)进行差分融合操作，其中g(x,y)为融合图像，gR(x,y)、gG(x,y)、gB(x,y)分别为融合图像R、G、B三个分量的值，giR(x,y)、giG(x,y)、giB(x,y)分别为第i张正交偏光序列图R、G、B三个分量的值。如图7所示，融合图像基本涵盖了视域中所有颗粒的信息。第2节的合并操作均基于此融合图像。

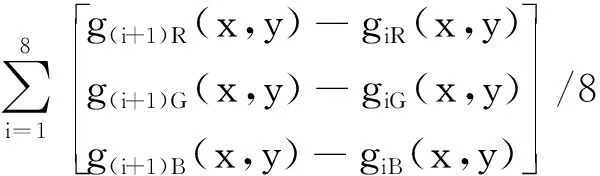
(4)

图7 融合图像Fig.7 Fused image

在统计学中，卡方检验[11]可以统计样本的实际值与理论值之间的偏差，实际值与理论值之间的偏差越大，卡方检验得到的值越大，实际值与理论值之间的偏差越小，卡方检验得到的值越小。卡方检验的计算公式为

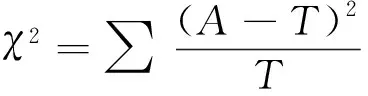
(5)

式(5)中：A为实际值；T为理论值；χ2为卡方值。

卡方比较源自卡方检验，用于测量比较两组样本的相似性程度，当卡方比较值越大时，相似性程度越低，当卡方比较越小时，相似性程度越高，卡方比较在进行直方图的相似性度量中表现出良好的效果。假设两直方图分布分别为h1和h2，卡方为d(h1,h2)，卡方比较公式为

(6)

采用卡方比较来衡量两个颜色直方图的相似程度，定义颜色相似度RErgb(X,Y)为

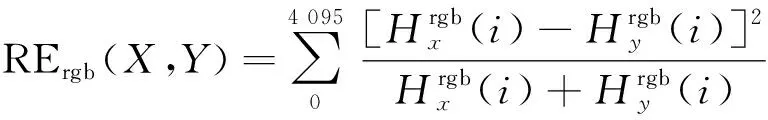
(7)

可知RErgb(X,Y)越小，相邻两目标区域相似性越大。

2.2 基于纹理信息的合并准则

同一种矿物颗粒在纹理上也具有相似性，例如石英颗粒表面纹理比较光滑，而碱性长石表面比较粗糙，斜长石表面具有条形纹理等。利用局部二值模式(local binary pattern,LBP)算子对具有相似纹理特征的颗粒目标区域进行合并。

LBP是一种用来提取纹理特征的算子[12-13]，在一个3×3的窗口中，以中心像素点的像素作为阈值，周围正方形八领域的像素与之进行比较，若大于中心像素点的像素则将其置为1，反之则置为0。由此得到一个八位的二进制LBP码,此二进制LBP码反映了这个区域的纹理特征。

上述LBP算子计算的区域只覆盖了3×3的区域范围，面积很小，不能满足提取不同尺寸纹理特征的需求。文献[14]对LBP 算子进行了改进，将上述正方形邻域扩展到了圆形邻域，并允许圆形邻域的半径为任意长度，设(R,P)表示半径为R并且有P个邻接像素点的圆形邻域，图8展示了选择的(2,8)圆形邻域示意图。同样将周围圆形邻域的每个像素与中心点的像素进行比较，若大于中心点的像素则将其置为1，反之则置为0，由此得到一个八位的二进制码，该二进制码一共有28种不同的模式。通过旋转(2,8)的圆形邻域，可以得到不同的二进制码，为了减少二进制码的模式种类，选择最小的二进制码作为该区域的纹理特征[15]，总的模式种类数降为28/8=32种。大多数计算出的二进制码最多包含两次0到1或1到0的跳变[16]。为了进一步减少二进制码的模式种类，将跳变次数大于两次的二进制码归为同一类，则模式种类进一步减少到10种。

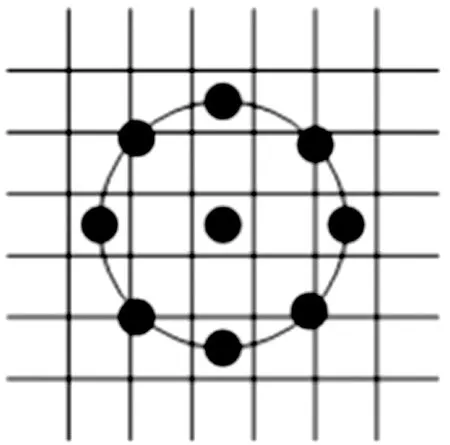
图8 (2,8)圆形邻域Fig.8 (2,8)Circular neighborhood

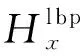
(8)

RElbp(X,Y)越小，相邻两目标区域相似性越大。综合颜色相似度和纹理相似度对相邻两目标区域是否属于同一区域进行判断，定义综合相似度RE(X,Y)为

RE(X,Y)=0.5RErgb(X,Y)+0.5RElbp(X,Y)

(9)

2.3 基于RAG的区域合并算法

RAG是一种描述图中每个区域邻接关系的数据结构[17]，本质上是一种无向加权图。过分割结果图中的每个区域对应RAG中的一个节点，相邻的两个过分割区域之间的邻接关系对应RAG中的一条边，表示这两个区域相互邻接，且这两个区域之间的相似度对应这条边的权值，图9是将过分割结果映射为RAG的示意图。基于RAG的区域合并算法的步骤如下。

步骤一根据目标颗粒筛选结果图初始化RAG数据结构，建立对应节点及边，并根据指定的合并准则确定每条边的权值，采用如式(9)所示的综合相似度作为合并准则。

步骤二寻找具有最大权值的边，合并其连接的两个节点，即合并对应的两个相邻目标区域。

步骤三重新计算新节点的相似度信息，并更新邻接边的权值。

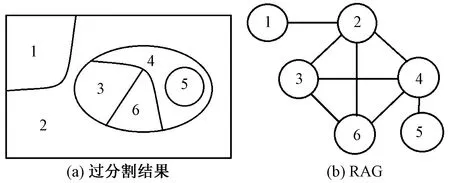
图9 RAG示意图Fig.9 RAG schematic diagram

步骤四根据设置的停止条件判断是否停止合并，如果未达到停止条件，则转到步骤二。

3 基于正交偏光序列图的二次合并操作

由于岩矿石薄片中的矿物颗粒本身的复杂性，通过融合图像的颜色、纹理等特征并不能完全判断相邻的两个目标区域是否属于同一个矿物颗粒，虽然结果得到了很大的改善，但是还是有小部分矿物颗粒会出现一定程度的过分割现象。文献[7]指出，若相邻两目标区域属于同一个矿物颗粒，那么它们的亮度变化趋势相同。根据这个性质引用文献[7]的合并准则对图像进行二次合并操作。

Lab模型是一种基于生理特性的颜色模型，更符合人类视觉，其中L代表亮度，a代表从绿色到红色的分量，b代表从蓝色到黄色的分量，为了更能反映图像明暗程度的差异，将正交偏光序列图像从RGB模型转换到Lab模型，通过比较相邻两目标区域的L分量均值，即亮度均值来判断其是否属于同一个颗粒。

假设两相邻目标区域在图2所示的九个正交偏光角度下的亮度均值序列分别为X=(X1,X2,X3,X4,X5,X6,X7,X8,X9) 和Y=(Y1,Y2,Y3,Y4,Y5,Y6,Y7,Y8,Y9)。采用皮尔森相关系数[18]衡量亮度序列之间的相关性，计算公式如式(10)所示：

(10)

式(10)中：cov(x,y)为两个亮度序列之间的协方差；σx、σy分别为两个亮度序列的标准差；βxy为两个亮度序列之间的皮尔森系数，若βxy=0或接近0则说明两个亮度序列的相关性不高，βxy绝对值越大，则说明两个亮度序列的相关性越高。计算两相邻目标区域的皮尔森相关系数的绝对值作为合并准则，采用2.3节所述的基于RAG的区域合并算法进行二次合并操作。

4 实验结果及分析

为了验证本文算法的有效性，选择一组正交偏光序列图进行实验，并将实验结果与其他算法的实验结果进行比较。

图10 实验结果对比Fig.10 Comparison of experimental results

图7是一组正交偏光序列图的融合图像，图10(a)为按照石油部门标准手工操作得到的矿物颗粒提取分割结果，使用该图作为标准判断分割提取结果的准确度。图10(c)为使用本文算法得到的矿物颗粒提取分割结果，图10(e)为使用基于正交偏光序列图融合图的多阈值分割算法得到的矿物颗粒提取分割结果，图10(g)为使用文献[5]中分割算法得到的矿物颗粒提取分割结果，图10(i)为使用文献[6]中边缘流分割算法得到的矿物颗粒提取分割结果。图10(k)为使用本文算法进行分割，再根据文献[7]提出的合并策略进行合并得到的提取分割结果。图10(b)、图10(d)、图10(f)、图10(h)、图10(j)、图10(l)分别为不同结果图的黑框部分对应的局部区域放大图像。

通过对比可以发现，使用多阈值分割算法会产生大量的颗粒粘连，导致严重的欠分割现象。文献[5]中算法使结果得到了一定的改善，但还是存在一定的欠分割现象，且由于边缘定位不够准确，导致某些颗粒没有被提取出来。文献[6]中的分割算法可以提取出大量的矿物颗粒，但由于该算法对边缘信息过于敏感，会提取到一些不需要的信息，导致一定的误分割和过分割现象。文献[7]中的合并策略没有考虑正交偏光序列图下矿物颗粒的颜色和纹理等特征，所以依然存在部分过分割区域未能合并的现象。

本文算法可以精确定位边缘，能有效处理矿物颗粒相互粘连的现象，通过后续的合并操作，也能有效地抑制过分割现象，对石英、长石等颗粒具有良好的分割提取效果。

5 结论

本文算法以一组正交偏光序列图作为输入，使用改进的FCM算法对每一张正交偏光序列图进行聚类并取边缘，然后叠加边缘并进行精细化处理，再根据亮度信息筛选出目标颗粒，最后使用基于RAG的合并算法根据颜色、纹理及矿物颗粒在不同正交偏光角度下的亮度信息进行区域合并。理论和实验都表明，该算法能精确定位矿物颗粒的边缘，考虑多方面因素的合并操作也能有效抑制过分割现象，具有良好的颗粒分割提取效果，为矿物分类、粒度分析等后续步骤打下坚实的基础。