基于阻抗特性的动力电池系统电磁干扰仿真与测试

张 戟，吕相杰，吕 钰

（同济大学汽车学院，上海201804）

随着电动汽车的迅猛发展，开发出可靠的动力电池系统尤为重要。动力电池系统内部高低电压和大电流同时存在，电磁环境极其复杂，在开发研究前期，尽早发现并解决电池包与电动汽车上其他系统及整车间的电磁干扰问题，是各主机厂和科研院所面临的重要问题。动力电池系统是电动汽车一个重要的高压部件，在高频复杂工况下产生的瞬变电压和电流会影响电池内部及周围环境的电磁场分布，进而改变其扩散效应、极化效应的正常进程，对端电压端电流产生反作用，引起电磁干扰问题。

目前国内外对于汽车电磁兼容性的研究中，几乎都将动力电池从电磁干扰源中排除，对动力电池系统内部的电磁干扰问题不予考虑。在极限运行工况下，电池系统作为供电单元，会随之发生较剧烈的电流电压波动，因此动力电池系统的电磁干扰问题需要进一步的研究。

关于电池包等效模型的研究中，大致可以将其分为三类：电化学模型、电气模型和数学模型。电化学模型是基于电池三维结构、材料、尺寸及内部化学反应等相关参数以大量的非线性微分方程的形式进行构建的，主要用于研究电池内部的电化学反应机理，能够更加准确地预测电池行为，但同时也需要大量的计算资源［1］。数学模型是基于电池包大量数据和经验公式提取的数学符号模型，可以用于预测电池行为，但没有实际的物理意义，在电池包的系统层面常常耗费电池管理系统中的大量时间和空间［2］。贾玉健等人于2011年提出，对于电动汽车电池，可以用等效电路的方式模拟其动态特性，采用电压源、电阻、电容等元器件的串并联，与电路结合能够获取其电气特性［3］。其精度高于数学模型，且具有电气特性；低于电化学模型，但电气模型中使用的元器件适用范围更广。

对于电池的电气模型，一般采用等效电路的表达方式。等效电路有两种构建方式：一种通过充放电测试进行参数辨识的方式得到不同元器件的参数构建等效电路，该方法能够将温度影响纳入到模型中；另一种通过阻抗分析仪等设备，获取电池频域上的阻抗特性，用不同的电子元器件对其进行阻抗匹配拟合，从而构建其等效电路。

对于电驱系统建模，IDIR N.提出分别考虑共模和差模部分的建模方法，差模部分按照电驱正常工作状态搭建，共模部分则对寄生参数加以考虑。用PSPICE进行仿真，仿真结果与实测数据在时域和频域进行了验证［4］。同济大学张戟团队对电驱系统形成了较为全面的电驱系统预测方法，包括基于电机阻抗模型建立、逆变器电流环控制下的传导干扰模型以及按照GB/T 18655-2008搭建的辐射干扰模型［5］。清华大学余绍峰提出采用统计电磁学的方法对燃料电池汽车的电驱系统电磁噪声加以分析，分析结果表明，电磁噪声在时域上近似呈现正态分布，且随电机电压增大而减小［6］。基于传统最大转矩电流比控制，KE L提出一种新型最大转矩电流比控制方法，既考虑了电机参数值的影响，又考虑了电机参数对d-q轴电流导数的影响，能够实现电机在不同工况下的精确控制，同时减少传统最大转矩电流法的计算量［7］。李长红基于公式法最大转矩电流比控制，提出了将d-q轴电流与转矩关系进行线性化处理的工程近似方法，能够提高电机控制速度，减少占用内存，提高响应速度［8］。

由上述研究现状可知，目前的研究大多将电机及逆变器本体与电机控制部分分开考虑，即大多数关于电磁兼容问题的研究中不考虑控制器部分对逆变器信号的影响。本文认为电磁兼容问题大多来源于开关器件的瞬变，而开关器件是受控制器激发而导通或关闭的，因此本文将二者结合，基于电动汽车正常运行工况，建立包括电驱系统在内的整个动力电池系统受控制器激发下的EMI（Electromagnetic Interference）电磁模型，尽量使仿真结果贴合实际。

1 动力电池系统全频段阻抗特性

由于动力电池内部的化学反应及电磁特性并不能直观地展现出来，因此对于电磁兼容方面的研究来说，电池包内部结构可看成黑箱。若给电池包输入端一个扰动信号，那么输出端就会得到一个信号输出。

对一个稳定的线性系统M来说，如果输入激励信号为角频率为ω的正弦波电信号（电压或电流）X，则输出信号也是一个角频率ω的正弦波电信号（电压或电流）Y。Y与X之间的关系如下：

式中：G为频率响应函数，即传递函数。若X为电流信号；Y为电压信号；则G为系统M的阻抗。

本文中所用动力电池单体为LG 60Ah Pouch Cell PE15版本，其正极材料为三元材料，负极为石墨材料。其额定容量为60Ah，标称电压为3.7V。

1.1 电池单体低频（0.01～10kHz）阻抗特性研究

在阻抗定义中，若黑箱系统为稳定的电极系统，角频率为ω的正弦波电流作为输入信号，则此时电极系统的频率响应函数，就是电化学阻抗。

1.1.1 低频阻抗参数提取

低频阻抗参数提取试验平台如图1所示。

图1 电化学阻抗谱测量设备Fig.1 Electrochemical impedance spectrum measuring equipment

LG锂离子电池的电化学阻抗谱测量结果用奈奎斯特图（Nyquist Plot）和波特图（Bode Plot）进行表征，见图2。

图2 锂离子电池电化学阻抗谱测量结果Fig.2 Measurement results of electrochemical impedance spectrum of lithium ion battery

其中，奈氏图中的每个点代表不同的频率，左侧的频率高，右侧的频率低。波特图包括两条曲线，横坐标为频率的对数坐标，纵坐标分别为阻抗的模值和阻抗的相位角。

2.1.2 低频阻抗模型分析

利用电化学阻抗谱研究一个电化学系统的基本思路就是将电化学系统看作是一个等效电路，根据图2中不同频率段的性能表现，可以使用如图3所示的等效电路进行拟合。

图3 锂离子电池低频的等效电路模型Fig.3 Equivalent circuit model of low frequency for lithium ion battery

通过电路仿真软件Zsimpwin对该模型进行拟合验证，拟合参数值如表1所示，拟合结果如图4所示。拟合曲线误差在±3%以内，拟合效果较好。

表1 锂电池电化学阻抗拟合参数Tab.1 Electrochemical impedance fitting parameters of lithium battery

图4 锂离子电池电化学阻抗谱实测和拟合结果Fig.4 Measurement and fitting results of electrochemical impedance spectrum of lithium ion battery

1.2 电池单体中频（10k～1MHz）阻抗特性研究

1.2.1 中频阻抗参数提取

不同频段下的测试原理不同，中频段内的阻抗采用的测量方法为自平衡电桥法。本文采用日置IM3 570阻抗分析仪及配套夹具HIOKI9 262测量中频段（10k～1MHz）阻抗。

搭建好整个测试平台后，中频阻抗特性测量结果如图5所示。由图可见，5个电池单体的阻抗特性基本保持一致。

图5 锂离子电池中频阻抗特性测量结果Fig.5 Measurement results of the intermediate frequency impedance characteristics of lithium ion batteries

1.2.2 中频阻抗模型分析

该部分采用两种建模方式：数学建模和等效电路。通过数学模型可以获取等效电路的参数取值。

（1）数学模型

建立电池高频数学模型根据实测电池阻抗，利用MATLAB进行数据拟合。

对于阻抗幅值-频率特性，采用ployfit函数进行拟合，使所得到的函数值在拟合点处的值与原始点的坐标偏差最小。由于该部分的实测阻抗幅值在常规直线坐标系下呈现斜线形，因此用一阶多项式对阻抗进行拟合，拟合效果如图6a所示。而对于阻抗相位角-频率特性，则采用Exponential指数函数进行拟合，拟合效果如图6b所示。

图6 锂离子电池中频阻抗特性数学模型拟合结果Fig.6 Fitting results of the mathematical model of the lithium-ion battery’s intermediate frequency impedance characteristics

由图可知两者拟合效果较好，式（2）是其函数表达式。

式中：f代表频率；Zm表示阻抗；Thetam表示相位角。

（2）等效电路

在数学模型的基础上，搭建电池单体中频段的等效电路。由上面分析可知，电池单体的阻抗幅值与频率关系呈现线性上升趋势，数学表达式以式（2）表示。则在等效电路中可用电阻Rm和电感Lm的串联表示，由于阻抗幅值较小，因此其值由式（3）近似可求，即

根据式（3）可得 Rm=0.051 6Ω，Lm=416nH。

在Multisim中搭建电池单体的等效电路，仿真阻抗与测试阻抗对比结果如图7所示。

图7 锂离子电池中频阻抗特性等效电路拟合结果Fig.7 Equivalent circuit fitting results of lithium-ion battery intermediate frequency impedance characteristics

由以上分析可知，在中频段（10k～1MHz）范围内，电池单体呈现由阻性到感性的变化。电感特性主要是由电子通过导线以及内部电极缠绕等产生的感抗行为引起的。该部分的等效电路基本与测试阻抗结果相吻合。

1.3 电池单体高频（1M～108MHz）阻抗特性研究

目前国际国内通用的零部件电磁兼容标准规定的传导测试频率范围上限为108MHz，因此本文根据标准规定的频率范围提取电池单体高频（1～108MHz）阻抗参数。

1.3.1 高频阻抗参数提取

高频范围内，网络分析仪法的精确度较高。本文采用日置IM7 587及配套夹具IM9 200测量高频阻抗特性。试验平台及试验过程与中频段测量保持一致。

同样，搭建好整个测试平台后，高频阻抗特性测量结果如图8所示。

图8 锂离子电池高频阻抗特性测量结果Fig.8 Measurement results of high-frequency impedance characteristics of lithium-ion batteries

由相角特性可以看出，锂电池单体在100MHz附近相角由正值变为负值，表示其由感性变为容性。在高频段锂电池的电感、电容特性如图9所示。

由图9所示，不同锂离子电池单体在高频下的阻抗特性存在差异，因此选取5个电池单体的平均值进行后续仿真及分析。

图9 锂电池单体的寄生电感和寄生电容频谱曲线Fig.9 Spectral curves of the parasitic inductance and parasitic capacitance of a lithium battery cell

1.3.2 高频阻抗模型分析

由图8a电池单体的阻抗特性可以看出，高频下电池存在两个谐振点波峰，分别为72.2MHz对应幅值为397ohm和97.4MHz对应幅值为5 330ohm。因此考虑采用两阶LC并联回路模拟其谐振点。

RLC并联电路的阻抗为

谐振频率如下：

式中：X为复阻抗；R为电阻；L为电感；C为电容。如前所述，电池单体的谐振频率分别为72.2MHz和97.4MHz，由式（5）可知

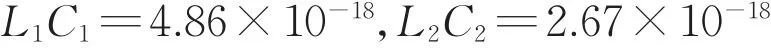
此外，由式（4）可知，在谐振点处阻抗为纯电阻，与电感L1，L2和电容C1，C2无关。如前所述，谐振波峰值分别为397ohm和5 330ohm，因此为了便于后期计算拟合，可以假设R1=397Ω，R2=5330Ω。

为确定L1和L2的取值，可以分别取频率为70和100MHz处的幅值代入计算，可得

由 此 可 得 ，L1=0.01μH，L2=0.2μH，C1=486pF，C2=13.35pF。

采用Multisim软件对阻抗进行拟合仿真，如图10所示。绿色的探针用以监测电路电压和电流，从而计算阻抗。采用AC仿真方式对1～108MHz进行扫频仿真。

仿真与测试结果对比如图11所示。

由图11可知，锂离子电池单体在高频时从感性逐渐变为容性，在97.4MHz附近阻抗值达到最大值，电路拟合与测试结果基本一致，可以用于后续电路仿真。

将锂离子电池单体的低频、中频和高频数据组合在一起进行全频段阻抗拟合仿真。以图10的等效电路对全频段阻抗特性进行拟合，拟合结果如图12所示。

图10 锂离子电池高频阻抗等效电路Fig.10 High-frequency impedance equivalent circuit of lithium-ion battery

由图12可见，在全频段内等效电路拟合的阻抗特性与测试结果较为一致。此外，本文所研究电池包电池单体之间通过低压线束连接，而电池模组之间通过BUSBAR连接。考虑到BUSBAR通常会呈现一定的阻抗特性，影响电池包的电流及电压分布，因此BUSBAR的阻抗也是电磁兼容性能研究中不可忽略的一部分。

图11 锂离子电池高频阻抗特性等效电路拟合结果Fig.11 Equivalent circuit fitting results of high-frequency impedance characteristics of lithium-ion batteries

图12 锂离子电池全频阻抗特性等效电路拟合结果Fig.12 Fitting result of equivalent circuit of full-frequency impedance characteristic of lithium ion battery

1.4 BUSBAR的阻抗特性研究

对于BUSBAR采用日置IM7587阻抗分析仪及其配套夹具IM9200测量其1～108MHz的阻抗特性，测试过程如图13所示，阻抗特性的测量数据含有两个波峰。产生波峰的频率点分别为f=74.7MHz，Z=2 409.35Ω和f=82MHz，Z=1 855.03Ω。同样采用1.3节的阻抗拟合方法对BUSBAR的阻抗特性进行等效电路拟合。最终确定等效电路的拟合参数如图14所示。

图13 BUSBAR高频阻抗特性测试图Fig.13 BUSBAR high frequency impedance characteristic test chart

图14 BUSBAR高频阻抗等效电路Fig.14 BUSBAR high-frequency impedance equivalent circuit

将BUSBAR的阻抗特性仿真和实测结果进行对比，如图15所示。可见其阻抗特性在幅值和相位角上存在一定误差，但基本上呈现走向一致的趋势。

2 电驱动控制系统建模

电驱系统作为动力电池系统EMI的主要干扰源，在不同控制方式下呈现出不同的电流及电压变化情况。本文电驱系统为90kW永磁同步驱动系统，其仿真模型主要包含：空间矢量脉冲宽度调制（SVPWM）模块、DC/AC逆变器、控制器算法等几部分。

图15 BUSBAR高频阻抗特性等效电路拟合结果Fig.15 BUSBAR high-frequency impedance characteristic equivalent circuit fitting results

2.1 空间矢量脉冲宽度调制

对于三相三桥臂逆变器，每个桥臂有上下两个开关管，开关管有两种状态：开启和关闭，上下开关管的状态相反。故三相三桥臂逆变器的开关状态有23即8种，如图16所示。

图16 电压空间矢量图Fig.16 Voltage space vector

用Uα和Uβ表示合成矢量Uout在α、β轴上的分量，令

再定义3个变量A、B、C，通过分析可得若Uref1＞0，则A=1，否则A=0；若Uref2＞0，则B=1，否则B=0；若Uref3＞0，则C=1，否则C=0；令N=4C+2B+A，则可以得到N与扇区的关系，如表2所示。

表2 N与扇区的对应关系Tab.2 The correspondence between N and sectors

确定扇区矢量切换点，搭建的Simulink模块如图17所示。

图17 切换时间Tcm1，Tcm2和Tcm3的计算Fig.17 Calculation of switching timeTcm1，Tcm2and

使用三角波与所获取的信号进行比较，Repeating Sequence模块的频率与PWM波的频率保持一致为10kHz，幅值为周期的一半0.000 05，由此可以获得逆变器使能端的六路信号，该模块如图18所示。在控制部分的采样速率与IGBT的频率保持一致，其他部分设置为后续仿真所需要的精度。因此使用RT模块进行采样速率控制，可以提高仿真速度。

图18 产生PWM波Fig.18 Generate PWM wave

综上所述，SVPWM部分的仿真模型如图19 所示。

图19 SVPWM波形产生模块Fig.19 SVPWM waveform generation module

2.2 最大转矩电流比控制

如前所述，凸极式永磁同步电机的电枢电流经过坐标变换后，电机的电磁转矩表达如下：

设Υ为电枢电流空间矢量与直轴位置的相位角，可得

则电磁转矩为

由此可得

式中：Pn是电机极对数；Ld和Lq是电感分量；φf是磁链；id,iq为电流分量；is为定子电流矢量幅值。

电流is的幅值保持恒定，则单位电流电磁转矩最大值时可得∂f(γ)/∂γ=0，进而可得

解得

将式（12）代入式（8）可得

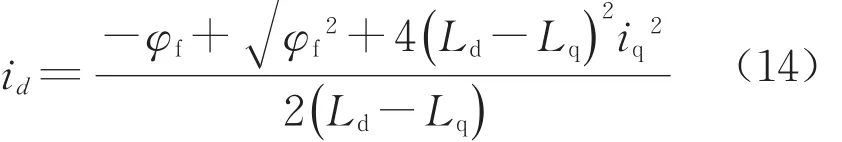
根据id和iq的关系，用iq表示id，得

本文考虑采用查表法对该部分进行建模。电磁转矩作为转矩电流关系模块的输入，转矩电流关系模块的输出作为id、iq的给定输入，最后再经过电流调节器进而控制SVPWM模块。

综上所述，永磁同步电机的最大转矩电流比控制框图见图20。

图20 PMSM最大转矩电流比控制原理Fig.20 PMSM maximum torque current ratio control principle

3 基于阻抗特性的动力电池系统EMI仿真与测试

3.1 工况模拟

依据GB/T 18387—2008中的工况设置，主要研究的工况为起步加速到70km·h-1以及从70km·h-1减速制动到停止的过程，后续的实车行驶测试都按照该工况进行。根据所需工况模拟电机转矩和转速，进行包括电池包在内的电驱系统控制仿真。

首先获取汽车车速的运行状态，如图21所示。

图21 加减速工况下的车速随时间变化Fig.21 Change of vehicle speed with time under acceleration and deceleration conditions

电动机的外特性如图22所示，电动机的输出转矩为

图22 电动机的外特性曲线Fig.22 External characteristic curve of the motor

电动汽车的驱动力为

式中：Ts为电动机转矩；it为传动系总传动比；ηt为传动系统的机械效率；R为车轮半径。在恒功率区域，电动汽车的驱动力是电机转速的函数。滚动阻力Ff、Fw、Fj、空气阻力和加速阻力的计算如下：

汽车行驶方程式如下：

由式（19）可知，当电机到达恒功率区域时，电机转矩与汽车行驶加速度成一次线性关系。结合电机启动到加速过程中由恒转矩到恒功率的变化过程，可以得到转矩与时间的关系如图23所示。

图23 电动机输入转矩曲线Fig.23 Motor input torque curve

由图23可知，在0～6s的时间内电机启动，转矩呈现梯形上升；在6～8s时间内电机为恒转矩的运行状态，8s之后，电机工作在恒功率区域内，与汽车车速成正相关。对于电机转速，与汽车车速成正比。计算如下：

式中：u为汽车车速；it为传动比；R是轮胎半径；n是电机转速。

与电机转矩对应，当电机转矩结束恒功率区域时，电机转速达到额定转速4 000r·min-1。至此可确定电机的机械角转速随时间变化的曲线如图24所示。

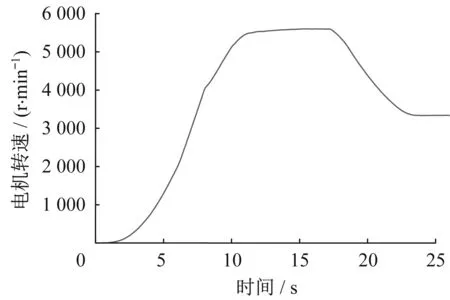
图24 电动机输入转速曲线Fig.24 Motor input speed curve

对于整个电驱系统，包括DC/AC信号触发和永磁同步电机反馈环在内的控制部分如图25所示。

图25 PMSM最大转矩电流比控制模型Fig.25 PMSM maximum torque current ratio control model

综上所述，结合前文电池包阻抗模型、全桥DC/AC模块、电机模块以及控制部分，动力电池系统的模型如图26所示。

其中，图26中的控制部分为图25所示逆变器信号和电机控制部分，电机的输出RT模块用于控制离散时间变量，使采样时间间隔与逆变器的周期保持一致，以提高仿真速度。仿真所得电机转速和转矩如图27所示。

对比图27和图23～图24可知，仿真的电机转速和转矩结果与给定电机转矩和转速几乎保持一致。也就是说在最大转矩电流比法的控制下，电机的输出转矩和转速基本完全响应加减速工况下的输入转矩和转速，可见该电驱系统仿真模型是准确的。

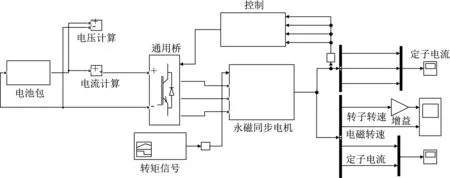
图26 动力电池系统电磁仿真模型Fig.26 Electromagnetic simulation model of power battery system

图27 电驱系统仿真电机输出转矩和转速结果Fig.27 The output torque and speed of the simulated motor of the electric drive system

3.2 实车行驶测试验证

为了验证研究的电池包及电驱系统模型的准确性，需要在实车上进行行驶试验。

图28a为大众凌度样车，图28b为数据采集端，PC端的CANoe软件通过USB与CANoe硬件相连，CANoe硬件通过光纤与电动车上的两路CAN相连。电池包内部出现电磁干扰时，电驱系统及逆变器模块出现剧烈的电流电压变化。为模拟电池包内部电磁干扰的情况，实车运行工况为从0加速到70km·h-1再减速到0。

图28 电动汽车实车工况数据采集布置总图Fig.28 General layout of data collection for electric vehicle actual vehicle operating conditions

将实车上采集到的车速随时间变化情况进行解码，通过动力学计算得到电机转矩及转速的变化情况，作为电驱系统的输入，模拟仿真得到电池包两端母线电流。同样对电池包两端母线电流进行解码，由此可得到实车上的电池包母线总电流，将该电流与前述仿真电流结果进行对比，如图29所示。

图29 电池包两端母线电流仿真与测试对比Fig.29 Comparison of current simulation and test on both sides of the battery pack

由图29可知，仿真和实测电流基本保持一致，验证了该干扰源模型的准确性。加速时，电池包处于放电状态，电流为正；刹车时，电池包回收制动能量，电流为负，电池包处于充电状态。起步达到最高车速以及开始制动时，母线电流波动较大，容易引起电磁干扰问题。实车测试所得电流曲线为仿真电流结果的包络，这主要是因为CAN总线的数据传输速率最大为500kbit·s-1，采用CANoe采集总电流数据时采样精度约为100kHz，而逆变器全桥电路的开关频率为10kHz，因此CANoe采集到的数据中未体现IGBT关断的瞬间；而在仿真模型中，采样时间间隔设置为最大10ns，因此在一个IGBT的开关周期内，可以采集约1 000次数据，因此能够体现开关器件的开通和关断状态。实测结果和仿真结果在包络上一致，说明模型精度能够接受。

4 结论

考虑到纯电动汽车上主要的电磁干扰源为电驱系统，而电池包又直接与电驱系统相连，本文对包括电池包、电机、电机控制器在内的整个动力电池系统干扰源进行了建模仿真，并通过实车测试验证了仿真模型的准确性。

电池包采用搭建的全频段等效电路阻抗模型，电机采用三对极凸极式永磁同步电机，采用查表法最大转矩电流比进行控制，空间矢量脉冲宽度调制产生逆变器6路IGBT的使能信号。电驱系统运行在加减速工况下，系统模型的输入为电机转矩和转速，在仿真模型中监测电池包直流母线上的总电流。

为验证该模型的准确性，同样采集实车母线总电流，用DBC对实车数据进行解码，将实测电流与仿真模型所得电流进行对比，发现在加（减）速度较大的区间范围内，电流的波动较强烈，容易引起动力电池系统电池单体上的电压波动，仿真数据与实测数据一致，仿真结果可以对动力电池系统母线上的总电流干扰有一个准确的预测。